Fencing material is sold at \(\text{R}\,\text{95,20}\) per metre. How much is the fencing material going to cost him?
\(\text{90}\) \(\times\) \(\text{R}\,\text{95,20}\) = \(\text{R}\,\text{8 568,00}\)
|
Previous
5.1 Introduction and key concepts
|
Next
5.3 Measuring mass or weight
|
We can estimate some lengths and distances using approximate values for measurements. For example, one metre is approximately the length from your shoulder to your fingertips, if you stand with your arm outstretched. A metre is also approximately the distance of one large step or jump.
Whilst estimating length and distance can be useful, we often need to know exactly how long something is. To measure accurately, we use measuring instruments. Some examples are given in the table below:
| A ruler is usually has centimetre and millimetre units on it. They are most commonly \(\text{15}\) \(\text{or}\) \(\text{30}\) \(\text{cm}\) long. A ruler could be used to measure the length of small tin, or the length of a piece of paper, for example. |
| A measuring tape has centimetre and metre units marked on it. Measuring tapes are useful for measuring lengths of cloth, or large household objects like furniture and rooms. |
| The length around the circle (the circumference) of a trundle wheel is \(\text{1}\) \(\text{m}\). When it is rolled across the floor, it makes a 'click' sound for every full rotation of the circle or \(\text{1}\) metre measured. Trundle wheels may be used to measure the length of a classroom, a corridor or a field, for example. |
| An odometer (pronounced o-dom-e-ter) is a measuring instrument used in cars to measure the distance travelled. The displayed number increases by \(\text{1}\) unit for every kilometre the car travels. In the odometer on the left, this car has driven \(\text{100 000}\) \(\text{km}\) in total. |
Carl needs to measure the width of a window, to find out how much material he needs to buy to make a curtain. The curtain material costs \(\text{R}\,\text{55}\) per metre.

Carl estimates the width of the window (using his arm) to be \(\text{1,9}\) metres wide. If Carl goes to the shop with this estimate:
Carl decides to double-check his estimated measurement before he buys the material and uses his tape measure to accurately measure the width of the window. He determines that the window is actually \(\text{2,2}\) \(\text{m}\) wide.
This example shows us that while being able to estimate length is useful, in some situations it's important to be accurate! If Carl had used his estimated measurement instead of his tape measure, his cost estimate would have been too low and his curtain would have been too short to cover his window.

Liz sews dresses for little girls. The material costs \(\text{R}\,\text{89,50}\) per metre and she needs \(\text{2}\) metres of material to make a dress for a \(\text{4}\) year old; \(\text{2,5}\) metres to make a dress for a \(\text{7}\) year old and \(\text{3}\) metres to make a dress for \(\text{10}\) year old. The embroidery cotton costs \(\text{R}\,\text{12,55}\) for a roll of \(\text{3}\) metres. She uses \(\text{2}\) rolls of cotton per dress.
Length of one roll of cotton \(\times\) \(\text{2}\) = \(\text{3}\) \(\text{m}\) \(\times\) \(\text{2}\) = \(\text{6}\) \(\text{m}\), or \(\text{600}\) \(\text{cm}\) per dress.
Mr. Madikiza has just finished building a new house. He measured the distance around his yard and found it to be \(\text{90}\) \(\text{m}\).

Fencing material is sold at \(\text{R}\,\text{95,20}\) per metre. How much is the fencing material going to cost him?
\(\text{90}\) \(\times\) \(\text{R}\,\text{95,20}\) = \(\text{R}\,\text{8 568,00}\)
Suppose he has to put a pole after every \(\text{1,5}\) \(\text{m}\). How many poles will he have to buy?
\(\text{90}\) \(\div\) \(\text{1,5}\) = \(\text{60}\). He will need \(\text{60}\) poles.
If the fencing poles cost \(\text{R}\,\text{65}\) each, calculate the total costs of the poles alone.
\(\text{60}\) \(\times\) \(\text{R}\,\text{65}\) = \(\text{R}\,\text{3 900,00}\)
Calculate the total cost of fencing the yard.
\(\text{R}\,\text{8 568,00}\) + \(\text{R}\,\text{3 900,00}\) = \(\text{R}\,\text{12 468,00}\)
Jenny has started a decorating business and has a contract to provide decor at a wedding reception.

The tables used at this wedding are rectangular with a length of \(\text{3}\) \(\text{m}\) and a width of \(\text{1}\) \(\text{m}\). The fabric she plans to use for the tablecloth costs \(\text{R}\,\text{75}\) per metre (but can be bought in lengths smaller than a metre) and is sold in rolls that are \(\text{1,4}\) \(\text{m}\) wide. The bride and groom want the tablecloths to hang at least \(\text{20}\) \(\text{cm}\) over the edges of the tables. Calculate the cost of the cloth for each table. 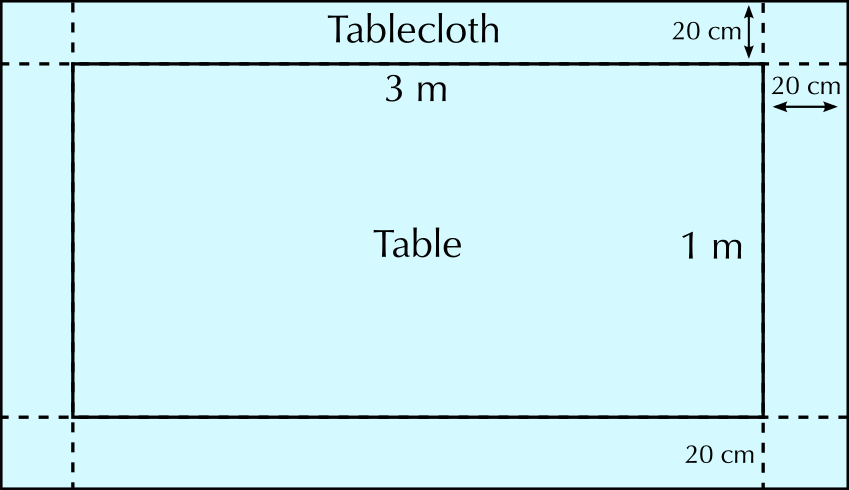
The cloth is the same width (\(\text{1}\) \(\text{m}\) + \(\text{20}\) \(\text{cm}\) + \(\text{20}\) \(\text{cm}\)) as the fabric sold. She will therefore need \(\text{3,4}\) metres of material to cover one table. \(\text{3,4}\) \(\text{m}\) \(\times\) \(\text{R}\,\text{75,00}\) = \(\text{R}\,\text{225,00}\)
If there are \(\text{15}\) tables at the wedding, calculate how much she is going to spend on tablecloths alone.
\(\text{R}\,\text{225,00}\) \(\times\) \(\text{15}\) tables = \(\text{R}\,\text{3 825,00}\)
|
Previous
5.1 Introduction and key concepts
|
Table of Contents |
Next
5.3 Measuring mass or weight
|