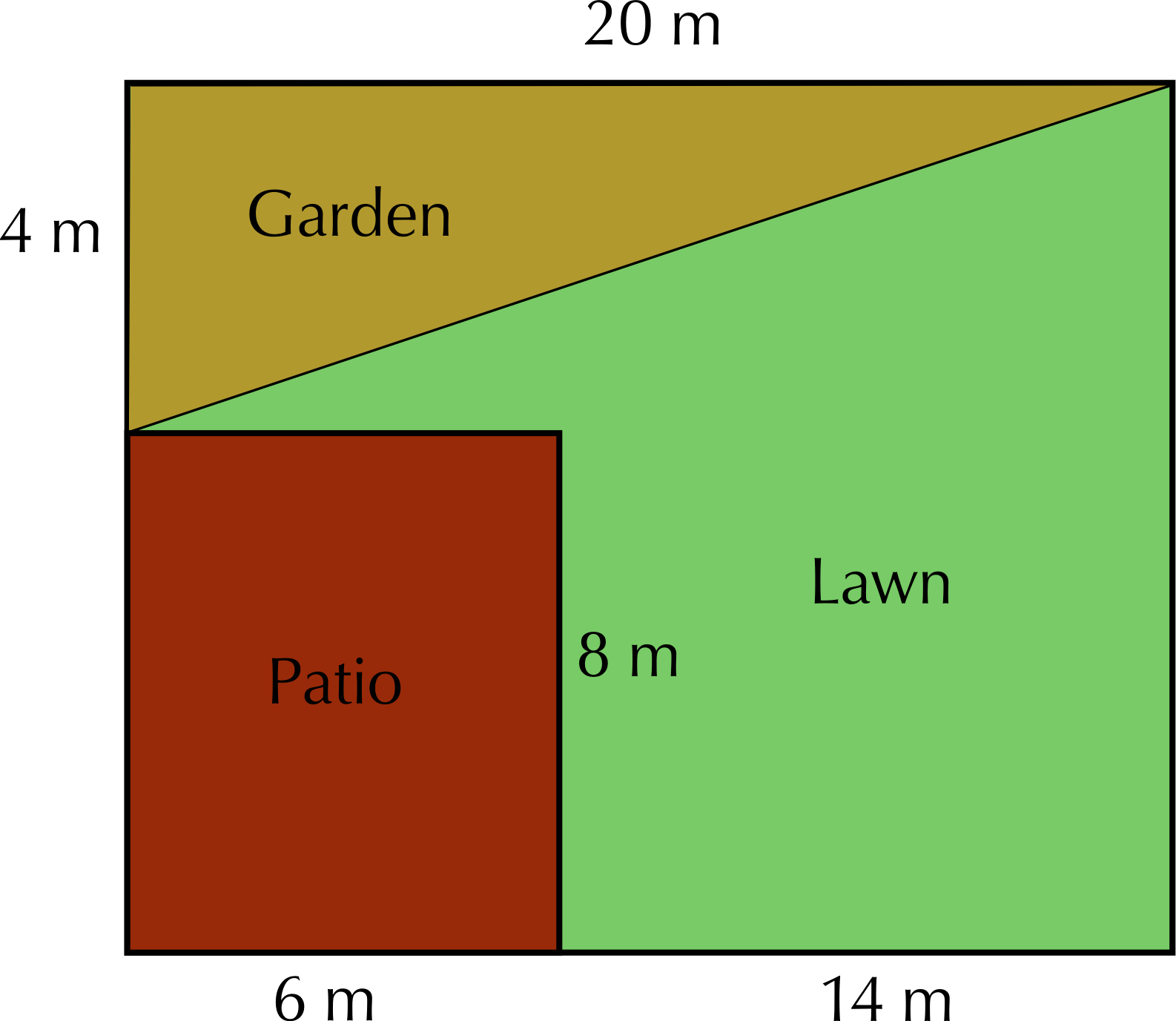
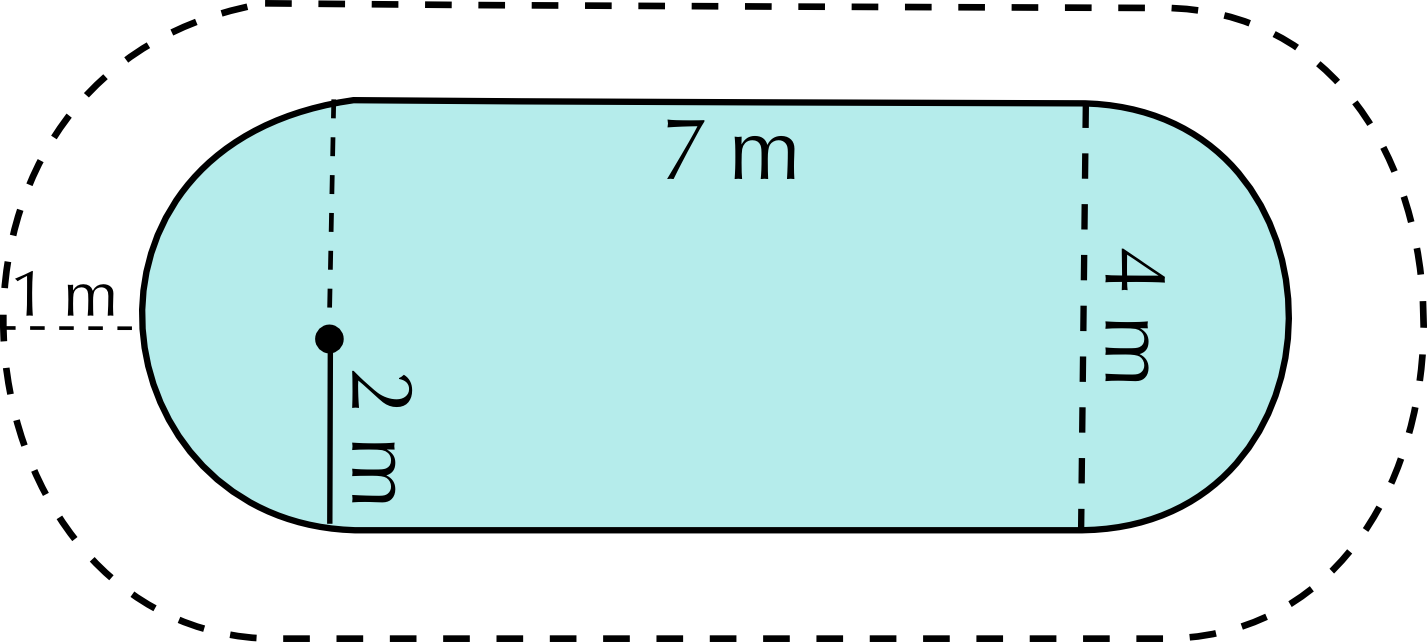
Mr Dlamini is concerned that his dog will try to climb into the fish pond once it's built. He will need to put a fence around the fish pond. He has still not decided which style of fish pond he wants to build. He decides to get quotes from a fencing company called “Fence-Me-In”. They give him the following information:
- Labour costs: \(\text{R}\,\text{549,99}\) for the whole project
- \(\text{1}\) metre of fencing costs \(\text{R}\,\text{29,99}\).
Calculate the total cost for each style of pond.
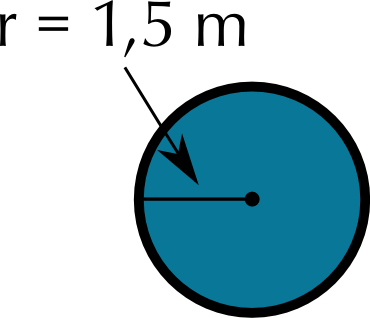
Pond shape 1 (circle): cost = Labour + fencing price \(\times\) perimeter = \(\text{R}\,\text{549,99}\) + (\(\text{R}\,\text{29,99}\))(\(\text{2}\pi \times\) \(\text{1,5}\) \(\text{m}\)) = \(\text{R}\,\text{549,99}\) + R(\(\text{29,99}\))(\(\text{9,426}\) \(\text{m}\)) = \(\text{R}\,\text{549,99}\) + \(\text{R}\,\text{282,69}\) = \(\text{R}\,\text{832,68}\).
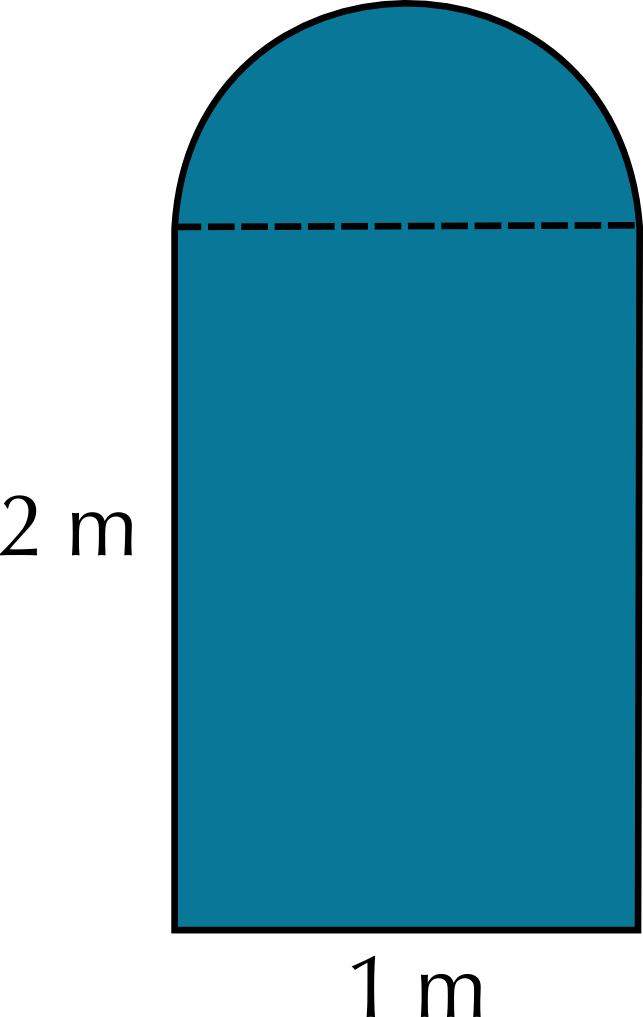
Pond shape 2: Cost = Labour + fencing price \(\times\) perimeter = \(\text{R}\,\text{549,99}\) + (\(\text{R}\,\text{29,99}\))(\(\text{2}\) \(\text{m}\) + \(\text{1}\) \(\text{m}\) + \(\text{2}\) \(\text{m}\) + \(\frac{\text{1}}{\text{2}} \times \text{2} \times \pi \times\) \(\text{1}\) \(\text{m}\)) = \(\text{R}\,\text{549,99}\) + (\(\text{R}\,\text{29,99}\))(\(\text{5}\) \(\text{m}\) + \(\text{3,142}\) \(\text{m}\)) = \(\text{R}\,\text{549,99}\) + \(\text{R}\,\text{244,18}\) = \(\text{R}\,\text{794,17}\)
Based on your answers to Questions 2 c) and d), which style of fish pond do you think Mr Dlamini should choose? Give reasons for your answer.
Learner-dependent answer, but based on his concern about the size of the pond he should choose the second design - it's cheaper to fence too.