2.1 Introduction
|
Previous
End of chapter exercises
|
Next
2.2 Revision of exponent laws
|
Chapter 2: Exponents
2.1 Introduction (EMAS)
- Content covered in this chapter includes the laws of exponents from grade 9 and simplifying expressions with exponents as well as solving simple exponential equations.
- The content in this chapter will be used in exponential equations later on as well as in grade 11 for financial calculations.
- Note that the rational exponent law is not covered in this chapter, this is only introduced in grade 11.
Exponential notation is a short way of writing the same number multiplied by itself many times. This is very useful in everyday life. You may have heard someone describe the size of an area in square metres or square kilometres. For example, the largest radio telescope in the world is being built in South Africa. The telescope is called the square kilometre array, or SKA. This is because the telescope will occupy an area of \(\text{1}\) kilometre by \(\text{1}\) kilometre or \(\text{1}\) kilometre squared.

Exponents are also very useful to describe very large and very small numbers. For example, the SKA will be detecting incredibly weak signals from objects which are so far away that to write out the strength of the signal or the number of kilometres away in full would be impractical. Outside of astronomy, exponents are used by many other professions such as computer programmers, engineers, economists, financial analysts, biologists and demographers.
If you want to know more about how exponents are used then take a look at the following presentation.
You have already been introduced to exponents and exponent laws in previous grades. Remember that exponents can also be called indices or powers. Exponential notation is as follows:
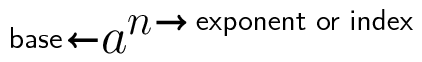
For any real number \(a\) and natural number \(n\), we can write \(a\) multiplied by itself \(n\) times as: \({a}^{n}\).
Remember the following identities:
-
\({a}^{n} = a \times a \times a \times \cdots \times a \enspace \left(n \text{ times}\right) \enspace \left(a\in \mathbb{R}, n\in \mathbb{N}\right)\)
-
\({a}^{0}=1 \quad \left(a\ne 0 \text{ because }{0}^{0} \text{ is undefined}\right)\)
-
\({a}^{-n}=\dfrac{1}{{a}^{n}} \quad \left(a\ne 0 \text{ because }\dfrac{1}{0} \text{ is undefined}\right)\)
- Similarly, \(\dfrac{1}{a^{-n}} = a^{n}\)
Interested in finding out why raising a real number to the power of zero is one? Try work it out for yourself. If you get stuck, you can see an example of how to show this is true at this link.
Look at the following examples to see these identities in action:
-
\(3\times 3={3}^{2} = 9\)
-
\(5\times 5\times 5\times 5= {5}^{4}\)
-
\(p\times p\times p={p}^{3}\)
-
\({\left({3}^{x}\right)}^{0}=1\)
-
\({2}^{-4}=\dfrac{1}{{2}^{4}}=\dfrac{1}{16}\)
-
\(\dfrac{1}{{5}^{-x}}={5}^{x}\)
If your final answer is easier to work out without a calculator, then write it out in full - not in exponential notation, as in examples 1 and 5.
It is convention to write your final answer with positive exponents.
In this chapter, we will revise the exponent laws and use these laws to simplify and solve more complex expressions and equations.
To revise what exponents are you can watch the following video.
|
Previous
End of chapter exercises
|
Table of Contents |
Next
2.2 Revision of exponent laws
|
