Furniture store opening special:
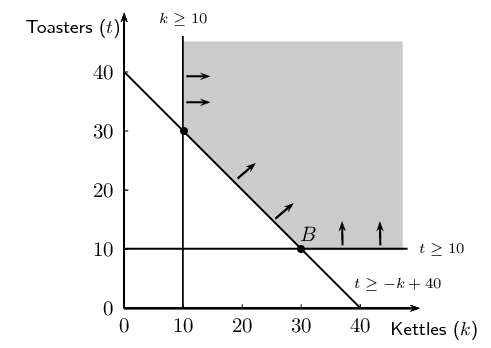
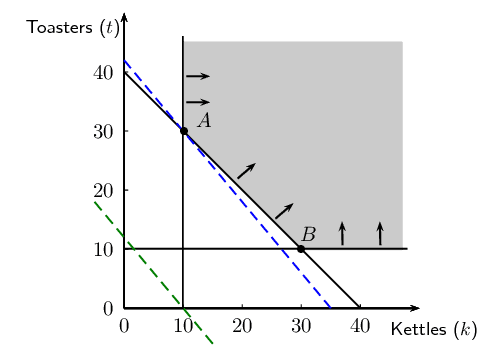
As part of their opening special, a furniture store has promised to give away at least \(\text{40}\) prizes with a total value of at least \(\text{R}\,\text{4 000}\). They intend to give away kettles and toasters. They decide there will be at least \(\text{10}\) units of each prize. A kettle costs the company \(\text{R}\,\text{120}\) and a toaster costs \(\text{R}\,\text{100}\).
Determine how many of each prize will represent the cheapest option for the company. Calculate how much this combination of kettles and toasters will cost.
Use a suitable strategy to organise the information and solve the problem.
In this situation there are two variables that we need to consider: let the number of kettles produced be \(K\) and let the number of toasters produced be \(T\).
Write down a summary of the information given in the problem so that we consider all the different components in the situation.
\[\begin{array}{l@{\;}l} \text{minimum number for } K &= 10 \\ \text{minimum number for } T &= 10 \\ \text{cost of } K &= \text{R}\,\text{120} \\ \text{cost of } T &= \text{R}\,\text{100} \\ \text{minimum number of prizes } &= 40 \\ \text{minimum total value of prizes } &= \text{R}\,\text{4 000} \end{array}\]Use the summary to draw up a table of the number of kettles and toasters that are needed. We will consider multiples of 5 to simplify the calculations:
| \(K\) | \(T\) | ||||
| \(\text{10}\) | \(\text{15}\) | \(\text{20}\) | \(\text{25}\) | \(\text{30}\) | |
| \(\text{10}\) | \((10;10)\) | \((10;15)\) | \((10;20)\) | \((10;25)\) | \((10;30)\) |
| \(\text{15}\) | \((15;10)\) | \((15;15)\) | \((15;20)\) | \((15;25)\) | \((15;30)\) |
| \(\text{20}\) | \((20;10)\) | \((20;15)\) | \((20;20)\) | \((20;25)\) | \((20;30)\) |
| \(\text{25}\) | \((25;10)\) | \((25;15)\) | \((25;20)\) | \((25;25)\) | \((25;30)\) |
| \(\text{30}\) | \((30;10)\) | \((30;15)\) | \((30;20)\) | \((30;25)\) | \((30;30)\) |
We need to have at least \(\text{40}\) kettles and toasters together.
With this limitation, we are able to eliminate some of the combinations in the table where \(K + T < 40\):
| \(K\) | \(T\) | ||||
| \(\text{10}\) | \(\text{15}\) | \(\text{20}\) | \(\text{25}\) | \(\text{30}\) | |
| \(\text{10}\) | \(\cancel{(10;10)}\) | \(\cancel{(10;15)}\) | \(\cancel{(10;20)}\) | \(\cancel{(10;25)}\) | \((10;30)\) |
| \(\text{15}\) | \(\cancel{(15;10)}\) | \(\cancel{(15;15)}\) | \(\cancel{(15;20)}\) | \((15;25)\) | \((15;30)\) |
| \(\text{20}\) | \(\cancel{(20;10)}\) | \(\cancel{(20;15)}\) | \((20;20)\) | \((20;25)\) | \((20;30)\) |
| \(\text{25}\) | \(\cancel{(25;10)}\) | \((25;15)\) | \((25;20)\) | \((25;25)\) | \((25;30)\) |
| \(\text{30}\) | \((30;10)\) | \((30;15)\) | \((30;20)\) | \((30;25)\) | \((30;30)\) |
These combinations have been excluded as possible answers.
We can express the minimum cost as: \(C = \text{120}(K) + \text{100}(T)\).
By substituting the different combinations for \(K\) and \(T\), we can find the value that gives the minimum cost.
| \(K\) | \(T\) | ||||
| \(\text{10}\) | \(\text{15}\) | \(\text{20}\) | \(\text{25}\) | \(\text{30}\) | |
| \(\text{10}\) | \(\cancel{(10;10)}\) | \(\cancel{(10;15)}\) | \(\cancel{(10;20)}\) | \(\cancel{(10;25)}\) | \((15;30) \Rightarrow \text{R}\,\text{4 200}\) |
| \(\text{15}\) | \(\cancel{(15;10)}\) | \(\cancel{(15;15)}\) | \(\cancel{(15;20)}\) | \((15;25) \Rightarrow \text{R}\,\text{4 300}\) | \((15;30) \Rightarrow \text{R}\,\text{4 800}\) |
| \(\text{20}\) | \(\cancel{(20;10)}\) | \(\cancel{(20;15)}\) | \((20;20) \Rightarrow \text{R}\,\text{4 400}\) | \((20;25) \Rightarrow \text{R}\,\text{4 900}\) | \((20;30) \Rightarrow \text{R}\,\text{5 400}\) |
| \(\text{25}\) | \(\cancel{(25;10)}\) | \((25;15) \Rightarrow \text{R}\,\text{4 500}\) | \((25;20) \Rightarrow \text{R}\,\text{5 000}\) | \((25;25) \Rightarrow \text{R}\,\text{5 500}\) | \((25;30) \Rightarrow \text{R}\,\text{6 000}\) |
| \(\text{30}\) | \((30;10) \Rightarrow \text{R}\,\text{4 600}\) | \((30;15) \Rightarrow \text{R}\,\text{5 100}\) | \((30;20) \Rightarrow \text{R}\,\text{5 600}\) | \((30;25) \Rightarrow \text{R}\,\text{6 100}\) | \((30;30) \Rightarrow \text{R}\,\text{6 600}\) |
We are looking for a pair of values that give the minimum cost. We can easily check the non-multiples of 5 for kettles and toasters to confirm that \(\text{10}\) kettles and \(\text{30}\) toasters meet the minimum cost.
For example if \(\text{11}\) kettles and \(\text{29}\) toasters are given away, the cost will be \(\text{R}\,\text{4 220}\). And if \(\text{12}\) kettles and \(\text{28}\) toasters are given away, the cost will be \(\text{R}\,\text{4 340}\).
The minimum cost of \(\text{R}\,\text{4 000}\) can be obtained if \(\text{10}\) kettles and \(\text{30}\) toasters are given away. This will result in a cost of \(\text{R}\,\text{4 200}\).