6.7 Chapter summary

• An algebraic expression indicates a sequence of calculations that can also be described in words or with a flow diagram.
• In an algebraic expression, the unknowns are called variables. They stand in the place of numbers until we decide what numbers we want to put in their place. For example, given the expression \(3x - 5y\), the variables are \(x\) and \(y\).
• A coefficient is a number that you multiply by a variable. We usually place the coefficient in front of the variable.
• A constant is a number (without a variable) that is added or subtracted.
• An exponent is a number or variable that shows us how many factors there are.
• In an expression that can be written as a sum, the different parts of the expression are called the terms of the expression. For example, \(3x\), \(2z\) and \(y\) are the terms of the expression \(3x + 2z + y\).
• An expression can have like terms or unlike terms, or both.
• Like terms are terms that have the same variable(s) raised to the same power. For example, the terms \(3x\) and \(2x\) are examples of like terms, but the terms \(2x\) and \(2z\) are unlike terms.
• Terms are like terms if two things are true:
  • the terms have the same variable or variables (or both terms have no variable)
  • the variables have the same exponents.
• Terms are separated by addition and subtraction symbols, and joined into one by multiplication symbols, division symbols, and brackets.
• To evaluate an expression, we must:
  • separate it into terms
  • simplify each term (if needed)
  • add or subtract from left to right.
• When working with algebraic expressions that contain fractions, it is always important to check whether there are variables in the denominator. An expression is undefined when we try to divide by zero, in other words, when zero is in the denominator of a fraction.
• When working with square roots, it is important to pay attention to the variables under the square root. An expression is undefined when we try to take a square root of a negative number.
• The distributive law of multiplication over addition (or subtraction) states that:

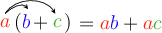
• The commutative law states that the order in which we add or multiply numbers does not change the answer: \(a + b = b + a\) and \(ab = ba\).
• The associative law states that the way in which we group three or more numbers when adding or multiplying does not change the answer: \((a + b) + c = a + (b + c)\) and \((ab)c = a(bc)\).