8.6 Chapter summary
- The algebraic expressions that involve division are called algebraic fractions. The rules that govern operations with fractions also apply to algebraic fractions.
- Here are some important things to remember about fractions:
- When multiplying fractions, we multiply the numerators and multiply the denominators: \(\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\). So, we can also go the opposite way to separate the fraction when we have a fraction with only products: \(\frac{a \times c}{b \times d} = \frac{a}{b} \times \frac{c}{d}\)
- When adding (or subtracting) fractions, if the denominators are the same, then we can add (or subtract) the numerators: \(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\). So, we can also go the opposite way to separate the fraction when we have a fraction with addition (or subtraction) in the numerator: \(\frac{a + b}{c} = \frac{a}{c} + \frac{b}{c}\).
- To simplify an expression:
- Separate it into terms. Terms are separated by addition and subtraction symbols, and joined into one by multiplication and division symbols, and brackets.
- Simplify each term (if needed).
- Add or subtract like terms from left to right (if possible).
- To simplify the algebraic expressions with roots:
- Square roots, e.g. \(\sqrt{16x^{2}}\). Expand the power, then group the bases into two equal groups. \(\sqrt{16x^{2}} = \sqrt{(4x) \times (4x)} = \sqrt{(4x)^{2}} = 4x\)
- Cubic roots: e.g. \(\sqrt[3]{t^{6}}\). Expand the power, then group the bases into three equal groups. \(\sqrt[3]{3t^{2} \times 3t^{2} \times 3t^{2}} = \sqrt[3]{\left( 3t^{2} \right)^{3}} = 3t^{2}\)
- Recall the distributive property of multiplication over addition (or subtraction):
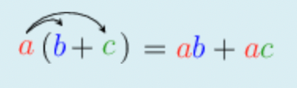
- The process of writing product expressions as sum expressions is called expansion. It is sometimes also referred to as multiplication of algebraic expressions.
