10.6 Constructing triangles
In this section, you will learn how to construct different triangles using given information. A triangle has three sides and three interior angles. However, we do not need to know the lengths of all three sides and the sizes of all three angles in order to construct a triangle.
To construct a triangle, we only need to know three properties of the triangle. Any of these three combinations provides enough information to construct a triangle:
- the lengths of all three sides (side, side, side)
- the sizes of two interior angles and the length of the side between them (angle, side, angle)
- the lengths of two sides and the size of the angle between them (side, angle, side).
It is helpful to remember the following important properties of triangles:
- The longest side of a triangle lies opposite the biggest angle of the triangle. (It is impossible to construct a triangle where the longest side is not opposite the biggest angle.)
- The shortest side of a triangle lies opposite the smallest angle of the triangle.
- The sum of the lengths of the two shorter sides of the triangle must be greater than the length of the longest side of the triangle.

Constructing a triangle given two sides and an included angle
In this section, you will construct triangles for which you are given two sides as well as the included angle.
- included angle
- the angle between two sides of a triangle
The diagram below illustrates an included angle.
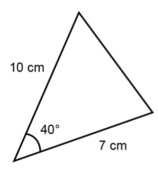
Before starting a construction, it is a good idea to draw a rough sketch of the triangle. Label the sketch correctly and write down all the given information.
Worked Example 10.11: Constructing a triangle given two sides and the included angle
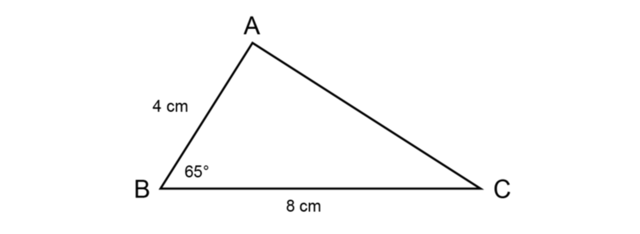
Construct \(\triangle ABC\) with \(AB = 4 \text{ cm}\), \(A\hat{B}C = 65^{\circ}\) and \(BC = 8 \text{ cm}\). You may use a protractor for this construction.
Draw a rough sketch of the triangle.
Read the given information carefully and fill everything in on the rough sketch. Label the vertices of the triangle.
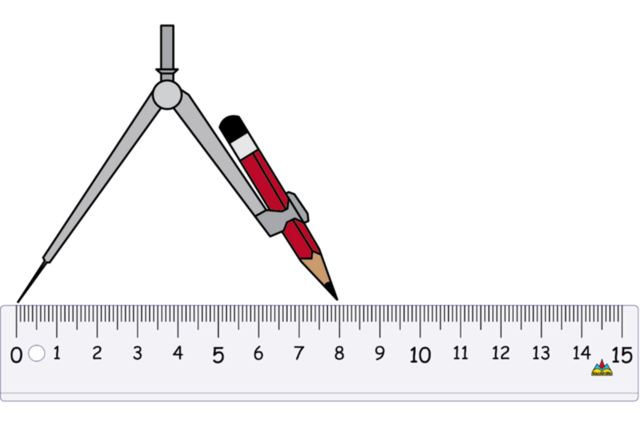
Draw a line segment \(BC\).
Draw a line segment (longer than \(8 \text{ cm}\)) and mark point \(B\). Use the compass to measure a length of \(8 \text{ cm}\) on your ruler.
Keep the compass width the same and place the compass on point \(B\). Then draw a small arc to mark off a length of \(8\text{ cm}\). Label the point \(C\).

Use a protractor to measure and draw the included angle.
Put the origin of the protractor on point \(B\). Use the inner scale of the protractor to find \(65^{\circ}\). Make a small dot at the edge of the protractor. Then draw a line through the dot and point \(B\).
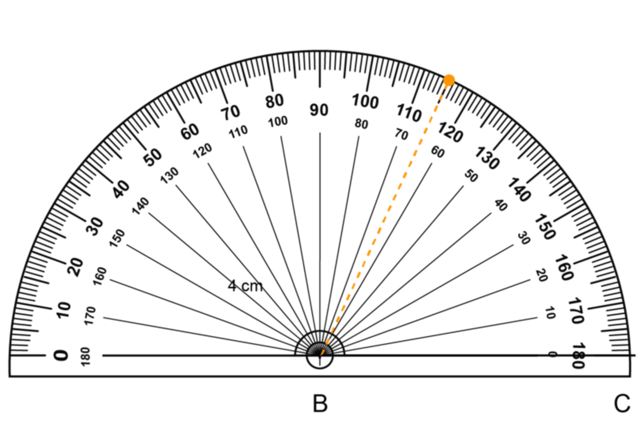
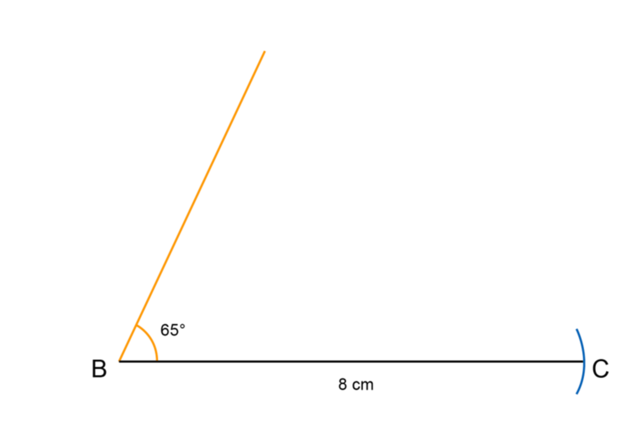
Measure the length of the second side of the triangle.
Use the compass to measure a length of \(4 \text{ cm}\) on your ruler. Keeping the compass width the same, place the compass on point \(B\) and draw a small arc to mark off a length of \(4 \text{ cm}\). Label the point \(A\).
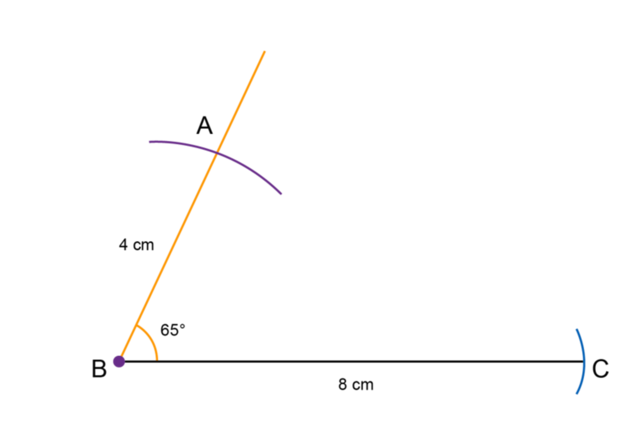
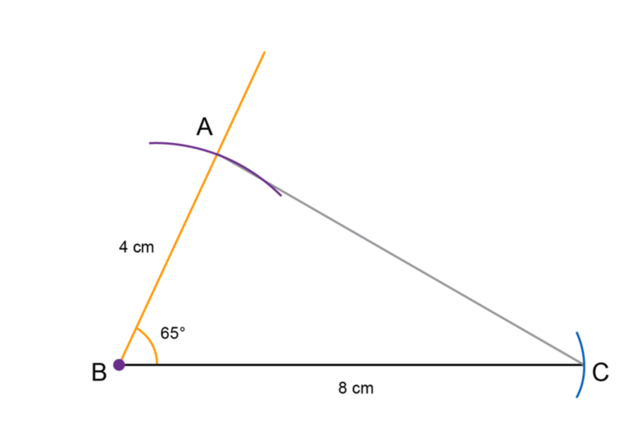
Draw the third side of the triangle.
Use a ruler to join points \(A\) and \(C\).
This completes the construction of \(\triangle ABC\).
- Never erase the construction lines after you have completed a construction. These may be important for giving marks for your work.
- The constructions provided here may not display at the exact size on all devices. Check your own constructions to make sure they are correct.
Construct triangles given two sides and the included angle
Construct \(\triangle DEF\) with \(DE = 6 \text{ cm}\), \(\hat{E} = 50^{\circ}\) and \(EF = 7 \text{ cm}\).
Construct \(\triangle PQR\) with \(PQ = 7 \text{ cm}\), \(\hat{Q} = 120^{\circ}\) and \(QR = 5 \text{ cm}\).
Construct \(\triangle XYZ\) with \(XY = 2 \text{ cm}\), \(\hat{Q} = 90^{\circ}\) and \(YZ = 8 \text{ cm}\).
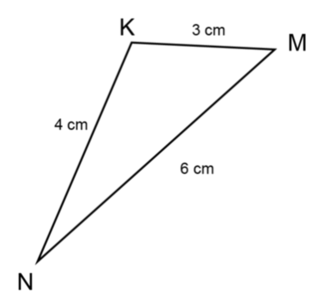
Make an accurate construction of \(\triangle KLM\).

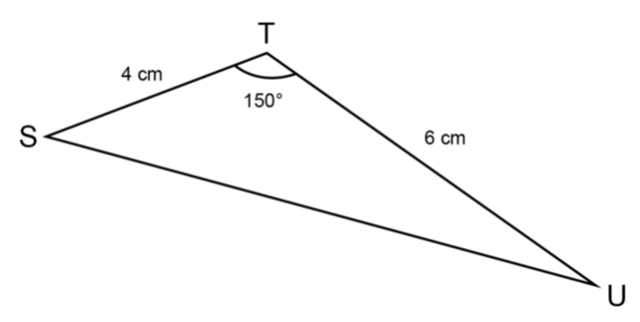
Make an accurate construction of \(\triangle STU\).
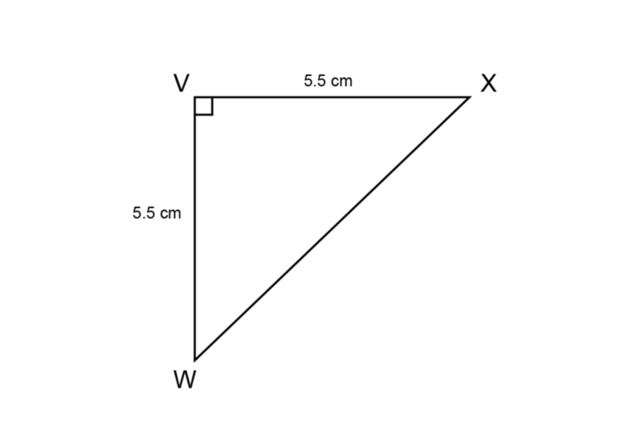
Make an accurate construction of \(\triangle VWX\).
Construct a triangle given two angles and the side between them
In this section, you will construct triangles for which you are given two angles and the length of the side between the two angles.
Worked Example 10.12: Constructing a triangle given two angles and the side between them
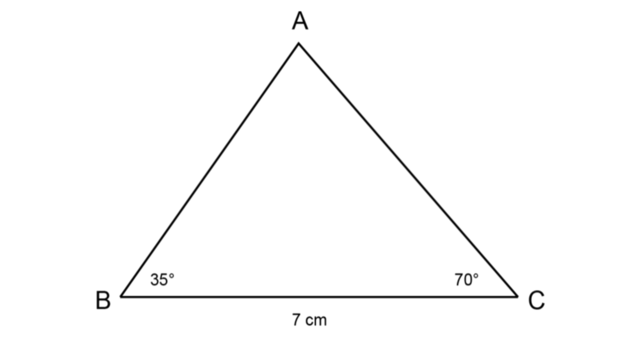
Construct \(\triangle ABC\) with \(\hat{B} = 35^{\circ}\), \(\hat{C} = 70^{\circ}\) and \(BC = 7 \text{ cm}\). You may use a protractor for this construction.
Draw a rough sketch of the triangle.
Read the given information carefully and fill everything in on the rough sketch. Label the vertices of the triangle.
Construct the line segment \(BC\).
Draw a line segment (longer than \(7 \text{ cm}\)) and mark point \(B\). Use the compass to measure a length of \(7 \text{ cm}\) on your ruler.
Keeping the compass width the same, place the compass on point \(B\) and make an arc on the line. Label point \(C\).
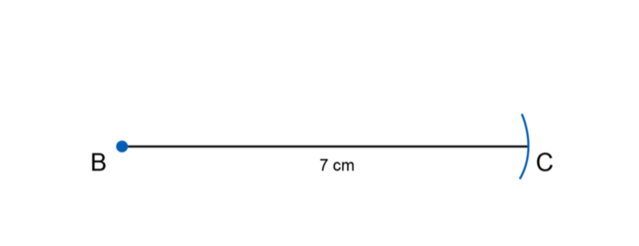
Use a protractor to measure and draw \(\hat{B}\).
Put the origin of the protractor on point \(B\). Use the inner scale of the protractor to find \(35^{\circ}\). Make a small dot at the edge of the protractor and then draw a line through the dot and point \(B\).
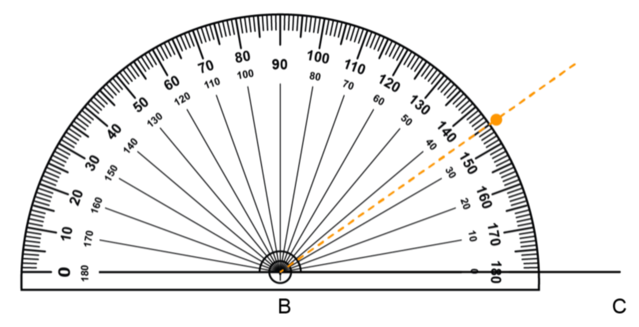

Use a protractor to measure and draw \(\hat{C}\).
Put the origin of the protractor on point \(C\). On the protractor, use the outer scale from the left and find \(70^{\circ}\). Make a small dot at the edge of the protractor.
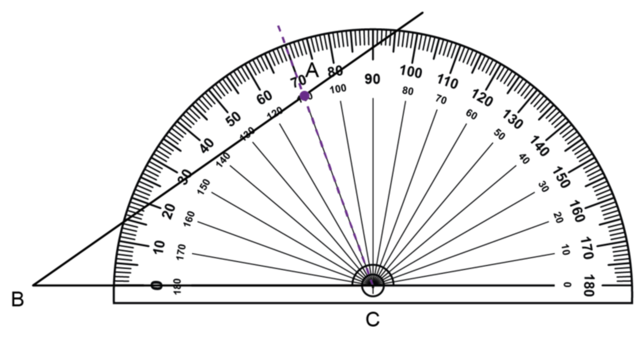
Draw the line segment \(CA\).
Use a ruler to draw a line through the dot and point \(C\). Label the point where the two lines intersect, point \(A\).
This completes the construction of \(\triangle ABC\).
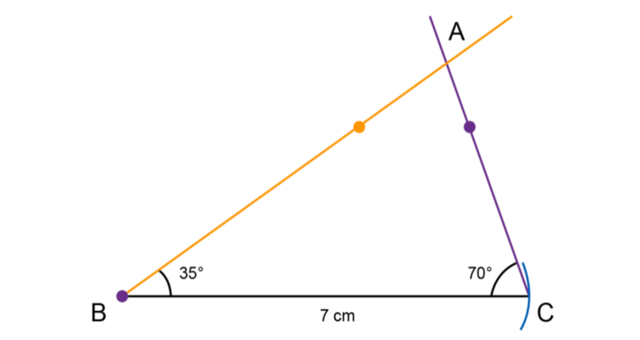
Construct a triangle given two angles and the side between them
Construct \(\triangle DEF\) with \(\hat{E} = 50^{\circ}\), \(EF = 8 \text{ cm}\) and \(\hat{F} = 60^{\circ}\). You may use a protractor.
Construct \(\triangle PQR\) with \(\hat{R} = 130^{\circ}\), \(\hat{Q} = 30^{\circ}\) and \(RQ = 4 \text{ cm}\). You may use a protractor.
Use a compass and a ruler to construct \(\triangle XYZ\) with \(YZ = 6 \text{ cm}\), \(\hat{Y} = 60^{\circ}\) and \(\hat{Z}\), a right angle.
Make an accurate construction of \(\triangle DTM\) as shown below. You may use a protractor. (Note that the diagram is not to scale.)

Make an accurate construction of \(\triangle JME\) as shown below. You may use a protractor. (The given diagram is not to scale.)
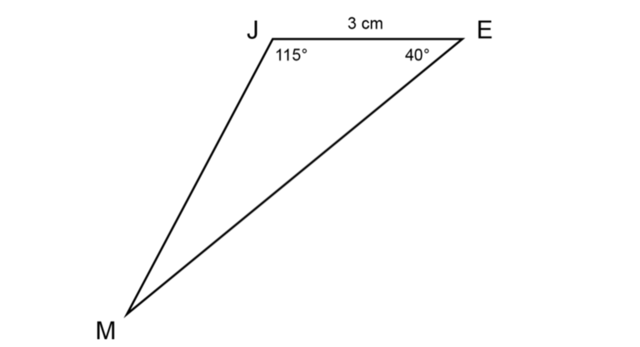
Use a compass and a ruler to construct \(\triangle CDE\) as shown below. (The given diagram is not to scale.)

Why is it impossible to construct \(\triangle KLM\) if \(\hat{L} = 95^{\circ}\), \(LM = \text{7,5} \text{ cm}\) and \(\hat{M} = 110^{\circ}\)?
Construct a triangle given all three sides
Worked Example 10.13: Constructing a triangle given all three sides
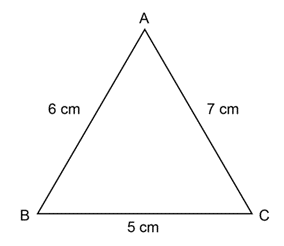
Construct \(\triangle ABC\) with \(AB = 6 \text{ cm}\), \(BC = 5 \text{ cm}\) and \(CA = 7 \text{ cm}\).
Draw a rough sketch of the triangle.
Read the given information carefully and draw a rough sketch. Label the vertices of the triangle and the lengths of the sides.
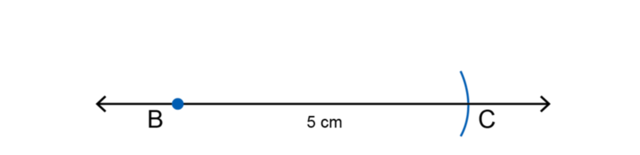
Draw a line segment \(BC\).
Draw a line segment (longer than \(5 \text{ cm}\)) and mark point \(B\). Use a compass to measure a length of \(5 \text{ cm}\) on your ruler. Keeping the compass width the same, place the compass on point \(B\) and draw a small arc to mark off a length of \(5 \text{ cm}\). Label the point \(C\).
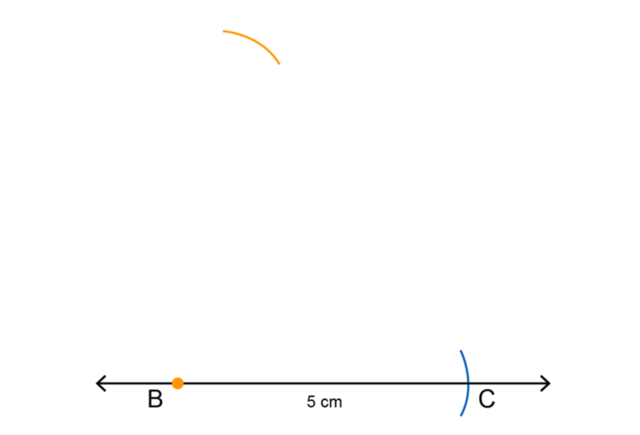
Draw an arc to mark the length of side \(AB\).
Use the compass to measure a length of \(6 \text{ cm}\) on your ruler. Keeping the compass width the same, place the compass on point \(B\) and draw an arc above line \(BC\) and between \(B\) and \(C\).
Construct an arc to mark the length of side \(CA\).
Use your compass to measure a length of \(7 \text{ cm}\) on your ruler. Keeping the width of the compass the same, place the compass on point \(C\) and make a third arc that intersects the second arc. Label the point of intersection \(A\).

Draw \(AB\) and \(CA\) to complete \(\triangle ABC\).
Use a ruler to draw \(AB\) and \(CA\).
Construct a triangle given all three sides
Construct these triangles. Note that diagrams are not to scale.
- \(\triangle ABC\) with sides \(AB = 6 \text{ cm}\), \(BC = 7 \text{ cm}\) and \(CA = 4 \text{ cm}\).
- \(\triangle KLM\) with sides \(KL = 10 \text{ cm}\), \(LM = 5 \text{ cm}\) and \(MK = 8 \text{ cm}\).
- \(\triangle PQR\) with sides \(PQ = 5 \text{ cm}\), \(QR = 9 \text{ cm}\) and \(RP = 11 \text{ cm}\).
Use a ruler and a compass to construct \(\triangle PQR\).

Use a ruler and a compass to construct \(\triangle KMN\).