13.6 Chapter summary

• Instead of writing \(2\) fifths, we may write \(\frac{2}{5}\). This is called the common fraction notation. The number \(5\) below the line is called the denominator. The number \(2\) above the line is called the numerator.
• \(\frac{3}{4}\), \(\frac{6}{8}\), \(\frac{15}{20}\), \(\frac{45}{60}\) are all different ways of expressing the same number. They are therefore called equivalent fractions.
• Proper fractions are fractions that are less than one; the numerator is always less than the denominator.
• Improper fractions are fractions that are greater than or equal to one; the numerator is larger than or equal to the denominator.
• Mixed numbers (mixed fractions) are numbers that have an integer part and a fraction part; the fraction part must be a proper fraction (less than one).
• When you simplify a fraction, you must reduce the numbers in the fraction to the smallest possible values. We do this by cancelling the highest common factor from the numerator and the denominator.
• To convert a mixed number to an improper fraction, start at the denominator; then follow the solid arrow around and multiply by the integer in the front; then continue following the dashed arrow and add the numerator. Keep the same denominator:

\[\begin{align} 4\frac{2}{3} = \frac{(3 \times 4) + 2}{3} = \frac{12 + 2}{3} = \frac{14}{3} \end{align}\]

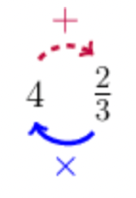
• To convert an improper fraction to a mixed number, divide the numerator by the denominator (change the fraction to a division problem).

\[\begin{align} \frac{5}{2} = 5 \div 2 \end{align}\]

Start by finding out how many times \(2\) fits into \(5\). \(2 \times 2 = 4\), which leaves \(1\) as a remainder. Keep the denominator the same.

\[\begin{align} \frac{5}{2} = 2\frac{1}{2} \end{align}\]

• To add (or subtract) fractions:
  • Make sure that they have the same denominators. Convert the fractions to equivalent fractions that have the same denominators using the lowest common denominator (LCD), if necessary.
  • Add (or subtract) the numerators.
• To multiply fractions:
  • Cross cancel any common factors. (This is not strictly necessary, but it will make your life easier.)
  • Multiply the numerators, and multiply the denominators.
• Multiplying fractions follows this rule:

\[\begin{align} \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d} \end{align}\]

• To divide fractions:
  • “Tip and times”: multiply by the reciprocal of the fraction in the divisor (the second fraction).
  • Multiply the fractions as normal.
• Dividing fractions follows this rule, which uses the reciprocal of the second fraction:

\[\begin{align} \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c} \end{align}\]

• Remember that per cent means per hundred. For example, \(\frac{2}{10} = \frac{20}{100}\) which is \(20\) per hundred \(= 20\%\). To convert a fraction to a percentage, find the equivalent fraction with the denominator \(100\). The numerator of the new fraction shows you the amount per hundred, or per cent.
• To calculate the percentage increase or decrease: