Chapter 12: Geometry of straight lines

12.1 Introduction

In this chapter, we will explore the relationships between pairs of angles that are created when:

• straight lines intersect (meet or cross)
• lines are perpendicular to each other
• a third line crosses two parallel lines

You will come to understand what is meant by vertically opposite angles, corresponding angles, alternate angles and co-interior angles. You will then use your knowledge to help you work out unknown angles in geometric figures.

Notation

An angle is formed when two straight lines meet at a point. The point where the lines meet is called the vertex. Angles are labelled with a caret or 'hat' on a letter, for example, $\hat{A}$.

angle

the space between two straight lines that meet at a point

vertex

the point at which two straight lines meet

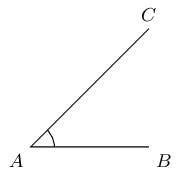
In this diagram, angle $\hat{A}$ is formed between line segments $BA$ and $CA$. We can also name the angle according to the line segments that make up the angle, for example $C\hat{A}B$ or $B\hat{A}C$.

The $\angle$ symbol is a short method of writing the word angle in geometry, and is often used in phrases such as "the sum of $\angle$s in $\triangle$".