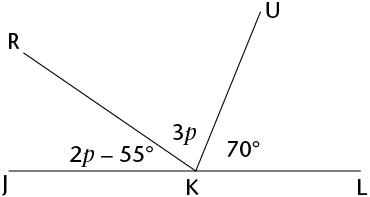
Calculate the size of:
- \(p\)
- \(R\hat{K}U\)
- \[\begin{align} 2p-55°+3p+70° &=180° &(\angle\text{s on a straight line}) \\ 5p+125°&=180° \\ 5p&=55° \\ p&=11° \end{align}\]
- \[R\hat{K}U = 3p =3(11^{\circ})=33^{\circ}\]
|
Previous
Chapter summary
|
Next
Introduction
|

Calculate the size of:
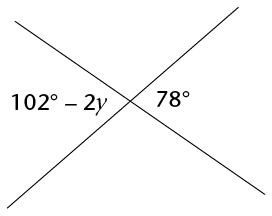
Calculate the size of \( y \)
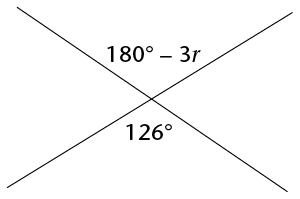
Calculate the size of \( r \)
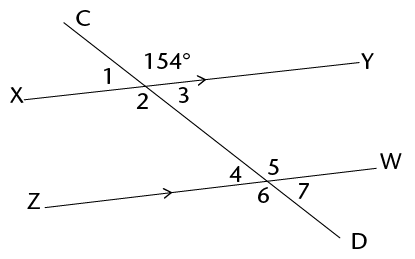
Find the sizes of all the angles \(\hat{1}\) to \(\hat{7}\).
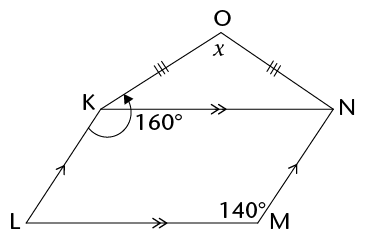
In the diagram, \(OK = ON\), \(KN \parallel LM\), \(KL \parallel MN\) and \(\hat{LKO}=160^{\circ}\). Calculate the value of \(x\). Give reasons for your answers.
|
Previous
Chapter summary
|
Table of Contents |
Next
Introduction
|