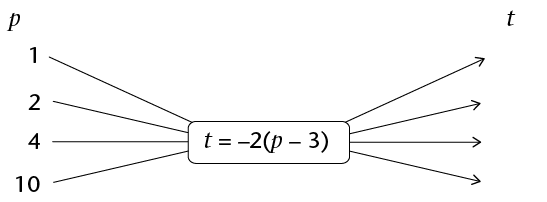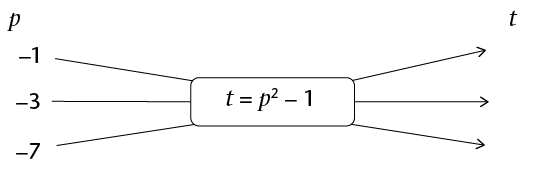An algebraic expression is a description of certain calculations that have to be done in a certain order. In this chapter, you will be introduced to the language of algebra. You will also learn about expressions that appear to be different but that produce the same results when evaluated. When we evaluate an expression, we choose or are given a value of the variable in the expression. Because now we have an actual value, we can carry out the operations (\(+, -, \times, \div)\) in the expression using this value.
Algebraic language
Words, diagrams and symbols
- Complete this table
Words
Flow diagram
Expression
Multiply a number by two and add six to the answer.

\( 2 \times x + 6\)
(a)
Add three to a number and then multiply the answer by two.
(b)

(c)
\( 7 + 4 \times x\)
(d)
\( 10 - 5 \times x\)
An algebraic expression indicates a sequence of calculations that can also be described in words or with a flow diagram.
The flow diagram illustarte the order in which the calculations must be done
In algebraic language the multipliaction sign is usually ommited. So we write \(2x\) instead of \( 2 \times x\)
We also write \( x \times 2 \text{ as } 2x \)
- Write the following
expressions in 'normal' algebraic
language:
- \( 2 \times a + b\)
- \(a2\)
- \( 2 \times a + b\)
Looking different but yet the same
- Complete the table by
calculating the numerical values of the expressions for the
values of \(x\). Some answers for \(x\) = 1 have been
done for you as an example.
\(x\)
1
3
7
10
(a)
\(2x + 3x\)
\(2 \times 1 + 3 \times 1\)
\(2 + 3 = 5\)
(b)
\(5x\)
(c)
\(2x + 3\)
(d)
\(5x^2\)
\(5 \times (1)^2\)
\(5 \times 1 = 5\)
- Do the expressions
\(2x + 3\) and \(5x\), in question 1 above, produce
different answers or the same answer for:
- \(x = 3\)?
- \(x = 10\)?
- \(x = 3\)?
- Do the expressions \(2x + 3\) and \(5x\) produce different answers or the same answer
for:
- \(x = 3\)?
- \(x = 10\)?
- \(x = 3\)?
- Write down all the
algebraic expressions in question 1 that have the same
numerical value for the same value(s) of
\(x\), although they may look different. Justify your
answer.
One of the things we do in algebra is to evaluate expressions. When we evaluate an expression we choose or are given a value of the variable in the expression. Because now we have an actual value we can carry out the operations in the expression using this value, as in the examples given in the table.
Algeraic expressions that have the same numarical value for the same value of x but look different are called equivalent expressions.
- Say whether the
following statements are true or false. Explain your answer in
each case.
- The expressions \(2x + 3x\)
and \(5x\) are equivalent.
- The expressions \(2x + 3\)
and \(5x\) are
equivalent.
- The expressions \(2x + 3x\)
and \(5x\) are equivalent.
- Consider the expressions \(3x + 2z + y\) and \(6xyz\).
Remember that \(6xyz\) is the same as \(6 \times x \times y \times z\).
- What is the value of \(3x + 2z + y\) for \( x = 4\) , \(y = 7\) and
\(z = 10\)?
- What is the value of \(6xyz\)
for \( x = 4\) , \(y = 7\) and \(z = 10\)?
- Are the expressions \(3x + 2z + y\) and \(6xyz\) equivalent? Explain.
- What is the value of \(3x + 2z + y\) for \( x = 4\) , \(y = 7\) and
\(z = 10\)?
To show that the two expressions in question 5(a) are equivalent we write \(2x + 3x = 5x\).
We can explain why this is so:
\(2x + 3x = (x + x) + (x + x + x) = 5x\)
We say the expression \(2x + 3x\) simplifies to \(5x\).
The term \(3x\) is a product. The number 3 is called the coefficient of \(x\).
- In each case below, write down
an expression equivalent to the one given.
- \(3x + 3x\)
- \(3x + 8x + 2x\)
- \(8b + 2b + 2b\)
- \(7m + 2m + 10m\)
- \(3x^2 + 3x^2\)
- \(3x^2 + 8x^2 + 2x^2\)
- \(3x + 3x\)
- What is the coefficient of
\(x^2\) for the
expression equivalent to \(3x^2 + 8x^2 + 2x^2\)?
In an expression that can be written as a sum, the different parts of the expression are called the terms of the expression. For example, \(3x,2z \text{ and } y\) are the terms of the expression \(3x + 2z + y\).
An expression can have like terms or unlike terms or both.
Like terms are terms that have the same variable(s) raised to the same power. The terms \(2x\) and \(3x\) are examples of like terms.
-
- Calculate the numerical value of
\(10x + 2y\) for \(x = 3\) and \( y = 2\) by
completing the empty spaces in the diagram.
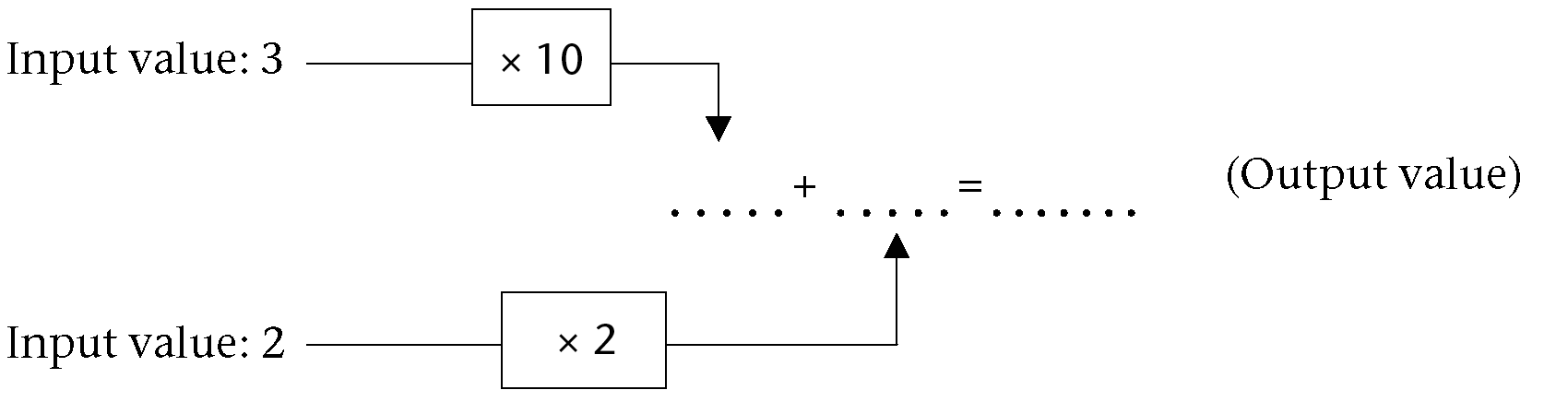
- What is the output value for the
expression \(12xy\) for \(x = 3 \text{ and } y = 2\)?
- Are the expressions \(10x +2y\) and \(12xy\) equivalent? Explain.
- Are the terms \(10x\) and \(2y\)
like or unlike terms? Explain.
- Calculate the numerical value of
\(10x + 2y\) for \(x = 3\) and \( y = 2\) by
completing the empty spaces in the diagram.
-
- Which of the following algebraic
expressions do you think will give the same results?
A. \( 6x + 4x\)
B. \(10x\)
C. \(10x^2\)
D. \(9x + x\)
- Test the algebraic expressions you have
identified for the following values of \(x\)
\( x = 10\)
\( x = 17\)
\( x = 54\)
- Are the terms \(6x\) and \(4x\) like or unlike terms? Explain.
- Are the terms \(10x\) and \(10x^2\) like or
unlike terms? Explain.
- Which of the following algebraic
expressions do you think will give the same results?
- Ashraf and Hendrik
have a disagreement about whether the terms \(7x^2y^3\) and \(301y^3x^2\) are like terms or not.
Hendrik thinks they are not, because in the first term the \(x^2\) comes
before the \(y^3\) whereas in the second term \(y^3\) comes
before the \(x^2\).
Explain to Hendrik why his argument is not correct.
- Explain why the terms \(5abc, 10acb \text{
and } 15cba\) are like terms.
Add and subtract like terms
Rearrange terms and then combine like terms
- Complete the table by
evaluating the expressions for the given values of
\(x\).
\(x\)
1
2
10
\(30x + 80\)
\(30 \times 1 + 80\)
\(= 30 + 80 = 110\)
\(5x + 20\)
\(30x + 80 + 5x + 20\)
\(35x + 100\)
\(135x\)
- Write down all the expressions
in the table that are equivalent.
- Tim thinks that the
expressions \(135x\) and \(35x +100\) are equivalent
because for \(x = 1\) they both have the same numerical
value 135.
Explain to Tim why the two expressions are not equivalent.
We have already come across the commutative and associative properties of operations. We will now use these properties to help us form equivalent algebraic expressions.
Commutative property
The order in which we add or multiply numbers does not change the answer: \(a + b = b + a\) and \( ab = ba\)
Associative property
The way in which we group three or more numbers when adding or multiplying does not change the answer: \((a +b)+c = a + (b + c)\) and \((ab)c = a(bc)\)
We can find an equivalent expression by rearranging and combining like terms, as shown below:
\(30x + 80 + 5x + 20\)
Hence \(30x + (80 + 5x) + 20\)
Hence \(30x + (80 + 5x) + 20\)
\(= (30x + 5x) + (80 + 20)\)
\(= 35x + 100\)
The terms 80 and 20 are called constants. The numbers 30 and 5 are called coefficients.
Brackets are used in the expression above to show how the like terms have been rearranged.
Like terms are combined to form a single term.
The terms \(30x\) and \(5x\) are combined to get the new term \(35\) and the terms 80 and 20 are combined to form the new term 100. We say that the expression \(30x + 80 + 5x + 20\) is simplified to a new expression \(35x + 100\).
- Simplify the following
expressions:
- \(13x + 7 + 6x - 2\)
- \(21x - 8 + 7x + 15\)
- \(8c - 12d + 5c - 7c\)
- \(3abc + 4 + 7abc - 6\)
- \(12x^2 + 2x - 2x^2 + 8x\)
- \(7m^3 + 7m^2 + 9m^3 + 1\)
- \(13x + 7 + 6x - 2\)
When you are not sure about whether you correctly simplified an expression, it is always advisable to check your work by evaluating the original expression and the simplified expression for some values. This is a very useful habit to have.
When we use a value of the variable in the expression we call that substitution.
- Make a simpler expression that is equivalent to the given
expression. Test your answer for three different values of
x, and redo your work until you get it right.
- \((15x + 7y) + (25x + 3 + 2y)\)
- \(12mn + 8mn\)
- \((15x + 7y) + (25x + 3 + 2y)\)
In questions 6 to 8 below, write down the letter representing the correct answer. Also explain why you think your answer is correct.
- The sum of \( 5x^2 + x + 7\) and \(x - 9\) is:
A. \(x^2 -2\)
B. \(5x^2 + 2x +16\)
C. \(5x^2 + 16\)
D. \(5x^2 + 2x - 2\)
- The sum of \(6x^2 - x + 4\) and \(x^2 - 5\)
is equivalent to:
A. \(7x^2 - x + 9\)
B. \(7x^2 - x - 1\)
C. \(6x^4 - x - 9\)
D. \(7x^4 - x - 1\)
- The sum of \(5x^2 + 2x + 4\) and \(3x^2 - 5x - 1\) can be
expressed as:
A. \( 8x^2 + 3x + 3\)
B. \(8x^2 + 3x - 3\)
C. \(8x^2 - 3x + 3\)
D. \(8x2 - 3x - 3\)
Combining like terms is a useful algebraic habit. It allows us to replace an expression with another expression that may be convenient to work with.
Do the following questions to get a sense of what we are talking about.
Convenient replacements
- Consider the
expression \( x + x + x + x + x + x + x + x + x + x\). What is
the value of the expression in each of the following cases?
- \(x = 2\)
- \(x = 50\)
- \(x = 2\)
- Consider the \(x + x + x + z + z + y\). What is the value of the expression in each of the
following cases?
- \(x = 4, y = 7, z = 10\)
- \(x = 0, y = 8, z = 22\)
- \(x = 4, y = 7, z = 10\)
- Suppose you have to
evaluate \(3x + 7x\) for \(x = 20\). Will
calculating \(10 \times 20\) give the correct answer? Explain.
Suppose we evaluate the expression \(3x + 7x\) for \(x = 20\) without first combining the like terms. We will have to do three calculations, namely \(3 \times 20\), then \(7 \times 20\) and then find the sum of the two: \(3 \times 20 + 7 \times 20 = 60 + 140 = 200\).
But if we first combine the like terms \(3x \text{ and } 7x\) into one term \(10x\), we only have to do one calculation: \(10 \times 20 = 200\). This is one way of thinking about the convenience or usefulness of simplifying an algebraic expression.
- The expression \(5x + 3x\) is given and you are required to evaluate
it for \(x = 8\). Will calculating \(8 \times 8\) give the
correct answer? Explain.
- Suppose you have to
evaluate \(7x + 5\) for \(x = 10\). Will calculating \(12
\times 10\) give the correct answer? Explain.
- The expression
\(5x + 3\) is given and you have to evaluate it for \(x
= 8\). Will calculating \(8 \times 8\) give the correct answer?
Explain.
Samantha was asked to evaluate the expression \(12x^2 + 2x - 2x^2 + 8x\) for \(x = 12\). She thought to herself that just substituting the value of x directly into the terms would require a lot of work. She first combined the like terms as shown below:
\(12x^2 {\bf- 2x^2 + 2x} +8x \\ 10x^2 + 10x\)
The terms \(+2x\) and \(-2x^2\) change positions by the commutative property of operations.
Then for \(x =10\), Samantha found the value of \(10x^2 + 10x\) by calculating
\(10 \times 10^2 + 10 \times 10 \\ = 1000 + 100 \\ = 1100\)
Use Samatha's way of thinking for questions 7 to 9.
- What is the value of \(12x + 25x + 75x + 8x\) when \(x =6\)
- Evaluate \( 3x^2 + 7 + 2x^2 + 3\) for \(x = 5\).
- When Zama was asked to
evaluate the expression \(2n - 1 + 6n \) for \(n
= 4\), she wrote down the following:
\(\begin{align} 2n - 1 + 6n &= n + 6n = 6n^2 \\ \text{Hence for } n &= 4: 6 \times (4)^2 = 6 \times 8 = 48 \end{align}\)
Explain where Zama went wrong and why.
- Complete the table.
Words
Flow diagram
Expression
(a)
Multiply a number by three and add two to the answer.

(b)
\(9x-6\)
(c)

\(7x-3\)
- Which of the following pairs
consist of like terms? Explain.
A.\(3y; -7y\)
B. \(14e^2; 5e\)
C \(3y^2z; 17y^2z\)
D. \(-bcd; 5bd\)
- Write the following in the
'normal' algebraic way:
- \(c2 + d3\)
- \( 7 \times d \times e \times f \)
- \(c2 + d3\)
- Consider the expression \(12x^2 - 5x + 3\).
-
What is the number 12 called?
-
Write down the coefficient of \(x\).
- What name is given to
the number 3?
-
What is the number 12 called?
- Explain why the terms \(5pqr\) and \(-10prq\) and \(15qrp\) are like
terms.
- If \(y =7\), what is the value of
each of the following?
- \(y+8\)
- \(9y\)
- \(7 -y\)
- \(y+8\)
- Simplify the
following expressions:
- \(18c + 12d + 5c - 7c\)
- \(3def + 4 + 7def - 6\)
- \(18c + 12d + 5c - 7c\)
- Evaluate the
following expressions for \(y = 3; z =-1\):
- \(2y^2 + 3z\)
- (\(2y)^2 + 3z\)
- \(2y^2 + 3z\)
- Write each
algebraic expression in the simplest form.
- \(5y + 15y\)
- \(5c + 6c - 3c + 2c\)
- \(4b + 3 + 16b - 5\)
- \(7m + 3n + 2 - 6m\)
- \(5h^2 + 17 - 2h^2 + 3\)
- \(7e^2f + 3ef + 2 + 4ef\)
- \(5y + 15y\)
- Evaluate
the following expressions:
- \(3y+ 3y + 3y + 3y + 3y + 3y \) for \(y = 18\)
- \(13y + 14 - 3y + 6\) for \(y = 200\)
- \(20 - y^2 + 101y^2 + 80\) for \(y = 1\)
- \(12y^2 + 3yz + 18y^2 + 2yz\) for (\9y=3\) and \( z = 2\)
- \(3y+ 3y + 3y + 3y + 3y + 3y \) for \(y = 18\)
Algebraic equations
In this chapter you will learn to find numbers that make certain statements true. A statement about an unknown number is called an equation. When we work to find out which number will make the equation true, we say we solve the equation. The number that makes the equation true is called the solution of the equation.
Setting up equations
An equation is a mathematical sentence that is true for some numbers but false for other numbers. The following are examples of equations:
\[x + 3 = 11 \text{ and } 2^x = 8\]
\(x + 3 = 11\) is true if \(x =8\), but false if \(x =3\).
When we look for a number or numbers that make an equation true we say that we are solving the equation. For example , \(x = 4\) is the solution of \(2x + 8\) because it makes \(2x +8\)true. (Check: \(2 \times 4 = 8\)
Looking for numbers to make statements true
- Are the following statements
true or false? Justify your answer.
- \(x - 3 = 0\), if \(x = -3\)
- \(x^3 = 8\), if \(x = -2\)
- \(3x = -6\), if \(x = -3\)
- \(3x = 1\), if \(x = 1\)
- \(6x + 5 = 47\), if \(x = 7\)
- \(x - 3 = 0\), if \(x = -3\)
- Find the original number. Show
your reasoning.
- A number multiplied by 10 is 80.
- Add 83 to a number and the answer is 100.
- Divide a number by 5 and the answer is 4.
- Multiply a number by 4 and the answer is 20.
- Twice a number is 100.
- A number raised to the power 5 is 32.
- A number raised to the power 4 is -81.
- Fifteen times a number is 90.
- 93 added to a number is -3.
- Half a number is 15.
- A number multiplied by 10 is 80.
- Write the equations
below in words using "a number" in place of the letter symbol
\(x\). Then write what
you think "the number" is in each case.
Example: \(4 +x = 23\). Four plus a number equals twenty-three. The number is 19.
- \(8x = 72\)
-
\( \frac{2x}{5} = 2 \)
-
\( 2x+ 5 = 21\)
-
\( 12 + 9x = 30\)
-
\(30 - 2x = 40\)
-
\(5x + 4 = 3x+ 10\)
- \(8x = 72\)
Solving equations by inspection
The answer is in plain sight
-
Seven equations are given below the table. Use the table to
find out for which of the given values of \(x\) it will be
true that the left-hand side of the equation is equal to the
right-hand side.
You can read the solutions of an equation from a table.
\(x\)
-3
-2
-1
0
1
2
3
4
\(2x + 3\)
-3
-1
1
3
5
7
9
11
\(x + 4\)
1
2
3
4
5
6
7
8
\(9 -x\)
12
11
10
9
8
7
6
5
\(3x -2\)
-11
-8
-5
-2
1
4
7
10
\(10x -7\)
-37
-27
-17
-7
3
13
23
33
\(5x +3\)
-12
-7
-2
3
8
13
18
23
\(10 - 3x\)
19
16
13
10
7
4
1
-2
- \(2x + 3 = 5x + 3\)
- \(5x + 3 = 9 - x\)
- \(2x + 3 = x+4\)
- \(10x -7 = 5x + 3\)
- \(3x -2 = x+4\)
- \(9 -x = 2x + 3\)
- \(10 -3x = 3x - 2\)
- \(2x + 3 = 5x + 3\)
Two or more equations can have the same solution. For example, \(5x = 10\) and \(x + 2 = 4\) have the same solution; \(x = 2\) is the solution for both equations.
Two equations are called equivalent if they have the same solution.
- Which of the equations in
question 1 have the same solutions? Explain.
- Complete the table below. Then
answer the questions that follow.
You can also do a search by narrowing down the possible solution to an equation.
\(x\)
0
5
10
15
20
25
30
35
40
\(2x + 3\)
\(3x -10\)
- Can you find a solution
for \(2x + 3 = 3x - 10\) in the table?
- What happens to the values
of \(2x + 3\) and \(3x - 10\) as \(x\) increases? Do
they become bigger or smaller?
- Is there a point where the value of
\(3x - 10\) becomes bigger or smaller than the value of
\(2x + 3\) as the value of \(x\) increases? If so,
between which \(x\)-values does this happen?
This point where the two expressions are equal is called the break-even point.
- Now that you narrowed down where the
possible solution can be, try other possible values for
\(x\) until you find
out for what value of \(x\) the statement \(2x + 3 = 3x - 10\) is true.
"Searching" for the solution of an equation by using tables or by narrowing down to the possible solution is called solution by inspection.
- Can you find a solution
for \(2x + 3 = 3x - 10\) in the table?
More examples
Looking for and checking solutions
- What is the solution for the
equations below?
- \(x - 3 = 4\)
- \(x + 2 = 9\)
- \(3x = 21\)
- \(3x + 1 = 22\)
- \(x - 3 = 4\)
When a certain number is the solution of an equation we say that the number satisfies the equation. For example, \(x=4\) satisfies the equation \(3x=12\) because \(3 \times 4 = 12\).
- Choose the number in brackets that
satisfies the equation. Explain your choice.
- \(12x = 84\) {5; 7; 10; 12}
-
\( \frac{84}{x} = 12\) {-7; 0; 7; 10}
-
\(48 = 8k + 8\) {-5; 0; 5; 10}
-
\(19 - 8m = 3\) {-2; -1; 0; 1; 2}
-
\(20 = 6y - 4\) {3; 4; 5; 6}
-
\(x^3 = -64\) {-8; -4; 4; 8}
-
\(5^x =125\) {-3; -1; 1; 3}
-
\(2^x = 8\) {1; 2; 3; 4}
-
\(x^2 = 9\) {1; 2; 3; 4}
- \(12x = 84\) {5; 7; 10; 12}
- What makes the following
equations true? Check your answers.
- \(m + 8 = 100\)
- \( 80 = x + 60 \)
- \(26 - k = 0 \)
- \(105 \times y = 0\)
- \( k \times 10 = 10 \)
- \(5x = 100\)
- \( \frac{15}{t} = 5 \)
- \( 3 = \frac{t}{5} \)
- \(m + 8 = 100\)
- Solve the equations below by
inspection. Check your answers.
- \( 12x + 14 = 50 \)
- \(100 = 15m + 25\)
- \( \frac{100}{x} =20\)
- \( 7m + 5 = 40\)
- \(2x + 8 = 10\)
- \(3x + 10 = 31\)
- \(-1 + 2x = -11\)
- \(2 + \frac{x}{7} = 5\)
- \(100 = 64 + 9x\)
- \( \frac{2x}{6}= 4\)
- \( 12x + 14 = 50 \)
Term revision and assessment
Revision
Show all your steps of working.
Whole numbers
-
- Write both 300 and 160 as products of
prime factors.
- Determine the HCF and LCM of 300 and
160.
- Write both 300 and 160 as products of
prime factors.
- Tommy, Thami and Timmy
are given birthday money by their grandmother in the ratio of
their ages. They are turning 11, 13 and 16 years old,
respectively. If the total amount of money given to all three
boys is R1 000, how much money does Thami get on his
birthday?
- Tshepo and his family
are driving to the coast on holiday. The distance is 1 200 km
and they must reach their destination in 12 hours. After 5
hours, they have travelled 575 km. Then one of their tyres
bursts. It takes 45 minutes to get the spare wheel on, before
they can drive again. At what average speed must they drive the
remainder of the journey to reach their destination on
time?
- The number of teachers
at a school has increased in the ratio 5 : 6. If there used to
be 25 teachers at the school, how many teachers are there
now?
- ABC for Life needs to
have their annual statements audited. They are quoted R8 500 +
14% VAT by Audits Inc. How much will ABC for Life have to pay
Audits Inc. in total?
- Reshmi invests R35 000
for three years at an interest rate of 8,2% per annum.
Determine how much money will be in her account at the end of
the investment period.
- Lesebo wants to buy a
lounge suite that costs R7 999 cash. He does not have enough
money and so decides to buy it on hire purchase. The store
requires a 15% deposit up front, and 18 monthly instalments of
R445.
- Calculate the deposit that Lesebo must
pay.
- How much extra does Lesebo pay because
he buys the lounge suite on hire purchase, rather than in
cash?
- Calculate the deposit that Lesebo must
pay.
- Consider the following
exchange rates table:
South African Rand
1.00 ZAR
inv. 1.00 ZAR
Euro
0.075370
13.267807
US Dollar
0.098243
10.178807
British Pound
0.064602
15.479409
Indian Rupee
5.558584
0.179902
Australian Dollar
0.102281
9.776984
Canadian Dollar
0.101583
9.844200
Emirati Dirham
0.360838
2.771327
Swiss Franc
0.093651
10.677960
Chinese Yuan Renminbi
0.603065
1.658195
Malaysian Ringgit
0.303523
3.294646
- Write down the amount in rand that needs
to be exchanged to get 1 Swiss franc. Give your answer to the
nearest cent.
- Write down the only currency for which
an exchange of R100 will give you more than 100 units of that
currency.
- Ntsako is travelling to Dubai and
converts R10 000 into Emirati dirhams. How many dirhams does
Ntsako receive (assume no commission)?
- Write down the amount in rand that needs
to be exchanged to get 1 Swiss franc. Give your answer to the
nearest cent.
Integers
Don't use a calculator for any of the questions in this section.
- Write a number in each
box to make the calculations correct.
- ☐ + ☐ = -11
- ☐ - ☐ = -11
- Fill <, > or =
into each block to show the relationships.
- -23 ☐ 20
- -345 ☐ -350
- \(4 - 3\) ☐ \(3 - 4\)
- \(5 - 7\) ☐ \(-(7 - 5)\)
- \(-9 \times 2\) ☐ \(-9 \times -2\)
- \( -4 \times 5\) ☐ \(4 \times -5\)
- \( -10 \div 5 ☐ -10 \div -2 \)
- \(-15 \times -15\) ☐ 224
- Follow the pattern to
complete the number sequences.
- 8; 5; 2;☐
- 2; -4; 8;☐
- -289; -293; -297;☐
- Look at the number
lines. In each case, the missing number is halfway between the
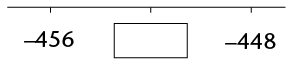
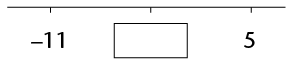
other two numbers. Fill in the correct values in the boxes.
-
- Calculate the following:
- \( -5 - 7\)
- \( 7 - 10\)
- \( 8-(-9)\)
- \( (-5)(-2)(-4)\)
- \( 5 + 4 \times 2\)
- \( \frac{(\sqrt{4})(-2)^2}{-4}\)
- \( \frac{-(-3)^3\sqrt[3]{125}}{(-9)(3)}\)
- \( \frac{\sqrt[3]{-64}}{-3-1}\)
- \( -5 - 7\)
-
- Write down two numbers that multiply
to give -15. (One of the numbers must be positive and the other
negative.)
- Write down two numbers that add to 15.
One of the numbers must be positive and the other negative.
- Write down two numbers that multiply
to give -15. (One of the numbers must be positive and the other
negative.)
- At 5 a.m., the
temperature in Kimberley was -3 °C. At 1 p.m., it
was 17 °C. By how many degrees had the temperature
risen?
- A submarine is 220 m
below the surface of the sea. It travels 75 m upwards. How far
below the surface is it now?
Exponents
You should not use a calculator for any of the questions in this section.
- Write down the value of
the following:
- \((-3)^3\)
- \(-5^2\)
- \( (-1)^{200}\)
- \( (10^2)^2\)
- \((-3)^3\)
- Write the following numbers in
scientific notation:
- 200 000
- 12,345
- 200 000
- Write the following numbers in
ordinary notation:
- \(1,3 \times 10^2 \)
- \(7,01 \times 10^7 \)
- \(1,3 \times 10^2 \)
- Which of the following numbers
is bigger: \(5,23 \times 10^{10}\) or \(2 ,9 \times 10^{11}\)?
- Simplify the
following:
- \(2^7 \times 2^3\)
- \(2x^3 \times 4x^4\)
- \((-8y^6) \div (4y^3)\)
- \((3x^8)^3\)
- \( (2x^5)(0.5x^{-5})\)
- \( (-3a^2b^3c)(-4abc^2)^2\)
- \( \frac{(2xy^2z^3)(-5y^2z)^2}{20xy^8z^4} \)
- \(2^7 \times 2^3\)
- Write down the values
of each of the following:
- \((0,6)^2\)
- \((0,2)^3\)
- \((\frac{1}{2})^5\)
- \(\sqrt{\frac{1}{4}}\)
- \(4\sqrt{\frac{9}{64}}\)
- \(\sqrt[3]{0.001}\)
- \((0,6)^2\)
Numeric and geometric patterns
- For each of the
following sequences, write the rule for the relationship
between each term and the following term in words. Then use the
rule to write the next three terms in the sequence.
- \(12; 7; 2;\text{______};\text{______};\text{______}\)
- \( -2; -6; -18;\text{______};\text{______};\text{______}\)
- \(100; -50; 25;\text{______};\text{______};\text{______}\)
- \(3; 4; 7; 11;\text{______};\text{______};\text{______}\)
- \(12; 7; 2;\text{______};\text{______};\text{______}\)
- In this question, you
are given the rule by which each term of the sequence can be
found. In all cases, \(n\) is the position of the
term.
Determine the first three terms of each of the sequences. (Hint: Substitute \(n = 1\) to find the value of the first term.)
- \(n \times 4\)
- \(n\times 5 - 12\)
- \(2 \times n^2\)
- \(3n \div 3 \times -2\)
- \(n \times 4\)
- Write down the rule by
which each term of the sequence can be found (in a similar
format to those given in question 2, where n is the position of the
term).
- \(2; 4; 6; ...\)
- \(-7; -3; 1; ...\)
- \(2; 4; 8; ...\)
- \( 9; 16; 23; ...\)
- \(2; 4; 6; ...\)
- Use the rules you have
found in question 3 to find the value of the 20th term of the
sequences in questions 3(a) and 3(b).
-
- Find the relationship
between the position of the term in the sequence and the value
of the term, and use it to fill in the missing values in the
tables.
-
Position in sequence
1
2
3
4
25
Value of the term
-8
-11
-14
-
Position in sequence
1
2
3
Value of the term
1
3
9
243
19 683
-
- The image below shows a
series of patterns created by matches.
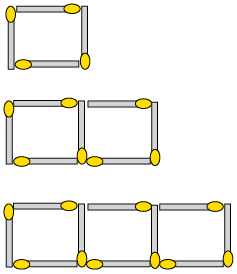
- Write in words the rule that describes
the number of matches needed for each new pattern.
- Use the rule to determine the missing
values in the table below, and fill them in.
Number of the pattern
1
2
3
4
20
Number of matches needed
4
7
151
- Write in words the rule that describes
the number of matches needed for each new pattern.
Functions and relationships
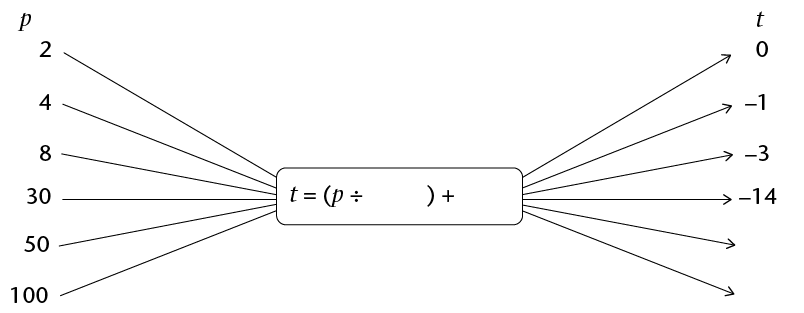
- Fill in the missing
input values, output values or rule in these flow diagrams.
Note that \(p\) and
\(t\) are integers.
-
- Consider the values in
the following table. The rule for finding \(y\) is: divide \(x\) by -2 and subtract 4. Use the
rule to determine the missing values in the table, and write
them in.
x
-2
0
2
5
y
-1
-3
-4
48
- Consider the values in
the following table:
\(x\)
-2
-1
0
1
2
4
15
\(y\)
1
3
5
7
9
61
- Write in words the rule for finding the
\(y\)-values in the
table.
- Use the rule to determine the missing
values in the table, and write them in.
- Write in words the rule for finding the
\(y\)-values in the
table.
Algebraic expressions
- Look at this algebraic
expression: \(5x^3 - 9 + 4x - 3x^2\).
- How many terms does this
expression have?
- What is the variable in
this expression?
- What is the coefficient of
the \(x^2\)
term?
- What is the constant in
this expression?
- Rewrite the expression so that the terms
are in order of decreasing powers of \(x\).
- How many terms does this
expression have?
- In this question, \(x=6\) and \(y = 17\). Complete
the rules to show different ways to determine \(y\) if \(x\) is known. The first way is
done for you:
Way 1: Multiply x by 2 and add 5. This can be written as \(y = 2x + 5\)
- Way 2: Multiply \(x\) by ______ and then subtract ______. This can be written as
- Way 3: Divide \(x\) by ______ and then add ______ . This can be written as
- Way 4: Add ______ to \(x\), and then multiply by ______ . This can be written as
- Way 2: Multiply \(x\) by ______ and then subtract ______. This can be written as
- Simplify:
- \(2x^2 + 3x^2\)
- \(9xy -12xy\)
- \(3y^2 - 4y + 3y - 2y^2\)
- \(9m^3 + 9m^2 + 9m^3 - 3\)
- \(2x^2 + 3x^2\)
- Calculate the value of the
following expressions if \(a = -2; b = 3; c = -1 \text{ and } d = 0:\)
- \(abc\)
- \(-a^2\)
- \((abc)^d\)
- \(a + b- 2c\)
- \((a + b)^{10}\)
- \(abc\)
Algebraic equations
- Write equations that represent
the given information:
- Nandi is \(x\) years old. Shaba, who is
\(y\) years old, is three years older than Nandi.
- The temperature at Colesberg during the
day was \(x\)°C. But at night, the temperature dropped by 15
degrees to reach -2°C.
- Nandi is \(x\) years old. Shaba, who is
\(y\) years old, is three years older than Nandi.
- Solve the following equations
for \(x\):
- \(x + 5 = 2\)
- \(7 - x = 9\)
- \(3x - 1 = -10\)
- \(2x^3 = -16\)
- \( 2^x = 16\)
- \( 2(3)^x = 6\)
- \(x + 5 = 2\)
- If \(3n - 1 = 11\), what is the value
of \(4n\)?
- If \(c = a + b\) and \(a + b + c = 16\) , determine the value of
\(c\).
-
- If \(2a + 3 = b\), write down values for \(a\) and \(a\) that will make the equation
true.
- Write down a different pair of values to
make the equation true.
- If \(2a + 3 = b\), write down values for \(a\) and \(a\) that will make the equation
true.
Assessment
In this section, the numbers in brackets at the end of a question indicate the number of marks the question is worth. Use this information to help you determine how much working is needed. The total number of marks allocated to the assessment is 60.
- The profits
of GetRich Inc. have decreased in the ratio 5 : 3 due to the
recession in the country. If their profits used to be R1 250
000, how much are their profits now?
- Which car
has the better rate of petrol consumption: Ashley's car, which
drove 520 km on 32â„“ of petrol,
or Zaza's car, which drove 880 km on 55â„“ of petrol? Show all your
working.
- Hanyani
took out a R25 000 loan from a lender that charges him 22%
interest each year. How much will he owe in one year's time?
- Consider the following
exchange rates table:
South African Rand
1.00 ZAR
inv. 1.00 ZAR
Indian Rupee
5.558584
0.179902
Australian Dollar
0.102281
9.776984
Canadian Dollar
0.101583
9.844200
Emirati Dirham
0.360838
2.771327
Chinese Yuan Renminbi
0.603065
1.658195
Malaysian Ringgit
0.303523
3.294646
Chen returns from a business trip to Malaysia with 2 500 ringgit in his wallet. If he changes this money into rand in South Africa, how much will he receive?
- Fill <, > or =
into the block to show the relationship between the number
expressions:
- \(6 - 4\) ☐ \(4 - 6\)
- \(2 \times -3\) ☐ \(-3^2\)
- Look at the
number sequence below. Fill in the next term into the
block.
\(-5; 10; -20\);☐
- Calculate the following:
- \( (-4)^2 - 20\)
- \(\sqrt[3]{-8} + 14 \ \div 2\)
- \( (-4)^2 - 20\)
- Julius
Caesar was a Roman emperor who lived from 100 BC to 44 BC. How
old was he when he died?
-
- Write down two numbers
that divide to give an answer of -8. One of the numbers must be
positive, and the other negative.
- Write down two numbers that
subtract to give an answer of 8. One of the numbers must be
positive and the other negative.
- Write down two numbers
that divide to give an answer of -8. One of the numbers must be
positive, and the other negative.
- Write the
following number in scientific notation: 17 million.
- Which of
the following numbers is bigger: \(3,47 \times 10^{21} \text{ or }7,99 \times
10^{20}\)?
- Simplify the
following, leaving all answers with positive exponents:
- \( 3^7
\times 3^-2\)
- \((-12y^8) \div
(-3y^2)\)
- \(
\frac{(3xy^2z^3)(-yz)^2}{15x^5y^4z^7}\)
- \( 3^7
\times 3^-2\)
- Write down the values
of each of the following:
- \((0.3)^3\)
- \( 8
\sqrt{\frac{25}{16}} \)
- \((0.3)^3\)
- Consider the following number
sequence: \(2; -8; 32; ...\)
- Write in words the rule by
which each term of the sequence can be found.
- Write the next three terms in
this sequence.
- Write in words the rule by
which each term of the sequence can be found.
- The picture below shows a
series of patterns created by matches.
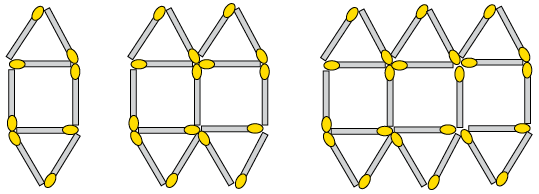
- Write a formula for the rule
that describes the relationship between the number of matches
and the position of the term in the sequence (pattern number).
Let \(n\) be the
position of the term.
- Use the rule to determine the
values of \(a\) to \(c\) in the following table:
Number of the pattern
1
2
3
4
15
c
Number of matches needed
8
15
22
a
b
148
- Write a formula for the rule
that describes the relationship between the number of matches
and the position of the term in the sequence (pattern number).
Let \(n\) be the
position of the term.
- Consider the values in
the following table:
x
-2
-1
0
1
2
5
12
y
-7
-4
-1
2
5
98
- Write in words the rule for
finding the \(y\)-values in the table.
- Use the rule to determine the
missing values in the table, and fill them in.
- Write in words the rule for
finding the \(y\)-values in the table.
- . Simplify:
- \(2z^2 - 3z^2\)
- \( 8y^2 - 6y + 4y - 7y^2\)
- \(2z^2 - 3z^2\)
- Determine
the value of \(2a^2 - 10\) if \(a = -2\).
- If \(c + 2d = 27\), give the value of the
following:
- \(2c + 4d\)
- \(\frac{c +
2d}{-9}\)
- \(\sqrt[3]{c + 2d}\)
- \(2c + 4d\)
- Solve the
following for \(x\): (5)
- \(-x - 11\)
- \(2x -5 = - 11\)
- \(4x^3 = 32\)
- \(-x - 11\)