In this chapter you will learn about quantities that change, such as the height of a tree. As the tree grows, the height changes. A quantity that changes is called a variable quantity or just a variable.
It is often the case that when one quantity changes, another quantity also changes. For example, as you make more and more calls on a phone, the total cost increases. In this case, we say there is a relationship between the amount of money you have to pay and the number of calls you make. You will learn how to describe a relationship between two quantities in different ways.
Constant and variable quantities
Looking for connections between quantities
Consider the following seven situations. There are two quantities in each situation. For each quantity, state whether it is constant (always the same number) or whether it changes. Also state, in each case, whether one quantity has an influence on the other. If it has, try to say how the one quantity will influence the other quantity.
- Your age and the number of fingers on your hands
- The number of calls you make and the airtime left on your cellphone
- The length of your arm and your ability to finish Mathematics tests quickly
- The number of identical houses to be built and the number of bricks required
- The number of learners at a school and the length of the school day
- The number of learners at a school and the number of classrooms needed
- The number of matches in each arrangement here, and the number of triangles in the arrangement

A quantity that changes is called a variable quantity or just a variable.
If one variable quantity is influenced by another, we say there is a relationship between the two variables. It is sometimes possible to find out what value of the one quantity, in other words what number, is linked to a specific value of the other quantity.
-
- Look at the match arrangements in
question 7. If you know that there are 3 triangles in an
arrangement, can you say with certainty how many matches there
are in that specific arrangement?
- How many matches are there
in the arrangement with 10 triangles?
- Is there another possible answer for
question (b)?
- Look at the match arrangements in
question 7. If you know that there are 3 triangles in an
arrangement, can you say with certainty how many matches there
are in that specific arrangement?
- Complete the flow
diagram by filling in all the missing numbers. Do you see any
connections between the situation in question 7 and this flow
diagram? If so, describe the connections.
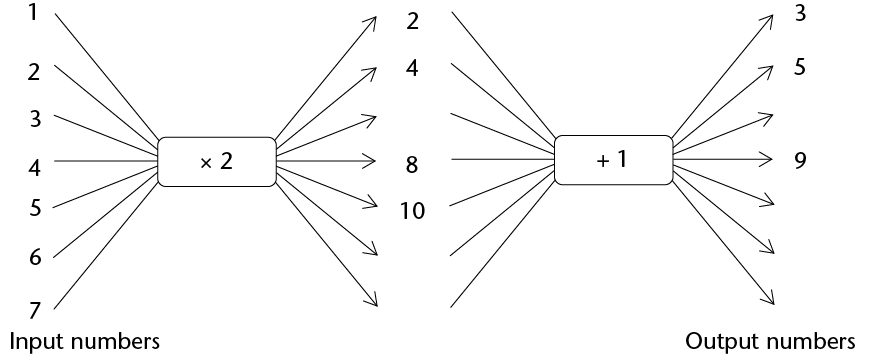
Completing some flow diagrams
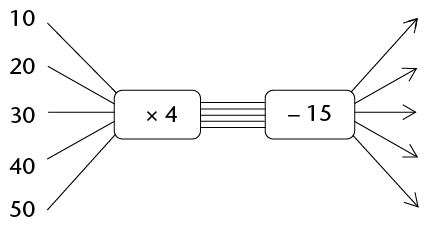
A relationship between two quantities can be shown with a flow diagram, such as those below. Unfortunately, only some of the numbers can be shown on a flow diagram.
- Calculate the output
numbers for the flow diagram below. Some input numbers are
missing. Choose and insert your own input numbers.
Each input number in a flow diagram has a corresponding output number. The first (top) input number corresponds to the first output number. The second input number corresponds to the second output number and so on.
We call +5 the operator.
-

- What type of numbers are the given input
numbers?
- In the above flow diagram, the output
number 8 corresponds to the input number 3. Complete the
following sentences:
In the relationship shown in the above flow diagram, the output number ______ corresponds to the input number -1.
The input number ______ corresponds to the output number 7.
If more places are added to the flow diagram, the input number ______ will correspond to the output number 31.
-
-
- Complete this flow diagram.

- Compare this flow diagram to the flow
diagram in question 1. What link do you find between the
two?
- Complete this flow diagram.
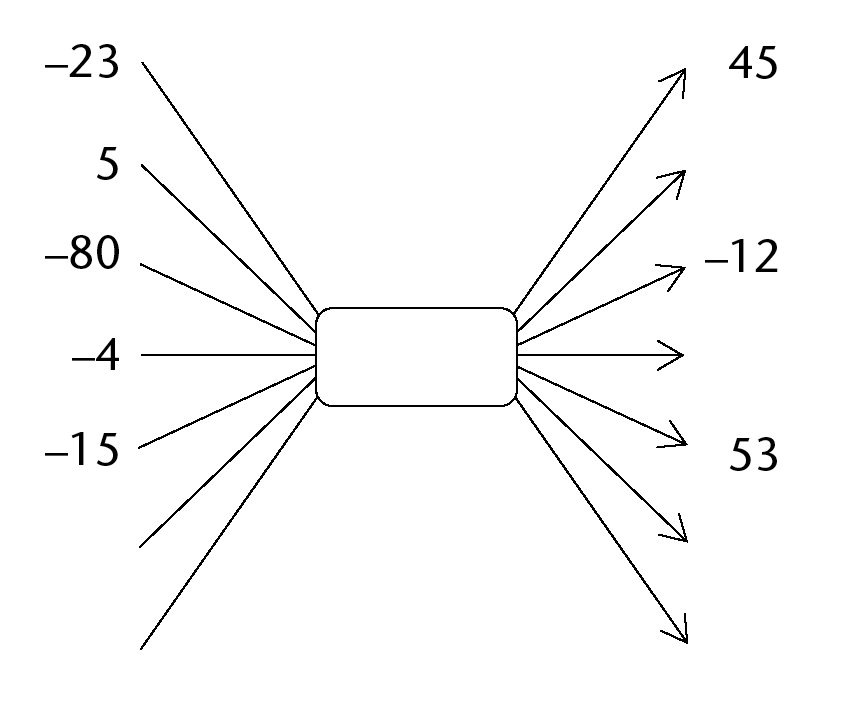
- Complete the flow
diagrams below. You have to find out what the operator
for (b) is, and fill it in yourself.
-
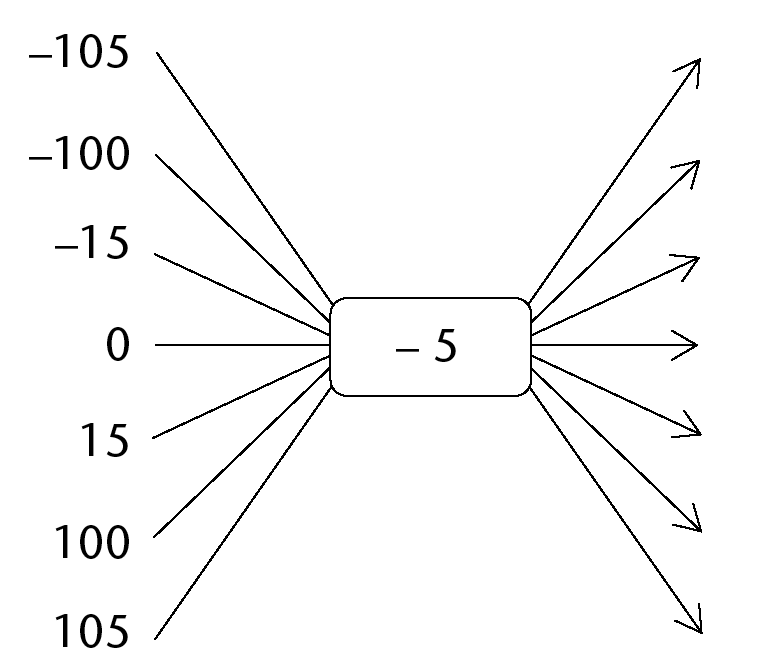
-
- What number can you add in
(a), instead of subtracting 5, that will produce the same
output numbers?
- What number can you subtract in (b),
instead of adding a number, that will produce the same output
numbers?
-
- Complete the flow diagram:
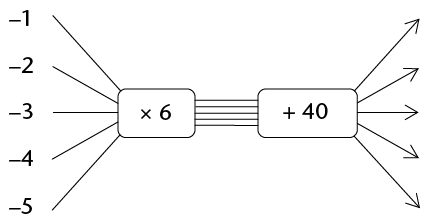
A completed flow diagram shows two kinds of information:
- It shows what calculations are done to produce the output numbers.
- It shows which output number is connected to which input number.
The flow diagram that you have completed in question 4 shows the following information:
- Each input number is multiplied by 6, then 40 is added to produce the output numbers.
- The input and output numbers are connected as shown in the table below.
|
Input numbers |
-1 |
-2 |
-3 |
-4 |
-5 |
|
Output numbers |
34 |
28 |
22 |
16 |
10 |
-
- Describe in words how the output
numbers below can be calculated.
- Use the table below to show which output
numbers are connected to which input numbers in the above flow
diagram.
- Describe in words how the output
numbers below can be calculated.
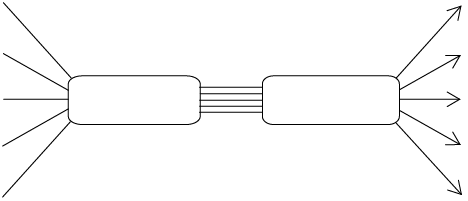
- The following
information is available about the floor space and cost of new
houses in a new development. The cost of an empty stand is R180
000.
Floor space in square metres
90
120
150
180
210
Cost of house and stand
540 000
660 000
780 000
900 000
1 020 000
- Represent the above information on the
flow diagram below.
- Show what the houses only will cost, if
you get the stand for free.

- Try to figure out what the cost of a
house and stand will be, if there are exactly one hundred 1 m
by 1 m sections of floor space in the house.
- Represent the above information on the
flow diagram below.
Different ways to describe relationships
A relationship between red dots and blue dots
Here is an example of a relationship between two quantities:

In each arrangement there are some red dots and some blue dots.
- How many blue dots are there
if there is one red dot?
- How many blue dots are there
if there are two red dots?
- How many blue dots are there
if there are three red dots?
- How many blue dots are there
if there are four red dots?
- How many blue dots are there
if there are five red dots?
- How many blue dots are there
if there are six red dots?
- How many blue dots are there
if there are seven red dots?
- How many blue dots are there
if there are ten red dots?
- How many blue dots are there
if there are twenty red dots?
- How many blue dots are there
if there are one hundred red dots?
-
Which of the descriptions correctly
describe the relationship between the number of blue dots and
the number of red dots in the above arrangements? Test each
description thoroughly for all the above arrangements. List
them on the dotted line below. Write only the letters, for
example (d).
Something to think about
Are there different possibilitiesfor the number of blue dots if there are 3 red dots in the arrangement?
Are there different possibilities for the number of blue dots if there are 2 red dots in the arrangement?
Are there different possibilities for the number of blue dots if there are 20 red dots in the arrangement?
- the number of red dots
 the number of blue dots
the number of blue dots - to calculate the number of blue dots you multiply the number of red dots by 2, add 1 and multiply the answer by 2
- number of blue dots = 2 \(\times\) the number of red dots + 4
-
Number of red dots
1
2
3
4
5
6
Number of blue dots
6
10
14
18
22
26
-
-
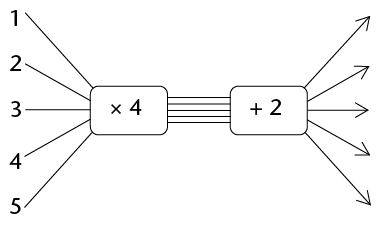
- number of blue dots = 4 \(\times\) the number of red dots + 2
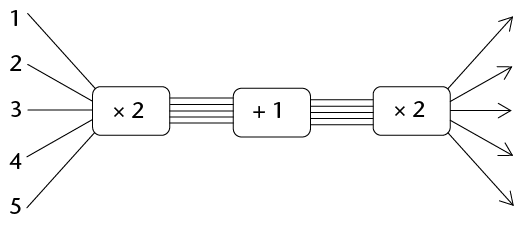
- number of blue dots \(= 2 \times (2 \times\) the number of red dots + 1) (Remember that the calculations inside the brackets are done first.)
- the number of red dots
The descriptions in (c), (g) and (h) above are called word formulae.
Translating between different languages of description
A relationship between two quantities can be described in different ways, including the following:
- a table of values of the two quantities
- a flow diagram
- a word formula
- a symbol formula (or symbolic formular)
You will learn about symbolic formulae in section 5.3.
- The relationship between two
quantities is described as follows:
The second quantity is always 3 times the first quantity plus 8.
The first quantity varies between 1 and 5, and it is always a whole number.
- Describe this relationship with the flow
diagram.
- Describe the relationship between the
two quantities with this table.
- Describe the relationship between the
two quantities with a word formula.
- Describe this relationship with the flow
diagram.
- The relationship between two
quantities is described as follows:
The input numbers are the first five odd numbers.
value of the one quantity
 the
corresponding value of the other quantity
the
corresponding value of the other quantity- Describe this relationship with a
table.
- Describe the relationship with a word
formula.
- Describe this relationship with a
table.
Algebraic symbols for variables and relationships
Describing procedures in different ways
- In each case do four
things:
- Complete the table.
- Describe the relationship with a word formula.
- Describe the input numbers in words.
- Describe the output numbers in words.
- input number
 output number
output number
Input number
5
10
15
20
25
30
Output number
the output number =
- input number
 output number
output number
Input number
5
10
15
20
25
30
Output number
- input number
 output number
output number
Input number
5
10
15
20
25
30
Output number
Formulae with symbols
Instead of writing "input number" and "output number" in formulae, one may just write a single letter symbol as an abbreviation.
Mathematicians have long ago adopted the convention of using the letter symbol \(x\) as an abbreviation for "input number", and the letter symbol \(y\) as an abbreviation for "output number".
Other letter symbols than \(x\) and \(y\) are also used to indicate variable quantities.
The word formula you wrote for question 1(a) can be written more shortly as
\( y = 10 \times x + 15 \)
Mathematicians have also long ago agreed that one may leave the \times-sign out when writing symbolic formulae.
So, instead of \( y = 10 \times x + 15 \) we may write \( y = 10x + 15 \).
It is not at all wrong to use the multiplication sign in symbolic formulae.
- Rewrite your word formulae in
questions 1(b) and 1(c) as symbolic formulae.
- Write a word formula for each
of the following relationships:
- \(y = 7x + 10\)
- \(y = 7(x + 10)\)
- \(y = 7(2x + 10)\)
- \(y = 7x + 10\)
Writing symbolic formulae
Describe each of the following relationships with a symbolic formula:
- To calculate the
output number, the input number is multiplied by 4 and 7 is
subtracted from the answer.
- To calculate the
output number, 7 is subtracted from the input number and the
answer is multiplied by 5.
- To calculate the
output number, 7 is subtracted from the input number, the
answer is multiplied by 5 and 3 is added to this answer.
