In this chapter you will learn to create, recognise, describe, extend and make generalisations about numeric and geometric patterns. Patterns allow us to make predictions. You will also work with different representations of patterns, such as flow diagrams and tables.
The term-term relationship in a sequence
Going from one term to the next
A list of numbers which form a pattern is called a sequence. Each number in a sequence is called a term of the sequence. The first number is the first term of the sequence.
Write down the next three numbers in each of the sequences below. Also explain in writing, in each case, how you figured out what the numbers should be.
- Sequence A: 2; 5; 8; 11; 14; 17; 20; 23;
- Sequence B: 4; 5; 8; 13; 20; 29; 40;
- Sequence C: 1; 2; 4; 8; 16; 32; 64;
- Sequence D: 3; 5; 7; 9; 11; 13; 15; 17; 19;
- Sequence E: 4; 5; 7; 10; 14; 19; 25; 32; 40;
- Sequence F: 2; 6; 18; 54; 162; 486;
- Sequence G: 1; 5; 9; 13; 17; 21; 25; 29; 33;
- Sequence H: 2; 4; 8; 16; 32; 64;
Numbers that follow one another are said to be consecutive.
Adding or subtracting the same number
- Which sequences on the previous section are of the same kind as sequence A? Explain your answer.
Amanda explains how she figured out how to continue sequence A:
I looked at the first two numbers in the sequence and saw that I needed 3 to go from 2 to 5. I looked further and saw that I also needed 3 to go from 5 to 8. I tested that and it worked for all the next numbers.
This gave me a rule I could use to extend the equence: add 3 to each number to find the next number in the pattern.
Tamara says you can also find the pattern by working backwards and subtracting 3 each time:
When the differences between consecutive terms of a sequence are the same, we say the difference is constant.
\[14 - 3 = 11; 11 - 3 = 8; 8 - 3 = 5; 5 - 3 = 2\]
-
Provide a rule to describe the relationship between the numbers in the sequence.
Use this rule to calculate the missing numbers in the sequence.
- 1; 8; 15;______;______;______;______;______;...
- 10 020;______;______;______; 9 980; 9 970;______; 9 940; 9 930; ...
- 1,5; 3,0; 4,5;______;______;______;______;______;...
- 2,2; 4,0; 5,8;______;______;______;______;______;...
- \( 45; \frac{3}{4}; 46; \frac{3}{4}; 47; \frac{1}{2}; 48;\text{______;______;______;______;______;}
\)...
- ______; 100,49; 100,38; 100,27; ______;______; 99,94; 99,83; 99,72;...
- 1; 8; 15;______;______;______;______;______;...
- Complete the table below.
Input number
1
2
3
4
5
12
n
Input number + 7
8
11
15
30
Multiplying or dividing with the same number
Take another look at sequence F: 2; 6; 18; 54; 162; 486; ...
Piet explains that he figured out how to continue the sequence F:
I looked at the first two terms in the sequence and wrote \(2 \times ? = 6\).
When I multiplied the first number by 3, I got the second number: \(2 \times 3 = 6\).
I then checked to see if I could find the next number if I multiplied 6 by 3: \(6 \times 3 = 18\).
I continued checking in this way: \( 18 \times 3 = 54; 54 \times 3 = 162\) and so on.
This gave me a rule I can use to extend the sequence and my rule was: multiply each number by 3 to calculate the next number in the sequence.
Zinhle says you can also find the pattern by working backwards and dividing by 3 each time:
\[ 54 \div 3 = 18; 18 \div 3 = 6;6 \div 3= 2\]
The number that we multiply with to get the next term in the sequence is called a ratio. If the number we multiply with remains the same throughout the sequence, we say it is a constant ratio.
- Check whether Piet's reasoning works for sequence H: 2; 4; 8; 16; 32; 64; ...
- Describe, in words, the rule for finding the next number in the sequence. Also write down the next five terms of the sequence if the pattern is continued.
- 1; 10; 100; 1 000;
- 16; 8; 4; 2;
- 7; -21; 63; -189;
- 3; 12, 48;
- 2 187; -729; 243; -81;
- 1; 10; 100; 1 000;
-
- Fill in the missing output and input numbers:
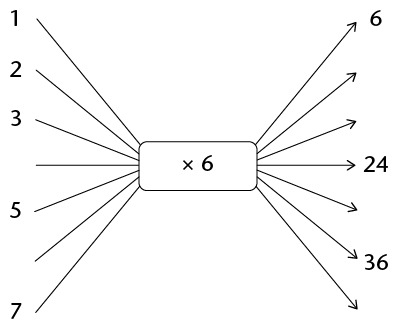
What is the term-to-term rule for the output numbers here, \(+ 6 \text{ or } \times 6?\)
- Complete the table below:
Input numbers
1
2
3
4
5
12
x
Output numbers
6
24
36
- Fill in the missing output and input numbers:
Neither adding nor multiplying by the same number
- Consider sequences A to H again and answer the questions that follow:
Sequence A: 2; 5; 8; 11; 14; 17; 20; 23; ...
Sequence B: 4; 5; 8; 13; 20; 29; 40;...
Sequence C: 1; 2; 4; 8; 16; 32; 64;...
Sequence D: 3; 5; 7; 9; 11; 13; 15; 17; 19; ...
Sequence E: 4; 5; 7; 10; 14; 19; 25; 32; 40;...
Sequence F: 2; 6; 18; 54; 162; 486;...
Sequence G: 1; 5; 9; 13; 17; 21; 25; 29; 33;...
Sequence H: 2; 4; 8; 16; 32; 64;...
- Which other sequence(s) is/are of the same kind as sequence B? Explain.
- In what way are sequences B and E different from the other sequences?
- Which other sequence(s) is/are of the same kind as sequence B? Explain.
There are sequences where there is neither a constant difference nor a constant ratio between consecutive terms and yet a pattern still exists, as in the case of sequences B and E.
- Consider the sequence: 10; 17; 26; 37; 50; ...
- Write down the next five numbers in the sequence.
- Eric observed that he can calculate the next term in the sequence as follows: 10 + 7 = 17; 17 + 9 = 26; 26 + 11 = 37. Use Eric's method to check whether your numbers in question (a) above are correct.
- Write down the next five numbers in the sequence.
- Which of the statements below can Eric use to describe the relationship between the numbers in the sequence in question 2? Test the rule for the first three terms of the sequence and then simply write "yes" or "no" next to each statement.
- Increase the difference between consecutive terms by 2 each time
- Increase the difference between consecutive terms by 1 each time
- Add two more than you added to get the previous term
- Increase the difference between consecutive terms by 2 each time
- Provide a rule to describe the relationship between the numbers in the sequences below. Use your rule to provide the next five numbers in the sequence.
- 1; 4; 9; 16; 25;
- 2; 13; 26; 41; 58;
- 4; 14; 29; 49; 74;
- 5; 6; 8; 11; 15; 20;
- 1; 4; 9; 16; 25;
The position-term relationship in a sequence
Using position to make predictions
- Take another look at equences A to H. Which sequence(s) are of the same kind as sequence A? Explain.
Sequence A: 2; 5; 8; 11; 14; 17; 20; 23;...
Sequence B: 4; 5; 8; 13; 20; 29; 40;...
Sequence C: 1; 2; 4; 8; 16; 32; 64;...
Sequence D: 3; 5; 7; 9; 11; 13; 15; 17; 19;...
Sequence E: 4; 5; 7; 10; 14; 19; 25; 32; 40;...
Sequence F: 2; 6; 18; 54; 162; 486; ...
Sequence G: 1; 5; 9; 13; 17; 21; 25; 29; 33;...
Sequence H: 2; 4; 8; 16; 32; 64;...
Sizwe has been thinking about Amanda and Tamara's explanations of how they worked out the rule for sequence A and has drawn up a table. He agrees with them but says that there is another rule that will also work. He explains:
My table shows the terms in the sequence and the difference between consecutive terms:
|
1st term |
2nd term |
3rd term |
4th term |
||||||||||||||||||
|
A: |
5 |
8 |
11 |
14 |
|||||||||||||||||
|
differences |
+3 |
+3 |
+3 |
+3 |
+3 |
+3 |
+3 |
+3 |
+3 |
||||||||||||
Sizwe reasons that the following rule will also work:
Multiply the position of the number by 3 and add 2 to the answer.
I can write this rule as a number sentence: Position of the number\(\bf{ \times 3 + 2}\)
I use my number sentence to check: \( {\bf1} \times 3 + 2 = 5; {\bf2} \times 3 + 2 = 8; {\bf3} \times 3 + 2 = 11 \)
-
- What do the numbers in bold in Sizwe's number sentence stand for?
- What does the number 3 in Sizwe's number sentence stand for?
- What do the numbers in bold in Sizwe's number sentence stand for?
- Consider the sequence 5; 8; 11; 14; ...
Apply Sizwe's rule to the sequence and determine:
- term number 7 of the sequence
- term number 10 of the sequence
- the 100th term of the sequence
- term number 7 of the sequence
- Consider the sequence: 3; 5; 7; 9; 11; 13; 15; 17; 19;..
- Use Sizwe's explanation to find a rule for this sequence.
- Determine the 28th term of the sequence.
- Use Sizwe's explanation to find a rule for this sequence.
More predictions
Complete the tables below by calculating the missing terms.
-
Position in sequence
1
2
3
4
10
54
Term
4
7
10
13
-
Position in sequence
1
2
3
4
8
16
Term
4
9
14
19
-
Position in sequence
1
2
3
4
7
30
Term
3
15
27
- Use the rule Position in the sequence \(\times\) (position in the sequence + 1) to complete the table below.
Position in sequence
1
2
3
4
5
6
Term
2
Investigating and extending geometric patterns
Square numbers
A factory makes window frames. Type 1 has one windowpane, type 2 has four windowpanes, type 3 has nine windowpanes, and so on.
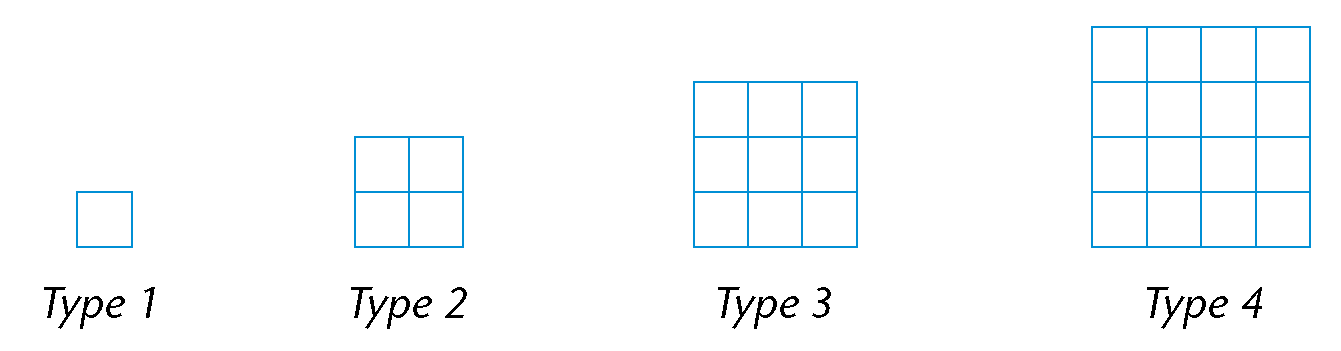
- How many windowpanes will there be in type 5?
- How many windowpanes will there be in type 6?
- How many windowpanes will there be in type 7?
- How many windowpanes will there be in type 12? Explain.
- Complete the table. Show your calculations.
Frame type
1
2
3
4
15
20
Number of windowpanes
1
4
9
16
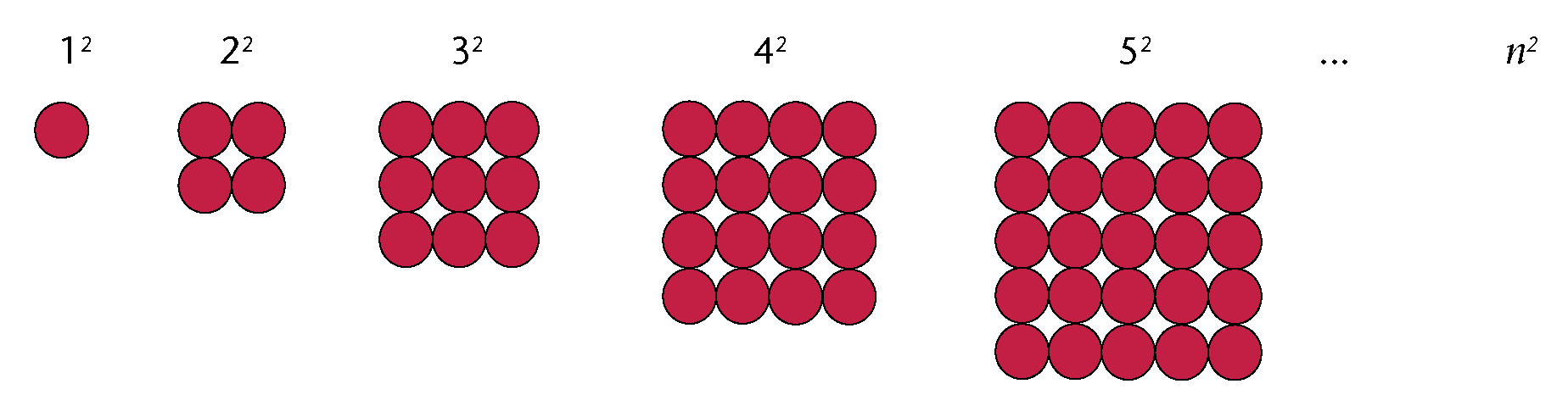
The symbol n is used below to represent the position number in the expression that gives the rule (\(n^2\)) when generalising.
In algebra we think of a square as a number that is obtained by multiplying a number by itself. So 1 is also a square because \(1 \times 1 = 1\).
Triangular numbers
Therese uses circles to form a pattern of triangular shapes:

- If the pattern is continued, how many circles must Therese have
- in the bottom row of picture 5?
- in the second row from the bottom of picture 5?
- in the third row from the bottom of picture 5?
- in the second row from the top of picture 5?
- in the top row of picture 5?
- in total in picture 5? Show your calculation.
- in the bottom row of picture 5?
- How many circles does Therese need to form triangle picture 7? Show the calculation.
- How many circles does Therese need to form triangle picture 8?
- Complete the table below. Show all your work.
Picture number
1
2
3
4
5
6
12
15
Number of circles
1
3
6
10
More than 2 500 years ago, Greek mathematicians already knew that the numbers 3, 6, 10, 15 and so on could form a triangular pattern. They represented these numbers with dots which they arranged in such a way that they formed equilateral triangles, hence the name triangular numbers. Algebraically we think of them as sums of consecutive natural numbers starting with 1.
Let us revisit the activity on triangular numbers that we did in the previous section.

So far, we have determined the number of circles in the pattern by adding consecutive natural numbers. If we were asked to determine the number of circles in picture 200, for example, it would take us a very long time to do so. We need to find a quicker method of finding any triangular number in the sequence.
Consider the arrangement below.

We have added the yellow circles to the original blue circles and then rearranged the circles in such a way that they are in a rectangular form.
- Picture 2 is 3 circles long and 2 circles wide. Complete the following sentences:
- Picture 3 is ______ circles long and ______ circles wide.
- Picture 1 is ______ circles long and ______ circle wide.
- Picture 4 is ______ circles long and ______ circles wide.
- Picture 5 is ______ circles long and ______ circles wide.
- How many circles will there be in a picture that is:
- 10 circles long and 9 circles wide?
- 7 circles long and 6 circles wide?
- 6 circles long and 5 circles wide?
- 20 circles long and 19 circles wide?
- 10 circles long and 9 circles wide?
Suppose we want to have a quicker method to determine the number of circles in picture 15. We know that picture 15 is 16 circles long and 15 circles wide. This gives a total of \(15 \times 16 = 240\) circles. But we must compensate for the fact that the yellow circles were originally not there by halving the total number of circles. In other words, the original figure has \(240 \div 2 = 120\) circles.
- Use the above reasoning to calculate the number of circles in:
- picture 20
- picture 35
- picture 20
Describing patterns in different ways
T-shaped numbers
The pattern below is made from squares.
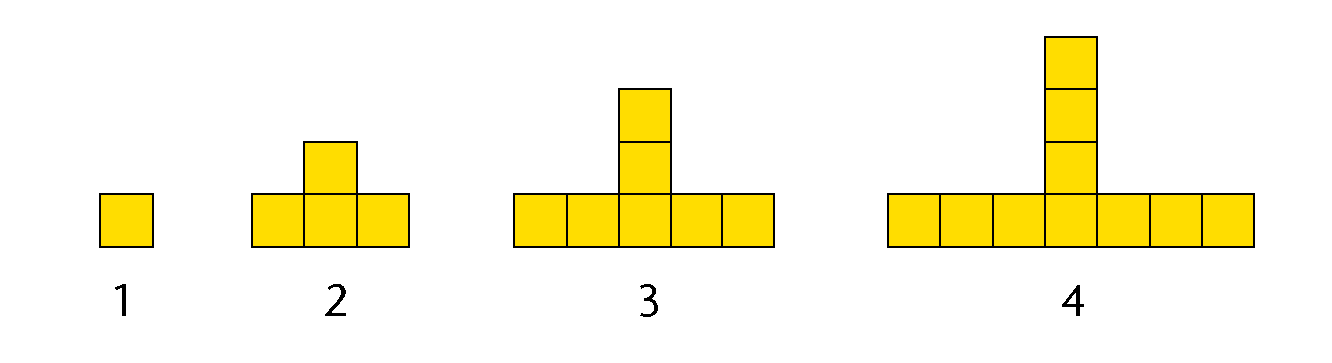
-
- How many squares will there be in pattern 5?
- How many squares will
there be in pattern 15?
- Complete the table.
Pattern number
1
2
3
4
5
6
20
Number of squares
1
4
7
10
- How many squares will there be in pattern 5?
Below are three different methods or plans to calculate the number of squares for pattern 20. Study each one carefully.
Plan A:
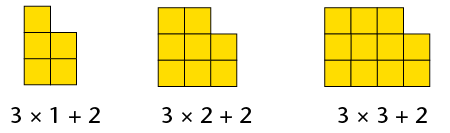
To get from 1 square to 4 squares, you have to add 3 squares. To get from 4 squares to 7 squares, you have to add 3 squares. To get from 7 squares to 10 squares, you have to add 3 squares. So continue to add 3 squares for each pattern until pattern 20.
Plan B:
Multiply the pattern number by 3, and subtract 2. So pattern 20 will have \(20 \times 3 - 2\) squares.
Plan C:
The number of squares in pattern 5 is 13. So pattern 20 will have \(13 \times 4 = 52\) squares because \(20 = 5 \times 4\).
-
- Which method or plan (A, B or C) will give the right answer? Explain why.
- Which of the above plans did you use? Explain why?
- Can this flow diagram be used to calculate the number of squares?
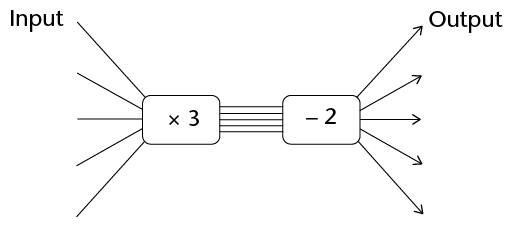
- Which method or plan (A, B or C) will give the right answer? Explain why.
... and some other shapes
- Three figures are given below. Draw the next figure in the tile pattern.

-
- If the pattern is continued, how many tiles will there be in the 17th figure? Answer this question by analysing what happens.
- Thato decides that it easier for him to see the pattern when the tiles are rearranged as shown here:
Use Thato's method to determine the number of tiles in the 23rd figure.
- Complete the flow diagram below by writing the appropriate operators so that it can be used to calculate the number of tiles in any figure of the pattern.
- How many tiles will there be in the 50th figure if the pattern is continued?
- If the pattern is continued, how many tiles will there be in the 17th figure? Answer this question by analysing what happens.
- Write down the next four terms in each sequence. Also explain, in each case, how you figured out what the terms are.
- 2; 4; 8; 14; 22; 32; 44;
- 2; 6; 18; 54; 162;
- 1; 7; 13; 19; 25;
- 2; 4; 8; 14; 22; 32; 44;
-
- Complete the table below by calculating the missing terms.
Position in sequence
1
2
3
4
5
7
10
Term
3
10
17
- Write the rule to calculate the term from the position in the sequence in words.
- Complete the table below by calculating the missing terms.
- Consider the stacks below.

- How many cubes will there be in stack 5?
- Complete the table.
Stack number
1
2
3
4
5
6
10
Number of cubes
1
8
27
- Write down the rule to calculate the number of cubes for any stack number.
- How many cubes will there be in stack 5?
