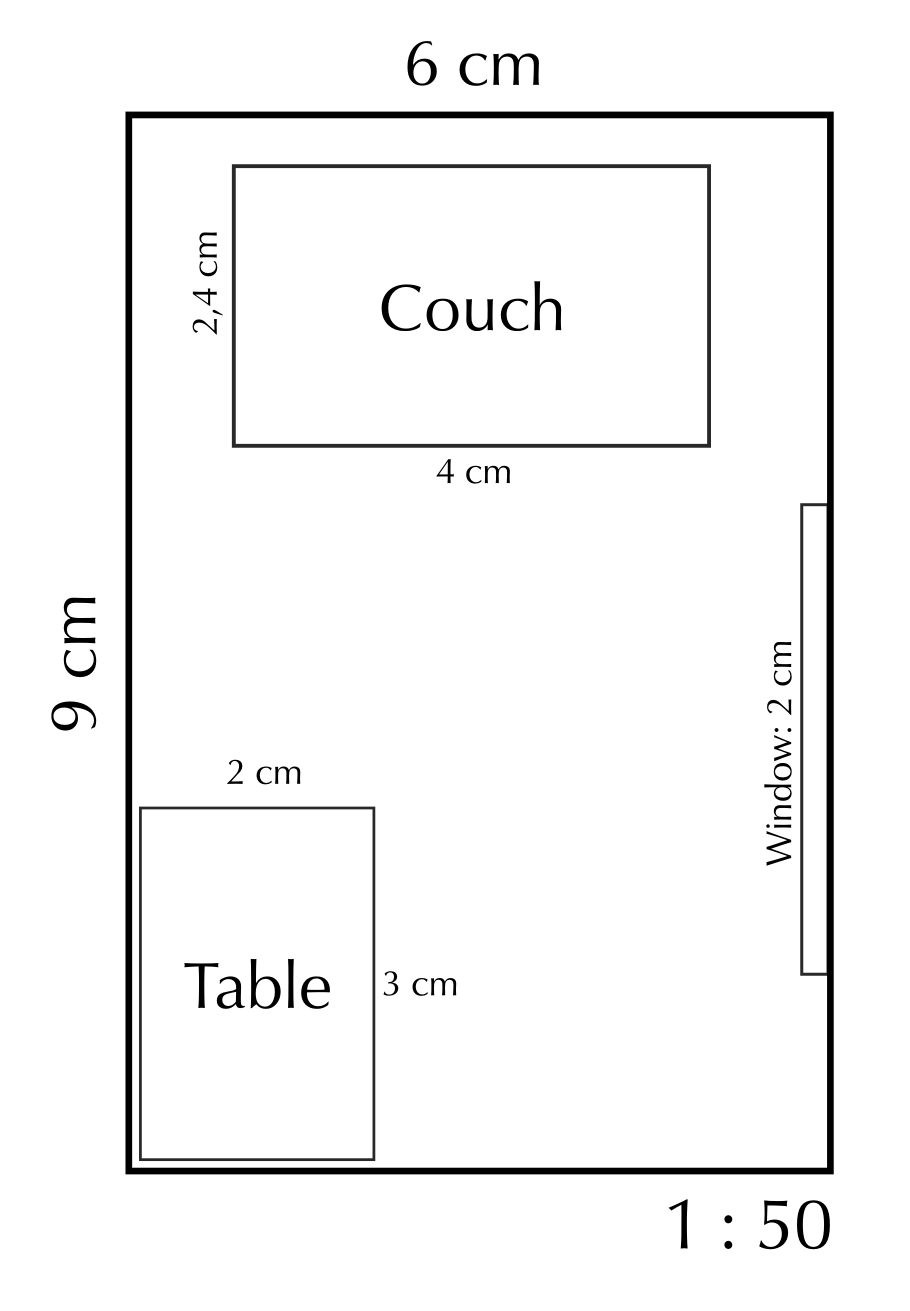
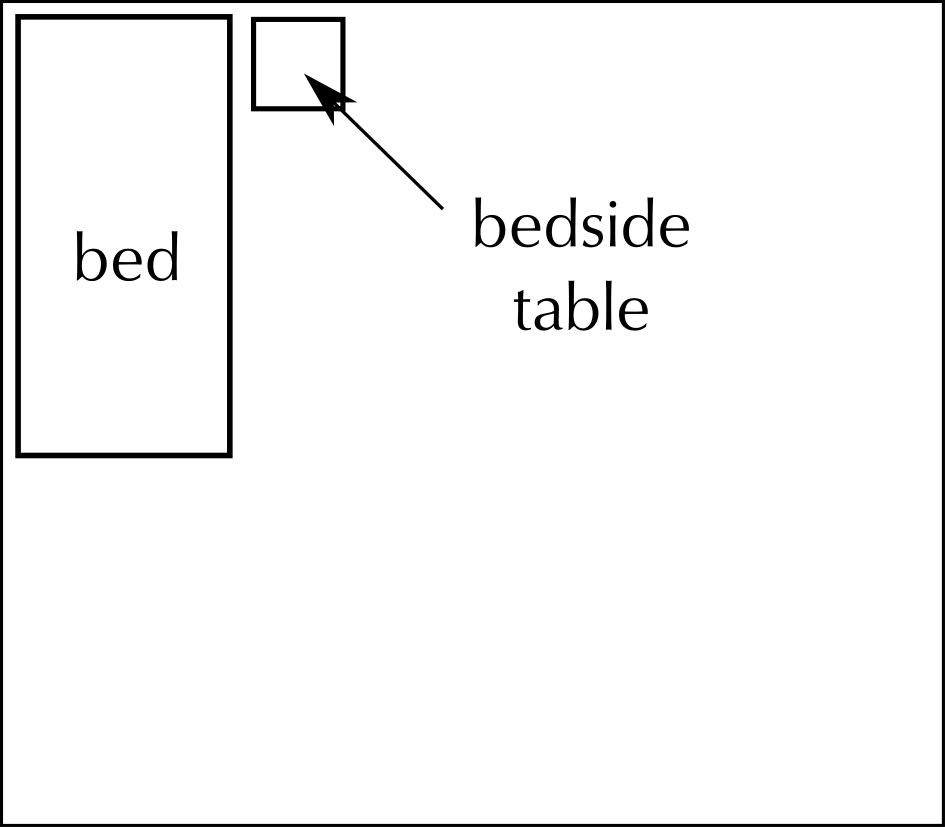
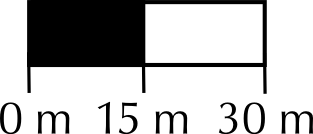The bedroom in the picture is \(\text{3,5}\) \(\text{m}\) by \(\text{4}\) \(\text{m}\). It has a standard sized single bed of \(\text{92}\) \(\text{cm}\) by \(\text{188}\) \(\text{cm}\). The bedside table is \(\text{400}\) \(\text{mm}\) square. Draw a floor plan to show the layout of the room. Use the number scale \(\text{1}\) : \(\text{50}\).
Room real measurements:
width \(\text{3,5}\) \(\text{m}\) = \(\text{350}\) \(\text{cm}\)
length \(\text{4}\) \(\text{m}\) = \(\text{400}\) \(\text{cm}\)
Scale drawing:
\(\text{350}\) \(\div\) \(\text{50}\) = \(\text{7}\) \(\text{cm}\)
\(\text{400}\) \(\div\) \(\text{40}\) = \(\text{8}\) \(\text{cm}\)
Bed real measurements:
Width = \(\text{92}\) \(\text{cm}\)
Length = \(\text{188}\) \(\text{cm}\)
Scale drawing:
\(\text{92}\) \(\text{cm}\) \(\div\) \(\text{50}\) = \(\text{1,84}\) \(\text{cm}\)
\(\text{188}\) \(\text{cm}\) \(\div\) \(\text{50}\) = \(\text{3,76}\) \(\text{cm}\)
Bedside table real measurements:
\(\text{400}\) \(\text{mm}\)
\(\text{400}\) \(\text{mm}\) \(\div\) \(\text{50}\) = \(\text{8}\) \(\text{mm}\)
Scale drawing:

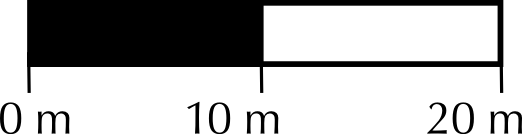
 You measure the distance on the map to be \(\text{15}\) \(\text{cm}\). What is the actual distance?
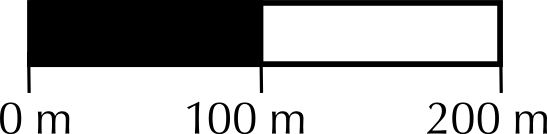
You measure the distance on the map to be \(\text{15}\) \(\text{cm}\). What is the actual distance?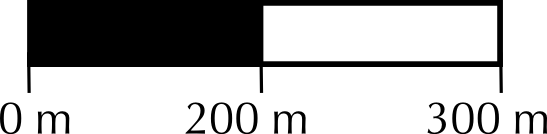 You measure the distance between two points on the map to be \(\text{11}\) \(\text{cm}\). What is the distance on the ground?
You measure the distance between two points on the map to be \(\text{11}\) \(\text{cm}\). What is the distance on the ground?