Where does the number \(-\frac{12}{3}\) belong in the diagram?
First simplify the fraction: \(-\frac{12}{3} = -4\)
\(-\text{4}\) is an integer, so it falls into the set \(\mathbb{Z}\).
|
Previous
1.2 The real number system
|
Next
1.4 Rounding off
|
A rational number (\(\mathbb{Q}\)) is any number which can be written as:
\[\frac{a}{b}\]where \(a\) and \(b\) are integers and \(b \ne 0\).
The following numbers are all rational numbers:
\[\frac{10}{1} \; ; \; \frac{21}{7} \; ; \; \frac{-1}{-3} \; ; \; \frac{10}{20} \; ; \; \frac{-3}{6}\]We see that all numerators and all denominators are integers.
This means that all integers are rational numbers, because they can be written with a denominator of \(\text{1}\).
Irrational numbers (\(\mathbb{Q}'\)) are numbers that cannot be written as a fraction with the numerator and denominator as integers.
Examples of irrational numbers:
\[\sqrt{2} \; ; \; \sqrt{3} \; ; \; \sqrt[3]{4} \; ; \; \pi \; ; \; \frac{1 + \sqrt{5}}{2}\]These are not rational numbers, because either the numerator or the denominator is not an integer.
All integers and fractions with integer numerators and non-zero integer denominators are rational numbers. Remember that when the denominator of a fraction is zero then the fraction is undefined.
You can write any rational number as a decimal number but not all decimal numbers are rational numbers. These types of decimal numbers are rational numbers:
Decimal numbers that end (or terminate). For example, the fraction \(\frac{4}{10}\) can be written as \(\text{0,4}\).
Decimal numbers that have a repeating single digit. For example, the fraction \(\frac{1}{3}\) can be written as \(\text{0,}\dot{3}\) or \(\text{0,}\overline{3}\). The dot and bar notations are equivalent and both represent recurring \(\text{3}\)'s, i.e. \(\text{0,}\dot{3} = \text{0,}\overline{3} = \text{0,333...}\).
Decimal numbers that have a recurring pattern of multiple digits. For example, the fraction \(\frac{2}{11}\) can also be written as \(\text{0,}\overline{18}\). The bar represents a recurring pattern of \(\text{1}\)'s and \(\text{8}\)'s, i.e. \(\text{0,}\overline{18} = \text{0,181818...}\).
You may see a full stop instead of a comma used to indicate a decimal number. So the number \(\text{0,4}\) can also be written as 0.4
Notation: You can use a dot or a bar over the repeated digits to indicate that the decimal is a recurring decimal. If the bar covers more than one digit, then all numbers beneath the bar are recurring.
If you are asked to identify whether a number is rational or irrational, first write the number in decimal form. If the number terminates then it is rational. If it goes on forever, then look for a repeated pattern of digits. If there is no repeated pattern, then the number is irrational.
When you write irrational numbers in decimal form, you may continue writing them for many, many decimal places. However, this is not convenient and it is often necessary to round off.
Rounding off an irrational number makes the number a rational number that approximates the irrational number.
Which of the following are not rational numbers?
\(\pi =\text{3,14159265358979323846264338327950288419716939937510...}\)
\(\text{1,4}\)
\(\text{1,618033989...}\)
\(\text{100}\)
\(\text{1,7373737373...}\)
\(\text{0,}\overline{02}\)
Irrational, decimal does not terminate and has no repeated pattern.
Rational, decimal terminates.
Irrational, decimal does not terminate and has no repeated pattern.
Rational, all integers are rational.
Rational, decimal has repeated pattern.
Rational, decimal has repeated pattern.
A decimal number has an integer part and a fractional part. For example, \(\text{10,589}\) has an integer part of \(\text{10}\) and a fractional part of \(\text{0,589}\) because \(10 + \text{0,589} = \text{10,589}\).
Each digit after the decimal point is a fraction with a denominator in increasing powers of \(\text{10}\).
For example:
\(\text{0,1}\) is \(\frac{1}{\text{10}}\)
\(\text{0,01}\) is \(\frac{1}{\text{100}}\)
\(\text{0,001}\) is \(\frac{1}{\text{1 000}}\)
This means that
\begin{align*} \text{10,589} & = 10 + \frac{5}{10} + \frac{8}{100} + \frac{9}{\text{1 000}}\\ & = \frac{\text{10 000}}{\text{1 000}} + \frac{\text{500}}{\text{1 000}} + \frac{80}{\text{1 000}} + \frac{9}{\text{1 000}}\\ & = \frac{\text{10 589}}{\text{1 000}} \end{align*}The following two videos explain how to convert decimals into rational numbers.
Part 1
Part 2
When the decimal is a recurring decimal, a bit more work is needed to write the fractional part of the decimal number as a fraction.
Write \(\text{0,}\dot{3}\) in the form \(\frac{a}{b}\) (where \(a\) and \(b\) are integers).
Write \(\text{5,}\dot{4}\dot{3}\dot{2}\) as a rational fraction.
In the first example, the decimal was multiplied by \(\text{10}\) and in the second example, the decimal was multiplied by \(\text{1 000}\). This is because there was only one digit recurring (i.e. \(\text{3}\)) in the first example, while there were three digits recurring (i.e. \(\text{432}\)) in the second example.
In general, if you have one digit recurring, then multiply by \(\text{10}\). If you have two digits recurring, then multiply by \(\text{100}\). If you have three digits recurring, then multiply by \(\text{1 000}\) and so on.
Not all decimal numbers can be written as rational numbers. Why? Irrational decimal numbers like \(\sqrt{2}=\text{1,4142135...}\) cannot be written with an integer numerator and denominator, because they do not have a pattern of recurring digits and they do not terminate.
The figure here shows the Venn diagram for the special sets \(\mathbb{N}, \mathbb{N}_0\) and \(\mathbb{Z}\).
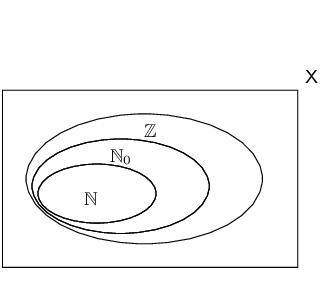
Where does the number \(-\frac{12}{3}\) belong in the diagram?
First simplify the fraction: \(-\frac{12}{3} = -4\)
\(-\text{4}\) is an integer, so it falls into the set \(\mathbb{Z}\).
In the following list, there are two false statements and one true statement. Which of the statements is true?
Consider each option carefully:
So only (ii) is true.
The figure here shows the Venn diagram for the special sets \(\mathbb{N}, \mathbb{N}_0\) and \(\mathbb{Z}\).

Where does the number \(- \frac{1}{2}\) belong in the diagram?
\(- \frac{1}{2}\) is in its simplest form, therefore it is not in \(\mathbb{N}\), \(\mathbb{N}_0\) or \(\mathbb{Z}\). It is in the space between the rectangle and \(\mathbb{Z}\).
In the following list, there are two false statements and one true statement. Which of the statements is true?
Consider each option carefully:
So only (ii) is true.
State whether the following numbers are real, non-real or undefined.
\(-\sqrt{3}\) has no minus sign under the square root (the minus is outside the root) and is not divided by zero, so it is real.
\(\dfrac{0}{\sqrt{2}}\) has no minus sign under the square root (the minus is outside the root) and is not divided by zero, so it is real.
\(\sqrt{-9}\) has a minus sign under the square root so it is non-real.
\(\dfrac{-\sqrt{7}}{0}\) has division by zero so it is undefined.
\(-\sqrt{-16}\) has a negative number under the square root so it is non-real.
\(\sqrt{2}\) has no minus under the square root (the minus is outside the root), is not divided by zero, so it is real.
State whether the following numbers are rational or irrational. If the number is rational, state whether it is a natural number, whole number or an integer.
\(-\frac{1}{3}\)
\(-\frac{1}{3}\) is rational. A fraction of integers is a rational number.
\(\text{0,651268962154862...}\)
\(\text{0,651268962154862...}\) is irrational. It cannot be simplified to a fraction of integers.
\(\dfrac{\sqrt{9}}{3}\) is rational, an integer, a whole number and a natural number. An integer is a rational number.
\(\pi^{2}\) is irrational. It cannot be simplified to a fraction of integers.
\(\pi^4\)
\(\pi^4\) is irrational. It cannot be simplified to a fraction of integers.
\(\sqrt[3]{19}\)
\(\sqrt[3]{19}\) is irrational. It cannot be simplified to a fraction of integers.
\(\left( \sqrt[3]{1} \right)^7\)
\(\left( \sqrt[3]{1} \right)^7\) is rational, an integer, a whole number and a natural number. It can be written as an integer.
\(\pi\) is irrational. \(\text{3}\) is rational (it is an integer). Any rational number added to any irrational number is irrational.
Therefore \(\pi + 3\) is irrational.
\(\pi\) is irrational. \(\text{0,858408346}\) is rational (it is a terminating decimal). Any rational number added to any irrational number is irrational.
Therefore \(\pi + \text{0,858408346}\) is irrational.
If \(a\) is an integer, \(b\) is an integer and \(c\) is irrational, which of the following are rational numbers?
\(\dfrac{5}{6}\)
\(\frac{5}{6}\) is rational.
\(\dfrac{a}{3}\)
Since \(a\) is an integer, \(\frac{a}{3}\) is rational.
\(\dfrac{-2}{b}\)
Since \(b\) is an integer, \(\frac{-2}{b}\) is rational.
Note that \(b\) cannot be \(\text{0}\) as that makes the fraction undefined.
\(\dfrac{1}{c}\)
Since \(c\) is irrational, \(\frac{1}{c}\) is irrational.
For each of the following values of \(a\) state whether \(\frac{a}{14}\) is rational or irrational.
\(\text{1}\)
\(\frac{a}{14} = \frac{1}{14}\) is rational.
\(-\text{10}\)
\(\frac{a}{14} = \frac{-10}{14}\) is rational.
\(\sqrt{2}\)
\(\frac{a}{14} = \frac{\sqrt{2}}{14}\) is irrational.
\(\text{2,1}\)
\(\frac{a}{14} = \frac{\text{2,1}}{14}\) is rational.
Consider the following list of numbers:
\[-3 \; ; \; 0 \; ; \; \sqrt{-1} \; ; \; -8\frac{4}{5} \; ; \; -\sqrt{8} \; ; \; \frac{22}{7} \; ; \; \frac{14}{0} \; ; \; 7 \; ; \; \text{1,}\overline{34} \; ; \; \text{3,3231089...} \; ; \; 3+\sqrt{2} \; ; \; 9\frac{7}{10} \; ; \; \pi \; ; \; 11\]Which of the numbers are:
natural numbers
Check which of the numbers are in the set \(\left\{1; 2; 3; 4;\ldots\right\}\). Therefore \(\text{7}\) and \(\text{11}\) are natural numbers.
irrational numbers
Remember that rational numbers can be written as \(\frac{a}{b}\) where \(a\) and \(b\) are integers. Also remember that rational numbers include terminating decimal numbers. Therefore \(-\sqrt{8} \; ; \; \text{3,3231089...} \; ; \; 3+\sqrt{2} \; ; \; \pi\) are all irrational.
non-real numbers
Any number that is a square root of a negative number is non-real. Therefore only \(\sqrt{-1}\) is non-real.
rational numbers
Remember that rational numbers can be written as \(\frac{a}{b}\) where \(a\) and \(b\) are integers. Also remember that rational numbers include terminating decimal numbers. Therefore \(-3 \; ; \; 0 \; ; \; -8\frac{4}{5} \; ; \; \frac{22}{7} \; ; \; 7 \; ; \; \text{1,}\overline{34} \; ; \; 9\frac{7}{10} \; ; \; 11\) are all rational numbers.
integers
Check which of the numbers are in the set \(\left\{\ldots; -3; -2; -1; 0; 1; 2; 3;\ldots\right\}\). Therefore \(-3 \; ; \; 7 \; ; \; 11\) are integers.
undefined
Any fraction divided by \(\text{0}\) is undefined. Therefore only \(\frac{14}{0}\) is undefined.
For each of the following numbers:
write the next three digits and
state whether the number is rational or irrational.
Rational, there is a repeating pattern of digits.
The number does not terminate (this is shown by the \(\ldots\)). There is also no indication of a repeating pattern of digits since there is not dot or bar over any of the numbers. The next three digits could be any numbers.
Note that while it looks like there is a pattern in the digits we do not know if this pattern continues on.
Irrational, there is no repeating pattern.
The number does not terminate (this is shown by the \(\ldots\)). There is also no indication of a repeating pattern of digits since there is not dot or bar over any of the numbers. The next three digits could be any numbers.
Note that while it looks like there is a pattern in the digits we do not know if this pattern continues on.
Irrational, there is no repeating pattern.
The number does not terminate (this is shown by the \(\ldots\)). There is also no indication of a repeating pattern of digits since there is not dot or bar over any of the numbers. The next three digits could be any numbers.
Note that while it looks like there is a pattern in the digits we do not know if this pattern continues on.
Irrational, there is no repeating pattern.
Rational, there is a repeating pattern.
Write the following as fractions:
\(\text{0,1}\)
\(\text{0,1}=\frac{1}{10}\)
\(\text{0,12}\)
\(\text{0,58}\)
\(\text{0,2589}\)
Write the following using the recurring decimal notation:
\(\text{0,1111111...}\)
We see that only the digit \(\text{1}\) is repeated and so we can write this as: \(\text{0,}\dot{1}\).
\(\text{0,1212121212...}\)
There is a repeating pattern of \(\text{12}\) and so we can write this number as: \(\text{0,}\overline{12}\)
\(\text{0,123123123123...}\)
There is a repeating pattern of \(\text{123}\) and so we can write this number as: \(\text{0,}\overline{123}\)
\(\text{0,11414541454145...}\)
The pattern 4145 repeats and so we can write this number as: \(\text{0,11}\overline{4145}\).
Write the following in decimal form, using the recurring decimal notation:
\(\dfrac{2}{3}\)
\(1\dfrac{3}{11}\)
\(4\dfrac{5}{6}\)
\(2\dfrac{1}{9}\)
Write the following decimals in fractional form:
\(\text{0,}\dot{5}\)
\(\text{0,6}\dot{3}\)
\(\text{5,}\overline{31}\)
|
Previous
1.2 The real number system
|
Table of Contents |
Next
1.4 Rounding off
|