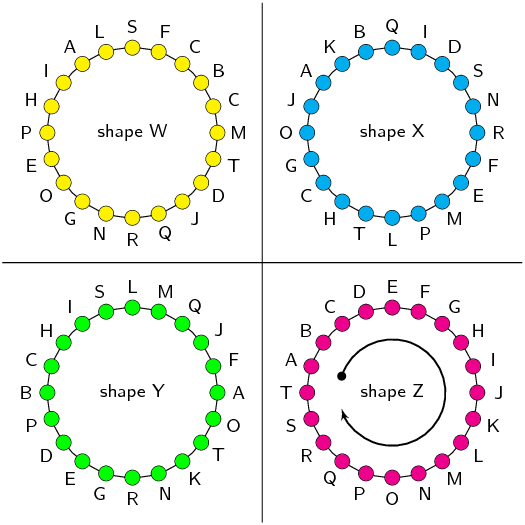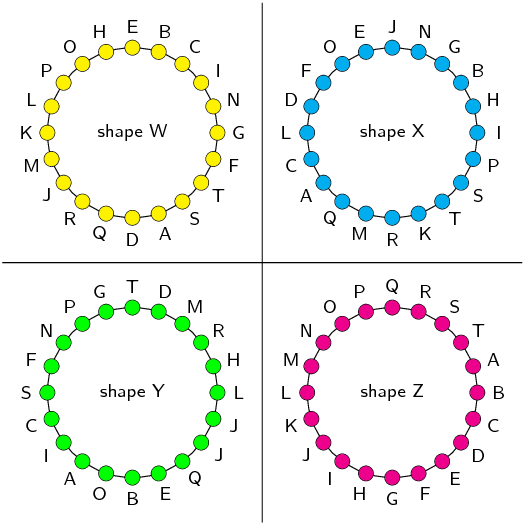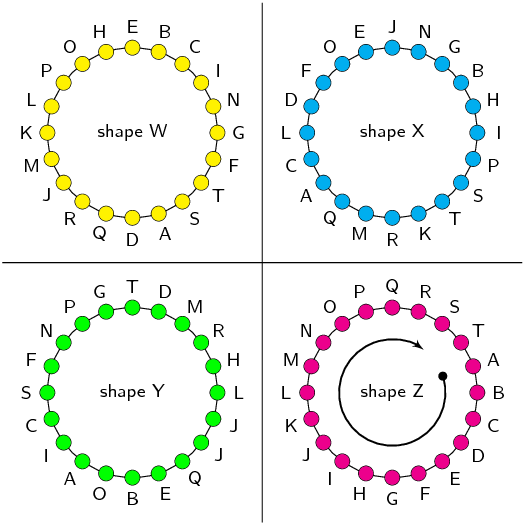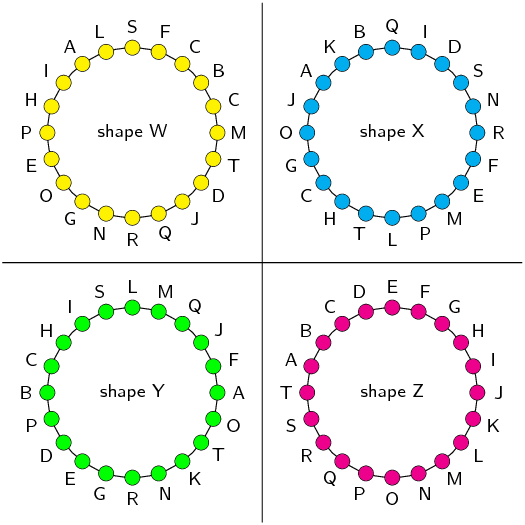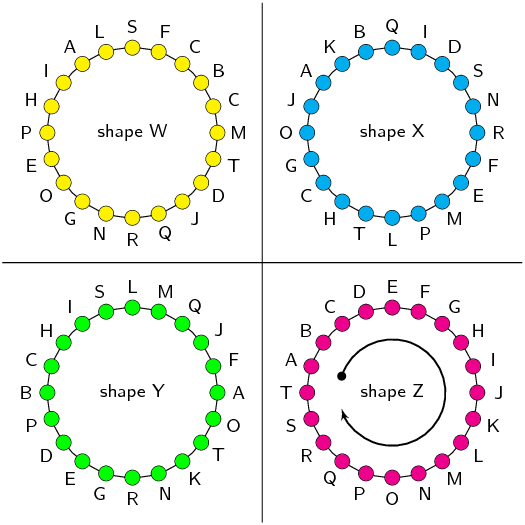You are given the following diagram, with various points shown:

Find the coordinates of point \(D\).
For this question, we are only interested in point \(D\). From the graph we can read off the \(x\) and
\(y\) values.
Point \(D\) has the following coordinates: \((3;3)\).
You are given the following diagram, with various points shown:

Find the coordinates of all the labelled points.
From the graph we can read off the \(x\) and \(y\) values for each point.
\(A(3;-4)\), \(B(3;-3)\), \(C(-3;-4)\), \(D(5;-3)\) and \(E(5;-4)\).
You are given the following diagram, with various points shown:

Which point lies at the coordinates \((5;-4)\)?
For this question, we are must find point \((5;-4)\).
On the graph we can trace the \(x\) and \(y\) values to find which point lies at the coordinates
\((5;-4)\).
Doing so we find that point \(E\) lies at the coordinates \((5;-4)\).
You are given the following diagram, with various points shown:

Which point lies at the coordinates \((-4;-3)\)?
For this question, we are must find point \((-4;-3)\).
On the graph we can trace the \(x\) and \(y\) values to find which point lies at the coordinates
\((-4;-3)\).
Doing so we find that point \(B\) lies at the coordinates \((-4;-3)\).
You are given the following diagram, with 4 shapes drawn.
All the shapes are identical, but each shape uses a different naming convention:
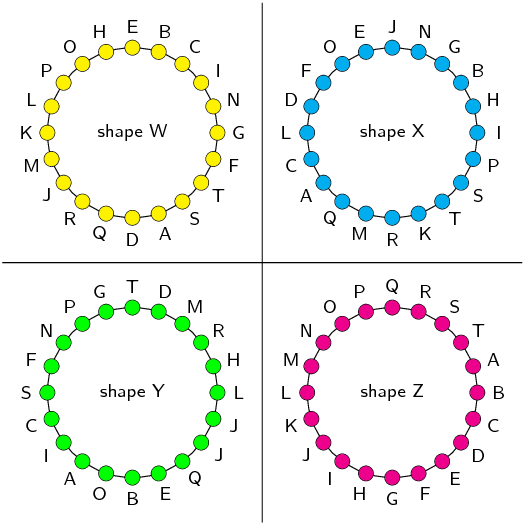
Which shape uses the correct naming convention?
We recall that the correct naming convention for a shape is in alphabetical order,
either clockwise or anti-clockwise around the shape.
From the diagram, we can see that only shape Z sticks to this naming convention.
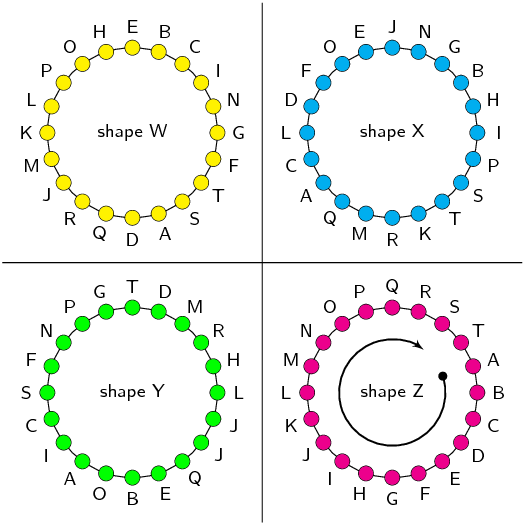
You are given the following diagram, with 4 shapes drawn.
All the shapes are identical, but each shape uses a different naming convention:
Which shape uses the correct naming convention?
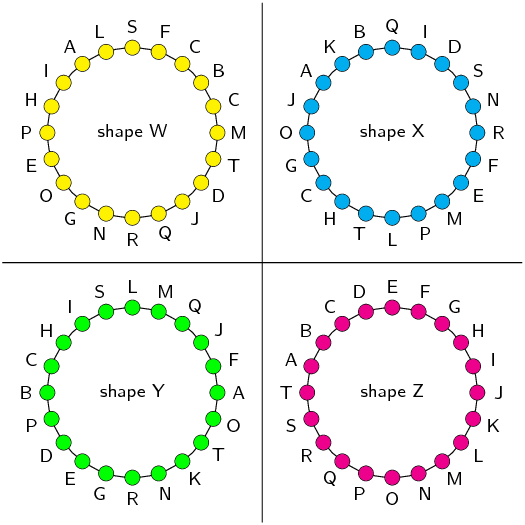
We recall that the correct naming convention for a shape is in alphabetical order,
either clockwise or anti-clockwise around the shape.
From the diagram, we can see that only shape Z sticks to this naming convention.