Look at the graph below

Solve the equations \(y = 2x + 1\) and \(y = -x - 5\) simultaneously
From the graph we can see that the lines intersect at \(x = -2\) and \(y = -3\)
|
Previous
4.3 Solving quadratic equations
|
Next
4.5 Word problems
|
Up to now we have solved equations with only one unknown variable. When solving for two unknown variables, two equations are required and these equations are known as simultaneous equations. The solutions are the values of the unknown variables which satisfy both equations simultaneously. In general, if there are \(n\) unknown variables, then \(n\) independent equations are required to obtain a value for each of the \(n\) variables.
An example of a system of simultaneous equations is:
\begin{align*} x + y & = -1 \\ 3 & = y - 2x \end{align*}We have two independent equations to solve for two unknown variables. We can solve simultaneous equations algebraically using substitution and elimination methods. We will also show that a system of simultaneous equations can be solved graphically.
Use the simplest of the two given equations to express one of the variables in terms of the other.
Substitute into the second equation. By doing this we reduce the number of equations and the number of variables by one.
We now have one equation with one unknown variable which can be solved.
Use the solution to substitute back into the first equation to find the value of the other unknown variable.
The following video shows how to solve simultaneous equations using substitution.
Solve for \(x\) and \(y\):
\begin{align*} x - y & =1 \qquad \ldots\left(1\right) \\ 3 & = y - 2x \qquad \ldots\left(2\right) \end{align*}Solve the following system of equations:
\begin{align*} 4y + 3x & = 100 \qquad \ldots\left(1\right) \\ 4y - 19x & = 12 \qquad \ldots \left(2\right) \end{align*}Solve the following system of equations:
\begin{align*} 3x + y & = 2 \qquad \ldots \left(1\right) \\ 6x - y & = 25 \quad \ldots \left(2\right) \end{align*}The coefficients of \(y\) in the given equations are \(\text{1}\) and \(-\text{1}\). Eliminate the variable \(y\) by adding equation \(\left(1\right)\) and equation \(\left(2\right)\) together:
\[\begin{array}{cccc} & 3x + y & = & 2 \\ + & 6x - y & = & 25 \\ \hline & 9x + 0 & = & 27 \end{array}\]Solve the following system of equations:
\begin{align*} 2a - 3b & = 5 \qquad \ldots \left(1\right) \\ 3a - 2b & = 20 \qquad \ldots\left(2\right) \end{align*}By multiplying equation \(\left(1\right)\) by \(\text{3}\) and equation \(\left(2\right)\) by \(\text{2}\), both coefficients of \(a\) will be \(\text{6}\).
\[\begin{array}{cccc} & 6a - 9b & = & 15 \\ - & (6a - 4b & = & 40) \\ \hline & 0 - 5b & = & -25 \end{array}\](When subtracting two equations, be careful of the signs.)
This section can be included in the chapter on functions and graphs with graphs of linear equations. Before beginning this section it may be necessary to revise plotting graphs of linear equations with your learners.
It is also important that learners are either given the graphs or are encouraged to draw accurate graphs on graph paper to help them solve simultaneous equations graphically. Graph sketching software can be used in this section to ensure that graphs are accurate.
Simultaneous equations can also be solved graphically. If the graphs of each linear equation are drawn, then the solution to the system of simultaneous equations is the coordinates of the point at which the two graphs intersect.
For example:
\begin{align*} x & = 2y \qquad \ldots \left(1\right) \\ y & = 2x - 3 \qquad \ldots \left(2\right) \end{align*}The graphs of the two equations are shown below.

The intersection of the two graphs is \((2;1)\). So the solution to the system of simultaneous equations is \(x=2\) and \(y=1\). We can also check the solution using algebraic methods.
Substitute equation \((1)\) into \((2)\):
\begin{align*} x & = 2y \\ \therefore y & = 2(2y) - 3 \end{align*}Then solve for \(y\):
\begin{align*} y - 4y & = -3 \\ -3y & = -3 \\ \therefore y & = 1 \end{align*}Substitute the value of \(y\) back into equation \((1)\):
\begin{align*} x & = 2(1) \\ \therefore x & = 2 \end{align*}Notice that both methods give the same solution.
You can use an online tool such as graphsketch to draw the graphs and check your solution.
Solve the following system of simultaneous equations graphically:
\begin{align*} 4y + 3x & = 100 \qquad \ldots \left(1\right) \\ 4y - 19x & = 12 \qquad \ldots \left(2\right) \end{align*}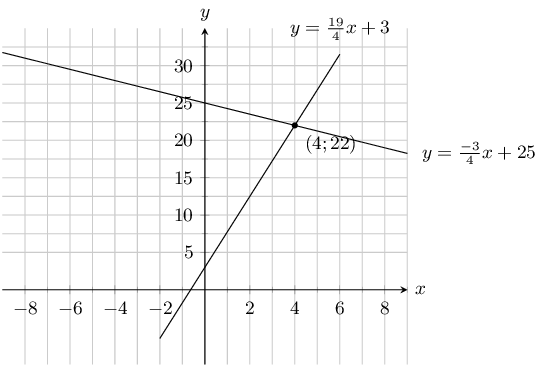
The two graphs intersect at \(\left(4;22\right)\)
Look at the graph below

Solve the equations \(y = 2x + 1\) and \(y = -x - 5\) simultaneously
From the graph we can see that the lines intersect at \(x = -2\) and \(y = -3\)
Look at the graph below

Solve the equations \(y = 2x - 1\) and \(y = 2x + 1\) simultaneously
The lines are parallel. Therefore there is no solution to \(x\) and \(y\).
Look at the graph below

Solve the equations \(y = -2x + 1\) and \(y = -x - 1\) simultaneously
From the graph we can see that the lines intersect at \(x = 2\) and \(y = -3\)
Solve for \(x\) and \(y\):
\(- 10 x = -1\) and \(- 4 x + 10 y = -9\).
Solve for \(x\):
\begin{align*} - 10x = -1\\ \therefore x = \frac{1}{10} \end{align*}Substitute the value of \(x\) into the second equation and solve for \(y\):
\begin{align*} -4x + 10y & = -9 \\ -4\left(\frac{1}{10}\right) + 10y & = -9 \\ \frac{-4}{10} + 10y & = -9 \\ 100y & = -90 + 4 \\ y & = \frac{-86}{100} \\ & = \frac{-43}{50} \end{align*}Therefore \(x = \frac{1}{10} \text{ and } y = - \frac{43}{50}\).
\(3x - 14y = 0\) and \(x - 4y + 1 = 0\)
Write \(x\) in terms of \(y\):
\begin{align*} 3x - 14y & = 0 \\ 3x & = 14y \\ x & = \frac{14}{3}y \end{align*}Substitute value of \(x\) into second equation:
\begin{align*} x - 4y + 1 & = 0 \\ \frac{14}{3}y - 4y + 1 & = 0 \\ 14y - 12y + 3 & = 0 \\ 2y & = -3 \\ y & = -\frac{3}{2} \end{align*}Substitute value of \(y\) back into first equation:
\begin{align*} x & = \frac{14\left(-\frac{3}{2}\right)}{3} \\ & = -7 \end{align*}Therefore \(x = -7 \text{ and } y = -\frac{3}{2}\).
\(x + y = 8\) and \(3x + 2y = 21\)
Write \(x\) in terms of \(y\):
\begin{align*} x + y & = 8 \\ x & = 8 - y \end{align*}Substitute value of \(x\) into second equation:
\begin{align*} 3x + 2y & = 21 \\ 3(8 - y) + 2y & = 21 \\ 24 - 3y + 2y & = 21 \\ y & = 3 \end{align*}Substitute value of \(y\) back into first equation:
\[x = 5\]Therefore \(x = 5 \text{ and } y = 3\).
\(y = 2x + 1\) and \(x + 2y + 3 = 0\)
Write \(y\) in terms of \(x\):
\[y = 2x + 1\]Substitute value of \(y\) into second equation:
\begin{align*} x + 2y + 3 & = 0 \\ x + 2(2x + 1) + 3 & = 0 \\ x + 4x + 2 + 3 & = 0 \\ 5x & = -5 \\ x & = -1 \end{align*}Substitute value of \(x\) back into first equation:
\begin{align*} y & = 2(-1) + 1 \\ & = -1 \end{align*}Therefore \(x = -1 \text{ and } y = -1\).
\(5x-4y = 69\) and \(2x+3y = 23\)
Make \(x\) the subject of the first equation:
\begin{align*} 5x-4y &= 69 \\ 5x &= 69+4y \\ x &= \frac{69+4y}{5} \end{align*}Substitute value of \(x\) into second equation:
\begin{align*} 2x+3y &= 23 \\ 2 \left(\frac{69+4y}{5} \right) +3y &= 23 \\ 2(69+4y) +3(5)y &= 23(5) \\ 138+8y+15y &= 115\\ 23y &= -23 \\ \therefore y &= -1 \end{align*}Substitute value of \(y\) back into first equation:
\begin{align*} x &= \frac{69+4y}{5} \\ &= \frac{69+4(-1)}{5} \\ &= 13 \end{align*}Therefore \(x =13 \text{ and } y = -1\).
\(x + 3y = 26\) and \(5x + 4y = 75\)
Make \(x\) the subject of the first equation:
\begin{align*} x + 3y &= 26 \\ x &= 26 - 3y \end{align*}Substitute value of \(x\) into second equation:
\begin{align*} 5x+4y &= 75 \\ 5(26 - 3y) + 4y &= 75 \\ 130 - 15y + 4y &= 75 \\ -11y &= -55 \\ \therefore y &= 5 \end{align*}Substitute value of \(y\) back into first equation:
\begin{align*} x &= 26 - 3y \\ &= 26 - 3(5) \\ &= 11 \end{align*}Therefore \(x =11 \text{ and } y = 5\).
\(3x - 4y = 19\) and \(2x - 8y = 2\)
If we multiply the first equation by 2 then the coefficient of \(y\) will be the same in both equations:
\begin{align*} 3x - 4y &= 19 \\ 3(2)x - 4(2)y & = 19(2) \\ 6x - 8y & = 38 \end{align*}Now we can subtract the second equation from the first:
\[\begin{array}{cccc} & 6x - 8y & = & 38 \\ - & (2x - 8y & = & 2) \\ \hline & 4x + 0 & = & 36 \end{array}\]Solve for \(x\):
\begin{align*} \therefore x &= \frac{36}{4} \\ & = 9 \end{align*}Substitute the value of \(x\) into the first equation and solve for \(y\):
\begin{align*} 3x-4y &= 19 \\ 3(9)-4y &= 19\\ \therefore y &= \frac{19-3(9)}{-4} \\ &= 2 \end{align*}Therefore \(x = 9 \text{ and } y = 2\).
\(\dfrac{a}{2} + b = 4\) and \(\dfrac{a}{4} - \dfrac{b}{4} = 1\)
Make \(a\) the subject of the first equation:
\begin{align*} \frac{a}{2} + b & = 4 \\ a + 2b & = 8 \\ a & = 8 - 2b \end{align*}Substitute value of \(a\) into second equation:
\begin{align*} \frac{a}{4} - \frac{b}{4} & = 1 \\ a - b & = 4 \\ 8 - 2b - b & = 4 \\ 3b & = 4 \\ b & = \frac{4}{3} \end{align*}Substitute value of \(b\) back into first equation:
\begin{align*} a & = 8 - 2\left(\frac{4}{3}\right) \\ & = \frac{16}{3} \end{align*}Therefore \(a = \frac{16}{3} \text{ and } b = \frac{4}{3}\).
\(-10x + y = -1\) and \(-10x - 2y = 5\)
If we subtract the second equation from the first then we can solve for \(y\):
\[\begin{array}{cccc} & -10x + y & = & -1 \\ - & (-10x - 2y & = & 5) \\ \hline & 0 + 3y & = & -6 \end{array}\]Solve for \(y\):
\begin{align*} 3y & = -6 \\ \therefore y &= -2 \end{align*}Substitute the value of \(y\) into the first equation and solve for \(x\):
\begin{align*} -10x + y &= -1 \\ -10x - 2 &= -1\\ -10x &= 1 \\ x &= \frac{1}{-10} \end{align*}Therefore \(x = \frac{-1}{10} \text{ and } y = -2\).
\(- 10 x - 10 y = -2\) and \(2 x + 3 y = 2\)
Make \(x\) the subject of the first equation:
\begin{align*} - 10 x - 10 y = -2\\ 5x + 5y & = 1 \\ 5x & = 1 - 5y \\ \therefore x = -y + \frac{1}{5} \end{align*}Substitute the value of \(x\) into the second equation and solve for \(y\):
\begin{align*} 2x + 3y & = 2 \\ 2\left(-y + \frac{1}{5}\right) + 3y & = 2 \\ -2y + \frac{2}{5} + 3y & = 2 \\ y & = \frac{8}{5} \end{align*}Substitute the value of \(y\) in the first equation:
\begin{align*} 5x + 5y & = 1 \\ 5x + 5\left(\frac{8}{5}\right) & = 1 \\ 5x + 8 & = 1 \\ 5x & = -7 \\ x &= \frac{-7}{5} \end{align*}Therefore \(x = - \frac{7}{5} \text{ and } y = \frac{8}{5}\).
\(\dfrac{1}{x} + \dfrac{1}{y} = 3\) and \(\dfrac{1}{x} - \dfrac{1}{y} = 11\)
Rearrange both equations by multiplying by \(xy\):
\begin{align*} \frac{1}{x} + \frac{1}{y} & = 3 \\ y + x & = 3xy \\\\ \frac{1}{x} - \frac{1}{y} & = 11 \\ y - x & = 11xy \end{align*}Add the two equations together:
\[\begin{array}{cccc} & y + x & = & 3xy \\ + & (y - x & = & 11xy) \\ \hline & 2y + 0 & = & 14xy \end{array}\]Solve for \(x\):
\begin{align*} 2y & = 14xy \\ y & = 7xy \\ 1 & = 7x \\ x & = \frac{1}{7} \end{align*}Substitute value of \(x\) back into first equation:
\begin{align*} y + \frac{1}{7} & = 3\left(\frac{1}{7}\right)y \\ 7y + 1 & = 3y \\ 4y & = -1 \\ y & = -\frac{1}{4} \end{align*}Therefore \(x = \frac{1}{7} \text{ and } y = -\frac{1}{4}\).
\(y = \dfrac{2(x^2 + 2) - 3}{x^2 + 2}\) and \(y = 2 - \dfrac{3}{x^2 + 2}\)
Let
\begin{align*} \frac{2(x^2 + 2) - 3}{x^2 + 2} &= 2 - \frac{3}{x^2 + 2} \\ 2x^2 + 4 - 3 &= 2(x^2 + 2) - 3 \\ 2x^2 + 1 &= 2x^2 + 1 \\ 0 &= 0 \end{align*}Since this is true for all \(x\) in the real numbers, \(x\) can be any real number.
Look at what happens to \(y\) when \(x\) is very small or very large:
The smallest \(x\) can be is 0. When \(x=0\), \(y=2-\frac{3}{2}=\frac{1}{2}\).
If \(x\) gets very large, then the fraction \(\dfrac{3}{x^{2}+2}\) becomes very small (think about what happens when you divide a small number by a very large number). Then \(y = 2 - 0 = 2\).
From this we can see that \(\frac{1}{2}\leq y \leq 2\).
Therefore \(x\) can be any real number, \(\frac{1}{2} \leq y < 2\).
\(3a + b=\dfrac{6}{2a}\) and \(3a^2 = 3 - ab\)
Note \(a \neq 0\)
Look at the first equation
\begin{align*} 3a + b&=\frac{6}{2a} \\ 6a^2 + 2ab&=6 \\ 6a^2 &= 6 - 2ab \\ 3a^2 &= 3 - ab \end{align*}Note that this is the same as the second equation
\(a\) and \(b\) can be any real number except for \(\text{0}\).
Solve graphically and check your answer algebraically:
\(y + 2x = 0\) and \(y - 2x - 4 = 0\)
First write the equations in standard form:
\begin{align*} y + 2x & = 0 \\ y & = -2x \\\\ y - 2x - 4 & = 0 \\ y & = 2x + 4 \end{align*}Draw the graph:
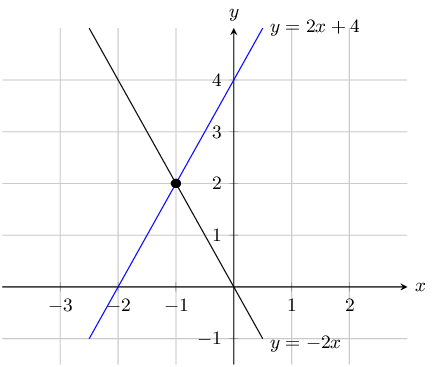
The graphs intersect at \((-1;2)\) so \(x = -1\) and \(y=2\).
Checking algebraically we get:
\[y = -2x\]Substitute value of \(y\) into second equation:
\begin{align*} y - 2x - 4 & = 0 \\ -2x - 2x - 4 & = 0 \\ -4x & = 4 \\ x & = -1 \end{align*}Substitute the value of \(x\) back into the first equation:
\begin{align*} y & = -2(-1) \\ y & = 2 \end{align*}\(x + 2y = 1\) and \(\dfrac{x}{3} + \dfrac{y}{2} = 1\)
First write the equations in standard form:
\begin{align*} x + 2y & = 1 \\ 2y & = -x + 1\\ y & = -\frac{1}{2}x + \frac{1}{2} \\ \\ \frac{x}{3} + \frac{y}{2} & = 1 \\ y & = -\frac{2}{3}{x} + 2 \end{align*}Draw the graph:
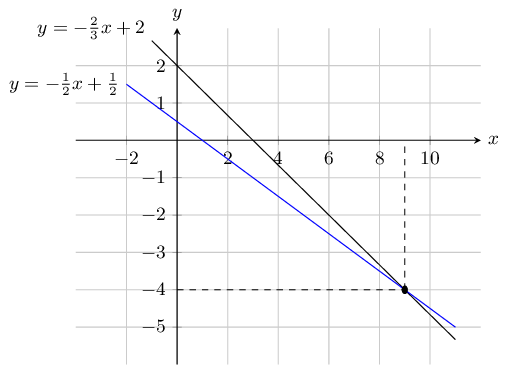
The graphs intersect at \((9;-4)\) so \(x = 9\) and \(y=-4\).
Checking algebraically we get:
\[x = -2y + 1\]Substitute value of \(x\) into first equation:
\begin{align*} \frac{-2y + 1}{3} + \frac{y}{2} & = 1 \\ -4y + 2 + 3y & = 6 \\ y & = -4 \end{align*}Substitute the value of \(y\) back into the first equation:
\begin{align*} x + 2(-4) & = 1 \\ x - 8 & = 1 \\ x & = 9 \end{align*}\(y - 2 = 6x\) and \(y - x = -3\)
First write the equations in standard form:
\begin{align*} y - 2 & = 6x \\ y & = 6x + 2\\\\ y - x & = -3 \\ y & = x - 3 \end{align*}Draw the graph:
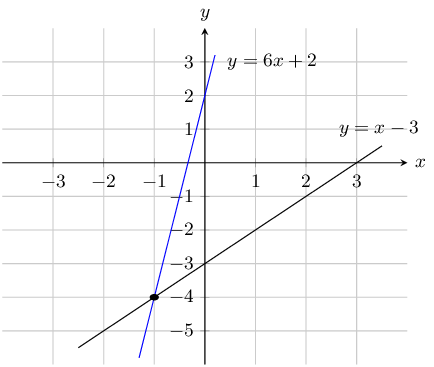
The graphs intersect at \((-1;-4)\) so \(x = -1\) and \(y=-4\).
Checking algebraically we get:
\[y = 6x + 2\]Substitute value of \(y\) into first equation:
\begin{align*} 6x + 2 & = x - 3 \\ 5x & = -5 \\ x & = -1 \end{align*}Substitute the value of \(x\) back into the first equation:
\begin{align*} y & = 6(-1) + 2 \\ y & = -4 \end{align*}\(2x + y = 5\) and \(3x - 2y = 4\)
First write the equations in standard form:
\begin{align*} 2x + y & = 5 \\ y & = -2x + 5\\ \\ 3x - 2y & = 4 \\ 2y & = 3x - 4 \\ y & = \frac{3}{2}x - 2 \end{align*}Draw the graph:
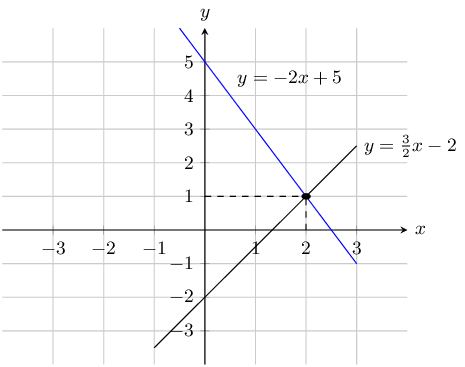
The graphs intersect at \((2;1)\) so \(x = 2\) and \(y=1\).
Checking algebraically we get:
\[y = -2x + 5\]Substitute value of \(y\) into first equation:
\begin{align*} -2x + 5 & = \frac{3}{2}x - 2 \\ -4x + 10 & = 3x - 4 \\ 7x & = 14 \\ x & = 2 \end{align*}Substitute the value of \(x\) back into the first equation:
\begin{align*} x & = -2(2) + 5 \\ y & = 1 \end{align*}\(5 = x + y\) and \(x = y - 2\)
First write the equations in standard form:
\begin{align*} 5 & = x + y \\ y & = -x + 5\\ \\ x & = y - 2 \\ y & = x + 2 \end{align*}Draw the graph:
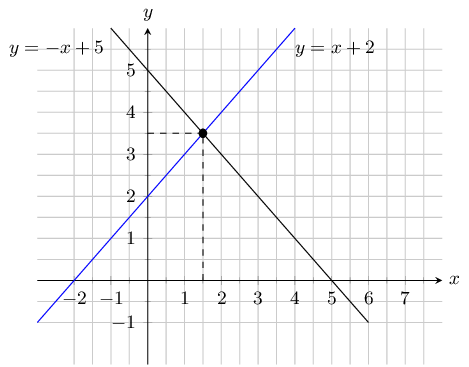
The graphs intersect at \((\text{1,5};\text{3,5})\) so \(x = \text{1,5}\) and \(y=\text{3,5}\).
Checking algebraically we get:
\[y = -x + 5\]Substitute value of \(y\) into second equation:
\begin{align*} x & = -x + 5 - 2 \\ 2x & = 3 \\ x & = \frac{3}{2} \end{align*}Substitute the value of \(x\) back into the first equation:
\begin{align*} 5 & = \frac{3}{2} + y \\ y & = \frac{7}{2} \end{align*}|
Previous
4.3 Solving quadratic equations
|
Table of Contents |
Next
4.5 Word problems
|