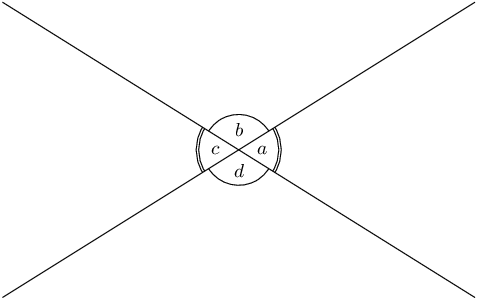
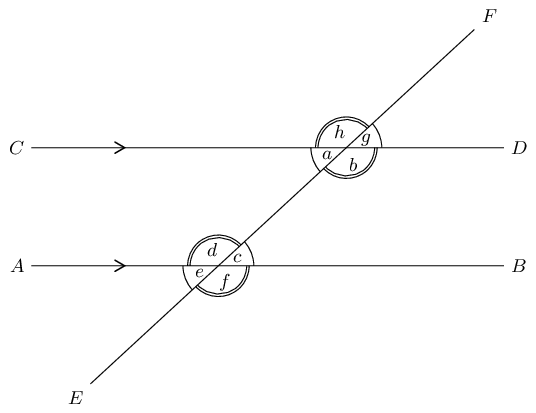
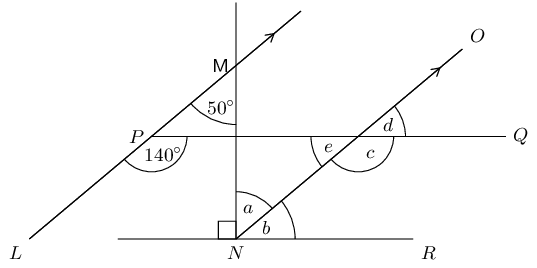
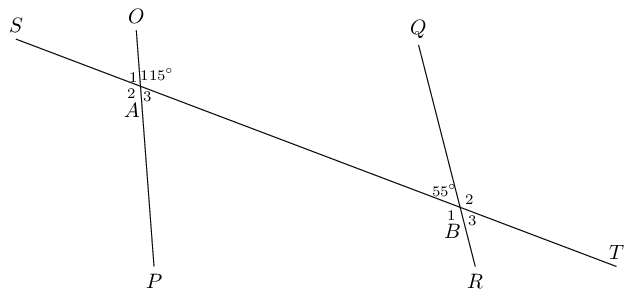
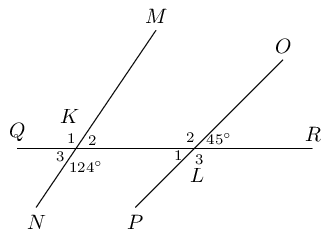
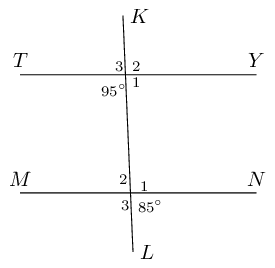
Use adjacent, corresponding, co-interior and alternate angles to fill in all the angles labelled with
letters in the diagram:
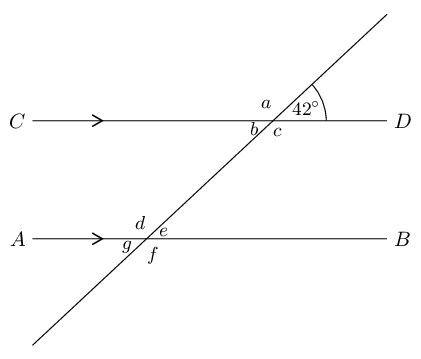
You can redraw the diagram and fill in the angles as you find them.
\[\begin{array}{rll}
a & = 180° - 42° = 138° & \text{(}\angle \text{s on a str line)} \\
b & = 42° & \text{(vert opp } \angle\text{s } = \text{)}\\
c & = 138° & \text{(vert opp } \angle\text{s } = \text{)}\\
d & = 138° & \text{(co-int }\angle\text{s; } AB \parallel CD \text{)}\\
e & = 180° - 138° = 42° & \text{(}\angle \text{s on a str line)}\\
f & = 138° & \text{(vert opp } \angle\text{s } =\text{)}\\
g & = 42° & \text{(vert opp } \angle\text{s } =\text{)}
\end{array}\]
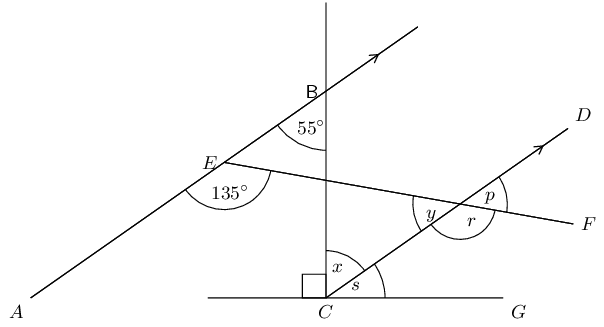
Find all the unknown angles in the figure:
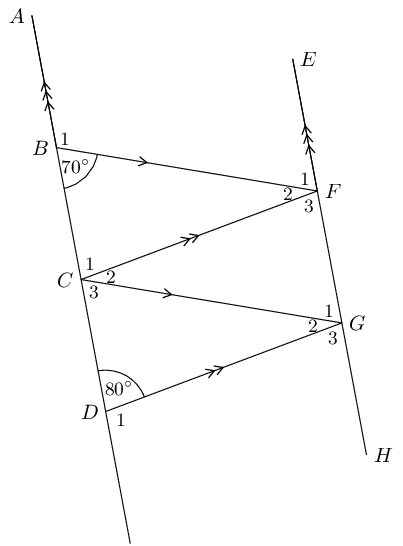
\[\begin{array}{rll}
\hat{B}_{1} & = 180° - 70° = 110° & \text{(}\angle \text{s on a str line)} \\
\hat{D}_{1} & = 180° - 80° = 100° & \text{(}\angle \text{s on a str line)} \\
\hat{F}_{1} & = 70° & \text{(co-int } \angle \text{s; } AD \parallel EH\text{)} \\
\hat{G}_{3} & = 80° & \text{(co-int } \angle \text{s; } AD \parallel EH\text{)} \\
\hat{C}_{3} & = 70° & \text{(corresp } \angle \text{s; } BF \parallel CG\text{)} \\
\hat{G}_{1} & = 70° & \text{(corresp } \angle \text{s; } BF \parallel CG\text{)} \\
\hat{G}_{2} & = 180° - 70° - 80° = 30° & \text{(}\angle \text{s on a str
line)} \\
\hat{C}_{2} & = 30° & \text{(alt } \angle \text{s; } CF \parallel DG\text{)} \\
\hat{F}_{2} & = 30° & \text{(alt } \angle \text{s; } BF \parallel CG\text{)} \\
\hat{F}_{3} & = 80° & \text{(}\angle \text{s on a str line)} \\
\hat{C}_{1} & = 80° & \text{(}\angle \text{s on a str line)}
\end{array}\]
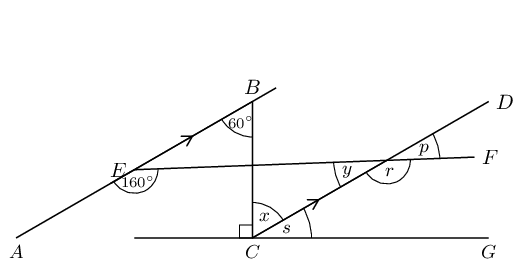
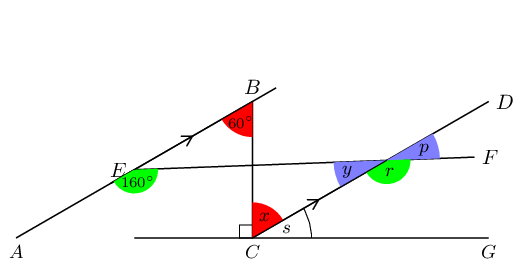
Find the value of \(x\) in the figure:
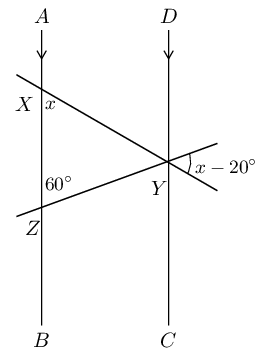
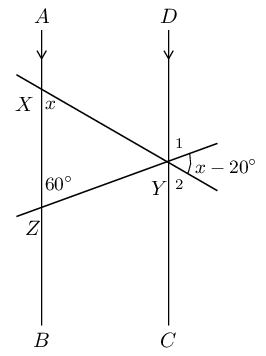
\(\hat{Y}_{1} = 60°\) (corresp \(\angle\)s; \(AB \parallel DC\)).
\(\hat{Y}_{2} = x\) (corresp \(\angle\)s; \(AB \parallel DC\)).
\begin{align*}
\therefore x + 60° + (x - 20°) &= 180° \qquad \text{(}\angle \text{s on a str line)}\\
2x &= 180° - 40° \\
2x &= 140° \\
\therefore x &= 70°
\end{align*}
If \(AB\) is parallel to \(CD\) and \(AB\) is parallel to \(EF\), explain why \(CD\) must be parallel
to \(EF\).

If \(a = 2\) and \(b = a\) then we know that \(b = 2\).
Similarly if \(AB \parallel CD\) and \(EF \parallel AB\) then we know that \(EF \parallel CD\).