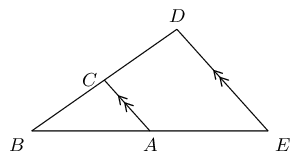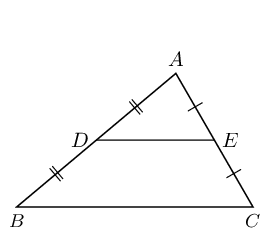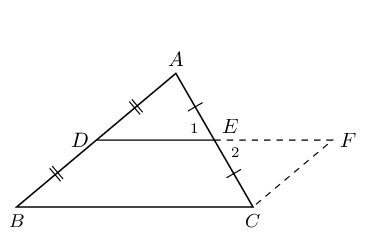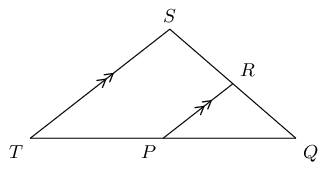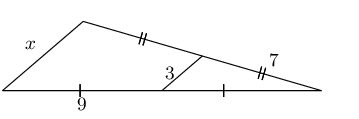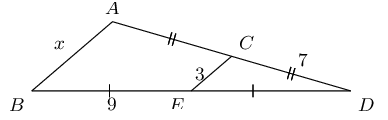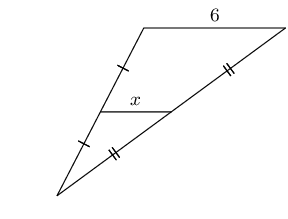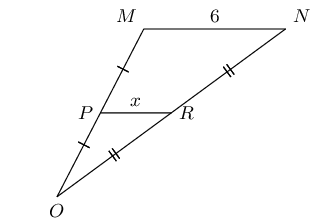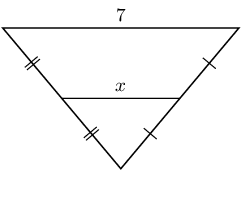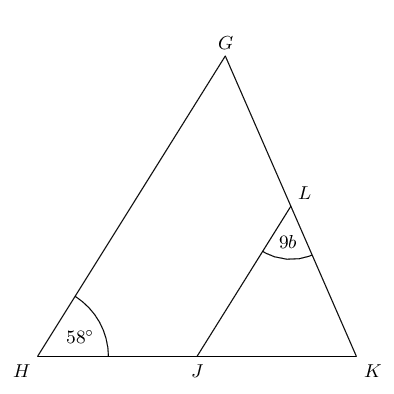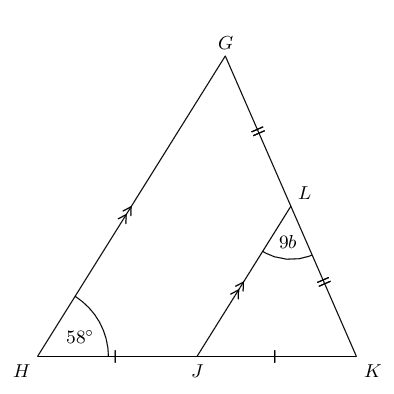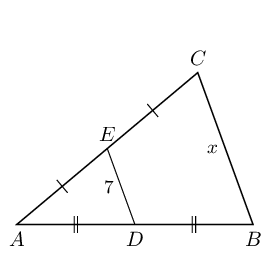
From the mid-point theorem we know:
\begin{align*}
BC & = 2 \times DE \\
x & = 2(7) \\
& = 14
\end{align*}
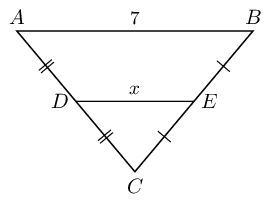
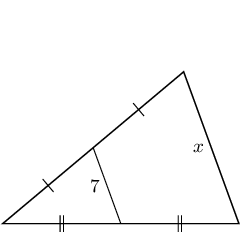
From the mid-point theorem we know:
\begin{align*}
AB & = 2 \times DE \\
7 & = 2x \\
\text{3,5} & = x
\end{align*}
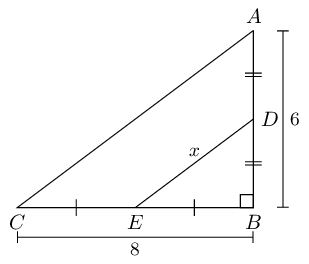
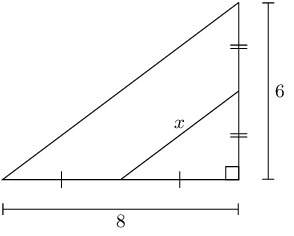
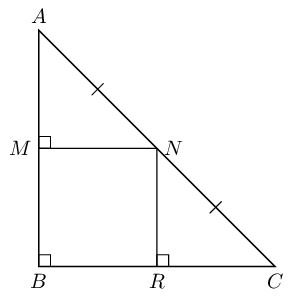
We can use the theorem of Pythagoras to find \(AC\):
\begin{align*}
AC^{2} & = BC^{2} + AB^{2} \\
& = (8)^{2} + (6)^{2} \\
& = 64 + 36 \\
& = 100 \\
AC & = 10
\end{align*}
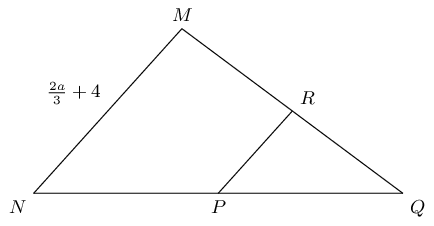
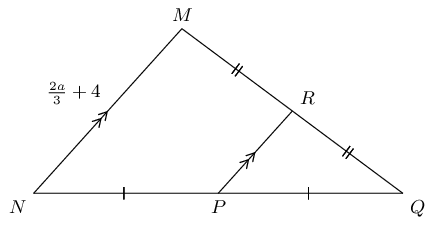
From the mid-point theorem we know:
\begin{align*}
AC & = 2 \times DE \\
10 & = 2x \\
\text{5} & = x
\end{align*}
From the mid-point theorem we know:
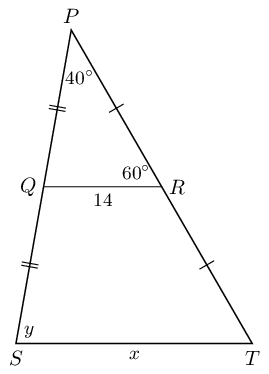
\begin{align*}
ST & = 2 \times QR \\
x & = 2(14) \\
& = 28
\end{align*}
To find \(y\) we note the following:
Therefore \(y = 100°\) (corresp \(\angle\)s; \(QR \parallel ST\)).
The final answer is: \(x = 28\text{ units}\) and \(y = 100°\).
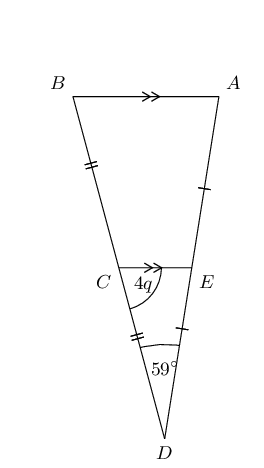
In the following diagram \(PQ = \text{2,5}\) and \(RT = \text{6,5}\).
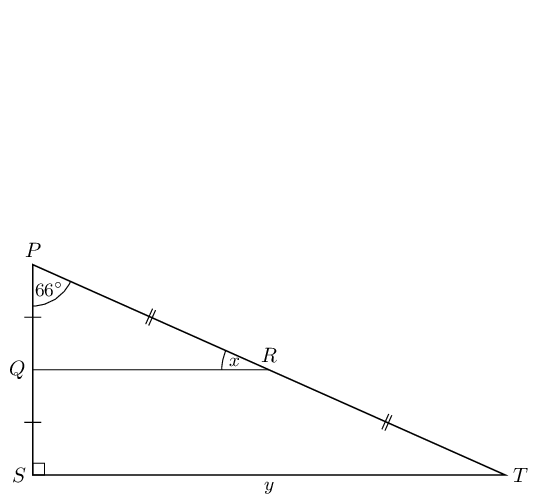
From the mid-point theorem we know that \(QR \parallel ST\). Therefore \(P\hat{Q}R = P\hat{S}T =
90°\) (corresp \(\angle\)s; \(QR \parallel ST\)).
Therefore \(x = 180° - 90° - 66° = 24°\) (sum of \(\angle\)s in \(\triangle\)).
To find \(y\) we note that \(PQ + QS = PS\) and \(PQ = QS\), therefore \(PS = 2PQ\). Similarly \(PT =
2RT\).
We can use the theorem of Pythagoras to find \(ST\):
\begin{align*}
ST^{2} & = PS^{2} + PT^{2} \\
& = 2PQ + 2RT \\
& = (2(\text{2,5}))^{2} + (2(\text{6,5}))^{2} \\
& = \text{25} + \text{169} \\
& = 194 \\
ST & = \text{13,93}
\end{align*}
Therefore: \(x = 24°\) and \(y = \text{13,93}\).