Calculate the \(y\)-intercept. Your answer must be correct to 2 decimal places.
The \(y\)-intercept is \((0;\text{0,33})\).
|
Previous
6.4 Hyperbolic functions
|
Next
6.6 Trigonometric functions
|
Functions of the general form \(y=a{b}^{x}+q\) are called exponential functions. In the equation \(a\) and \(q\) are constants and have different effects on the function.
Complete the following table for each of the functions and draw the graphs on the same system of axes: \(f(x)={2}^{x}\), \(g(x)={3}^{x}\), \(h(x)={5}^{x}\).
|
\(-\text{2}\) |
\(-\text{1}\) |
\(\text{0}\) |
\(\text{1}\) |
\(\text{2}\) |
|
|
\(f(x)={2}^{x}\) |
|||||
|
\(g(x)={3}^{x}\) |
|||||
|
\(h(x)={5}^{x}\) |
At what point do these graphs intersect?
Explain why they do not cut the \(x\)-axis.
Give the domain and range of \(h(x)\).
As \(x\) increases, does \(h(x)\) increase or decrease?
Which of these graphs increases at the slowest rate?
For \(y={k}^{x}\) and \(k>1\), the greater the value of \(k\), the steeper the curve of the graph. True or false?
Complete the following table for each of the functions and draw the graphs on the same system of axes: \(F(x)={\left(\dfrac{1}{2}\right)}^{x}\), \(G(x)={\left(\dfrac{1}{3}\right)}^{x}\), \(H(x)={\left(\dfrac{1}{5}\right)}^{x}\)
|
\(-\text{2}\) |
\(-\text{1}\) |
\(\text{0}\) |
\(\text{1}\) |
\(\text{2}\) |
|
|
\(F(x)={\left(\frac{1}{2}\right)}^{x}\) |
|||||
|
\(G(x)={\left(\frac{1}{3}\right)}^{x}\) |
|||||
|
\(H(x)={\left(\frac{1}{5}\right)}^{x}\) |
Give the \(y\)-intercept for each function.
Describe the relationship between the graphs \(f(x)\) and \(F(x)\).
Describe the relationship between the graphs \(g(x)\) and \(G(x)\).
Give the domain and range of \(H(x)\).
For \(y={\left(\dfrac{1}{k}\right)}^{x}\) and \(k>1\), the greater the value of \(k\), the steeper the curve of the graph. True or false?
Give the equation of the asymptote for the functions.
|
\(-\text{2}\) |
\(-\text{1}\) |
\(\text{0}\) |
\(\text{1}\) |
\(\text{2}\) |
|
|
\(f(x)={2}^{x}\) |
\(\frac{1}{4}\) |
\(\frac{1}{2}\) |
\(\text{1}\) |
\(\text{2}\) |
\(\text{4}\) |
|
\(g(x)={3}^{x}\) |
\(\frac{1}{9}\) |
\(\frac{1}{3}\) |
\(\text{1}\) |
\(\text{3}\) |
\(\text{9}\) |
|
\(h(x)={5}^{x}\) |
\(\frac{1}{25}\) |
\(\frac{1}{5}\) |
\(\text{1}\) |
\(\text{5}\) |
\(\text{25}\) |
|
\(-\text{2}\) |
\(-\text{1}\) |
\(\text{0}\) |
\(\text{1}\) |
\(\text{2}\) |
|
|
\(F(x)={\left(\frac{1}{2}\right)}^{x}\) |
\(\text{4}\) |
\(\text{2}\) |
\(\text{1}\) |
\(\frac{1}{2}\) |
\(\frac{1}{4}\) |
|
\(G(x)={\left(\frac{1}{3}\right)}^{x}\) |
\(\text{9}\) |
\(\text{3}\) |
\(\text{1}\) |
\(\frac{1}{3}\) |
\(\frac{1}{9}\) |
|
\(H(x)={\left(\frac{1}{5}\right)}^{x}\) |
\(\text{25}\) |
\(\text{5}\) |
\(\text{1}\) |
\(\frac{1}{5}\) |
\(\frac{1}{25}\) |
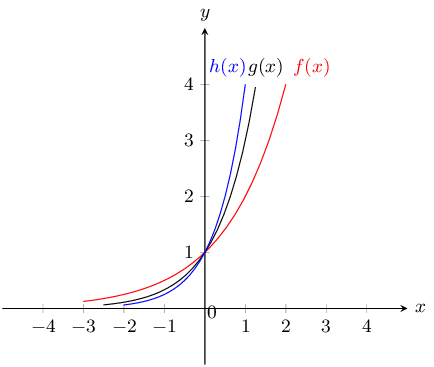
We notice that all graphs pass through the point \((0;1)\). Any number with exponent \(\text{0}\) is equal to \(\text{1}\).
The graphs do not cut the \(x\)-axis because you can never get \(\text{0}\) by raising any non-zero number to the power of any other number.
Domain: \(\left\{x:x\in \mathbb{R}\right\}\)
Range: \(\left\{y:y\in \mathbb{R}, y>0\right\}\)
As \(x\) increases, \(h(x)\) increases.
\(f(x)={2}^{x}\) increases at the slowest rate because it has the smallest base.
True: the greater the value of \(k\) \(\left(k>1\right)\), the steeper the graph of \(y={k}^{x}\).
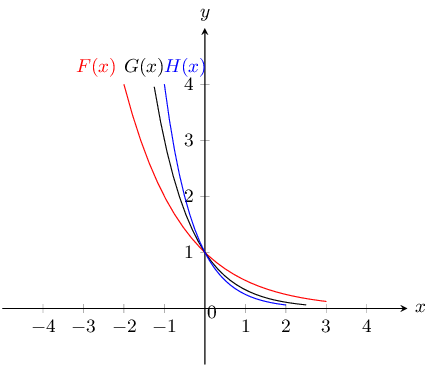
The \(y\)-intercept is the point \((0;1)\) for all graphs. For any real number \(z\): \({z}^{0}=1 \qquad z \ne 0\).
\(F(x)\) is the reflection of \(f(x)\) about the \(y\)-axis.
\(G(x)\) is the reflection of \(g(x)\) about the \(y\)-axis.
Domain: \(\left\{x:x\in \mathbb{R}\right\}\)
Range: \(\left\{y:y\in \mathbb{R}, y>0\right\}\)
True: the greater the value of \(k\) \(\left(k>1\right)\), the steeper the graph of \(y={\left(\frac{1}{k}\right)}^{x}\).
The equation of the horizontal asymptote is \(y=0\), the \(x\)-axis.
CAPS states to only investigate the effects of \(a\) and \(q\) on an exponential graph. However it is also important for learners to see that \(b\) has a different effect on the graph depending on if \(b > 1\) or \(0 < b < 1\).
For this reason the effect of \(b\) is included in the investigation so that learners can see what happens when \(b > 1\) and when \(0 < b < 1\).
Also note that the above worked example further reinforces the effects of \(b\) on the exponential graph.
On the same set of axes, plot the following graphs (\(a=1\), \(q=0\) and \(b\) changes):
\(y_{1} = 2^{x}\)
\(y_{2} = \left(\frac{1}{2}\right)^{x}\)
\(y_{3} = 6^{x}\)
\(y_{4} = \left(\frac{1}{6}\right)^{x}\)
|
\(-\text{2}\) |
\(-\text{1}\) |
\(\text{0}\) |
\(\text{1}\) |
\(\text{2}\) |
|
|
\(y_{1}=2^{x}\) |
|||||
|
\(y_{2}=\left(\frac{1}{2}\right)^{x}\) |
|||||
|
\(y_{3}=6^{x}\) |
|||||
|
\(y_{4}=\left(\frac{1}{6}\right)^{x}\) |
Use your results to deduce the effect of \(b\).
On the same set of axes, plot the following graphs (\(b=2\), \(a=1\) and \(q\) changes):
\({y}_{5}={2}^{x}-2\)
\({y}_{6}={2}^{x}-1\)
\({y}_{7}={2}^{x}\)
\({y}_{8}={2}^{x}+1\)
\({y}_{9}={2}^{x}+2\)
|
\(-\text{2}\) |
\(-\text{1}\) |
\(\text{0}\) |
\(\text{1}\) |
\(\text{2}\) |
|
|
\({y}_{5}={2}^{x}-2\) |
|||||
|
\({y}_{6}={2}^{x}-1\) |
|||||
|
\({y}_{7}={2}^{x}\) |
|||||
|
\({y}_{8}={2}^{x}+1\) |
|||||
|
\({y}_{9}={2}^{x}+2\) |
Use your results to deduce the effect of \(q\).
On the same set of axes, plot the following graphs (\(b=2\), \(q=0\) and \(a\) changes).
\({y}_{10}=1 \times {2}^{x}\)
\({y}_{11}=2\times {2}^{x}\)
\({y}_{12}=-1 \times {2}^{x}\)
\({y}_{13}=-2\times {2}^{x}\)
|
\(-\text{2}\) |
\(-\text{1}\) |
\(\text{0}\) |
\(\text{1}\) |
\(\text{2}\) |
|
|
\({y}_{10}=1 \times {2}^{x}\) |
|||||
|
\({y}_{11}=2\times {2}^{x}\) |
|||||
|
\({y}_{12}=-1 \times {2}^{x}\) |
|||||
|
\({y}_{13}=-2\times {2}^{x}\) |
Use your results to deduce the effect of \(a\).
The effect of \(q\)
The effect of \(q\) is called a vertical shift because all points are moved the same distance in the same direction (it slides the entire graph up or down).
For \(q>0\), the graph is shifted vertically upwards by \(q\) units.
For \(q<0\), the graph is shifted vertically downwards by \(q\) units.
The horizontal asymptote is shifted by \(q\) units and is the line \(y=q\).
The effect of \(a\)
The sign of \(a\) determines whether the graph curves upwards or downwards.
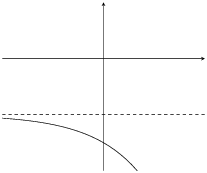
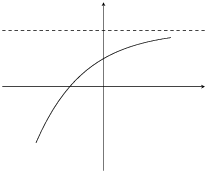
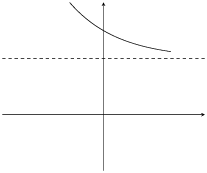
For \(0 < b < 1\):
For \(a>0\), the graph curves downwards. It reflects the graph about the horizontal asymptote.
For \(a<0\), the graph curves upwards.
For \(b > 1\):
For \(a>0\), the graph curves upwards.
For \(a<0\), the graph curves downwards. It reflects the graph about the horizontal asymptote.
|
\(b>1\) |
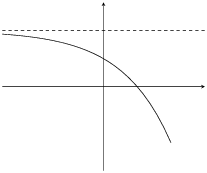
\(a<0\) |
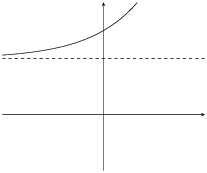
\(a>0\) |
|
\(q>0\) |
 |
 |
|
\(q<0\) |
 |
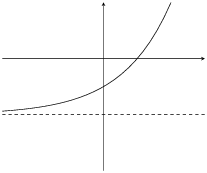 |
The effect of \(a\) and \(q\) on an exponential graph when \(b > 1\).
|
\(0<b<1\) |
\(a<0\) |
\(a>0\) |
|
\(q>0\) |
 |
 |
|
\(q<0\) |
 |
 |
The effect of \(a\) and \(q\) on an exponential graph when \(0 < b < 1\).
The standard form of an exponential function is \(y=a{b}^{x}+q\).
For \(y=a{b}^{x}+q\), the function is defined for all real values of \(x\). Therefore the domain is \(\left\{x:x\in \mathbb{R}\right\}\).
The range of \(y=a{b}^{x}+q\) is dependent on the sign of \(a\).
For \(a>0\):
\begin{align*} {b}^{x}& > 0 \\ a{b}^{x}& > 0 \\ a{b}^{x}+q& > q \\ f(x)& > q \end{align*}Therefore, for \(a>0\) the range is \(\left\{f(x):f(x)>q\right\}\).
For \(a<0\):
\begin{align*} {b}^{x}& > 0 \\ a{b}^{x}& < 0 \\ a{b}^{x}+q& < q \\ f(x)& < q \end{align*}Therefore, for \(a<0\) the range is \(\left\{f(x):f(x)<q\right\}\).
Find the domain and range of \(g(x)=5 \cdot {2}^{x}+1\)
The domain of \(g(x)=5\times {2}^{x}+1\) is \(\left\{x:x\in \mathbb{R}\right\}\).
Therefore the range is \(\left\{g(x):g(x)>1\right\}\).
The \(y\)-intercept.
For the \(y\)-intercept, let \(x=0\):
\begin{align*} y& = a{b}^{x}+q \\ & = a{b}^{0}+q \\ & = a(1)+q \\ & = a+q \end{align*}For example, the \(y\)-intercept of \(g(x)=5\times {2}^{x}+1\) is given by setting \(x=0\):
\begin{align*} y& = 5\times {2}^{x}+1 \\ & = 5\times {2}^{0}+1 \\ & = 5+1 \\ & = 6 \end{align*}This gives the point \((0;6)\).
The \(x\)-intercept:
For the \(x\)-intercept, let \(y=0\).
For example, the \(x\)-intercept of \(g(x)=5\times {2}^{x}+1\) is given by setting \(y=0\):
\begin{align*} y& = 5\times {2}^{x}+1 \\ 0& = 5\times {2}^{x}+1 \\ -1& = 5\times {2}^{x} \\ {2}^{x}& = -\frac{1}{5} \end{align*}There is no real solution. Therefore, the graph of \(g(x)\) does not have any \(x\)-intercepts.
Exponential functions of the form \(y=a{b}^{x}+q\) have a single horizontal asymptote, the line \(x=q\).
In order to sketch graphs of functions of the form, \(y=a{b}^{x}+q\), we need to determine four characteristics:
sign of \(a\)
\(y\)-intercept
\(x\)-intercept
asymptote
The following video shows some examples of sketching exponential functions.
Sketch the graph of \(g(x)=3\times {2}^{x}+2\). Mark the intercept and the asymptote.
From the equation we see that \(a>1\), therefore the graph curves upwards. \(q>0\) therefore the graph is shifted vertically upwards by \(\text{2}\) units.
For the \(y\)-intercept, let \(x=0\):
\begin{align*} y& = 3\times {2}^{x}+2 \\ & = 3\times {2}^{0}+2 \\ & = 3+2 \\ & = 5 \end{align*}This gives the point \((0;5)\).
For the \(x\)-intercept, let \(y=0\):
\begin{align*} y& = 3\times {2}^{x}+2 \\ 0& = 3\times {2}^{x}+2 \\ -2& = 3\times {2}^{x} \\ {2}^{x}& = -\frac{2}{3} \end{align*}There is no real solution, therefore there is no \(x\)-intercept.
The horizontal asymptote is the line \(y=2\).

Domain: \(\left\{x:x\in \mathbb{R}\right\}\)
Range: \(\left\{g(x):g(x)>2\right\}\)
Note that there is no axis of symmetry for exponential functions.
Sketch the graph of \(y=-2\times {3}^{x}+6\)
From the equation we see that \(a<0\) therefore the graph curves downwards. \(q>0\) therefore the graph is shifted vertically upwards by \(\text{6}\) units.
For the \(y\)-intercept, let \(x=0\):
\begin{align*} y& = -2\times {3}^{x}+6 \\ & = -2\times {3}^{0}+6 \\ & = 4 \end{align*}This gives the point \((0;4)\).
For the \(x\)-intercept, let \(y=0\):
\begin{align*} y& = -2\times {3}^{x}+6 \\ 0& = -2\times {3}^{x}+6 \\ -6& = -2\times {3}^{x} \\ {3}^{1}& = {3}^{x} \\ \therefore x& = 1 \end{align*}This gives the point \((1;0)\).
The horizontal asymptote is the line \(y=6\).
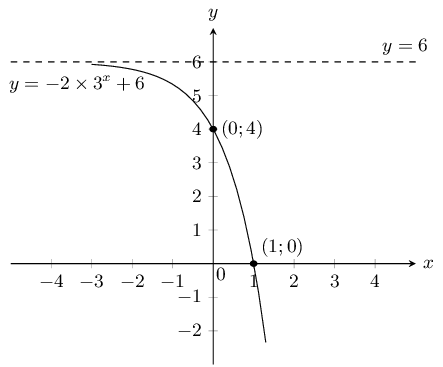
Domain: \(\left\{x:x\in \mathbb{R}\right\}\)
Range: \(\left\{g(x):g(x)<6\right\}\)
Given the following equation:
\(y = -\frac{2}{3}. (\text{3})^{x} + 1\)
Calculate the \(y\)-intercept. Your answer must be correct to 2 decimal places.
The \(y\)-intercept is \((0;\text{0,33})\).
Now calculate the \(x\)-intercept. Estimate your answer to one decimal place if necessary.
We calculate the \(x\)-intercept by letting \(y = 0\). Then we solve for \(x\):
\begin{align*} 0 & = \left( -\frac{2}{3} \right). (\text{3})^{x} + \text{1} \\ -\text{1} & = \left( -\frac{2}{3} \right)(\text{3})^{x} \\ \left( - \frac{3}{2} \right) (-\text{1}) & = \left( - \frac{3}{2} \right) \left( - \frac{2}{3} \right). (\text{3})^{x} \\ \frac{3}{2} & = \text{3}^{x} \end{align*}To find the answer we try different values of \(x\):
\begin{align*} \text{Try: } \text{3}^{-1} & = \text{0,333...}\\ \text{Try: } \text{3}^0 & = \text{1}\\ \text{Try: } \text{3}^1 & = \text{3} \end{align*}We can see that the exponent must be between 0 and 1. Next we try values starting with \(\text{0,1}\) and see what the value of the exponent is. Doing this we find that \(x = \text{0,4}\).
The \(x\)-intercept is \((\text{0,4};0)\).
The graph here shows an exponential function with the equation \(y = a \cdot 2^{x} + q\). One point is given on the curve: Point A is at \((-3;\text{3,875})\). Determine the values of \(a\) and \(q\), correct to the nearest integer.

The asymptote lies at \(y = 4\). Therefore \(q\) is 4.
At this point we know that the equation for the graph must be \(y = a \cdot 2^{x} + 4\).
\begin{align*} y & = a (2)^{x} + 4 \\ (\text{3,875}) & = a (2)^{(-3)} + 4 \\ \text{3,875} - 4 & = a (2)^{\left(-3\right)} \\ -\text{0,125} & = a (\text{0,125}) \\ -1 & = a \end{align*}Therefore \(a = -1 \text{ and } q = 4\)
Below you see a graph of an exponential function with the equation \(y = a \cdot 2^{x} + q\). One point is given on the curve: Point A is at \((-3;\text{4,875})\). Calculate the values of \(a\) and \(q\), correct to the nearest integer.

The asymptote lies at \(y = 5\). Therefore \(q\) is 5.
At this point we know that the equation for the graph must be \(y = a \cdot 2^{x} + 5\).
\begin{align*} y & = a (2)^{x} + 5 \\ (\text{4,875}) & = a (2)^{ (-3)} + 5 \\ \text{4,875} - 5 & = a (2)^{\left(-3\right)} \\ -\text{0,125} & = a (\text{0,125}) \\ -1 & = a \end{align*}Therefore \(a = -1 \text{ and } q = 5\).
Given the following equation:
\(y = \dfrac{1}{4} \cdot (4)^{x} - 1\)
Calculate the \(y\)-intercept. Your answer must be correct to 2 decimal places.
Therefore the \(y\)-intercept is \((0;-\text{0,75})\).
Now calculate the \(x\)-intercept.
We calculate the \(x\)-intercept by letting \(y = 0\). Then start to solve for \(x\).
\begin{align*} 0 & = \left( \frac{1}{4} \right) \cdot (4)^{x} - 1 \\ 1 & = \left( \frac{1}{4} \right) \cdot (4)^{x} \\ \left( 4 \right) (1) & = \left( 4 \right) \left( \frac{1}{4} \right) \cdot (4)^{x} \\ 4^1 & = 4^{x} \\ x &= 1 \end{align*}Therefore the \(x\)-intercept is \((1;0)\).
Given the following graph, identify a function that matches each of the following equations:

\(y = 2^x\)
\(y = -2^x\)
\(y = 2 \cdot 2^x\)
\(y = \left(\frac{1}{2}\right)^{x}\)
Given the functions \(y=2^{x}\) and \(y=\left(\frac{1}{2}\right)^{x}\).
Draw the graphs on the same set of axes.
For \(y=2^{x}\):
\(a\) is positive and greater than 1 and so the graph curves upwards. The \(y\)-intercept is \((0;1)\). There is no \(x\)-intercept. The asymptote is the line \(x = 0\).
For \(y=\left(\frac{1}{2}\right)^{x}\):
\(a\) is positive and less than 1 and so the graph curves downwards. The \(y\)-intercept is \((0;1)\). There is no \(x\)-intercept. The asymptote is the line \(x = 0\).
The graph is:
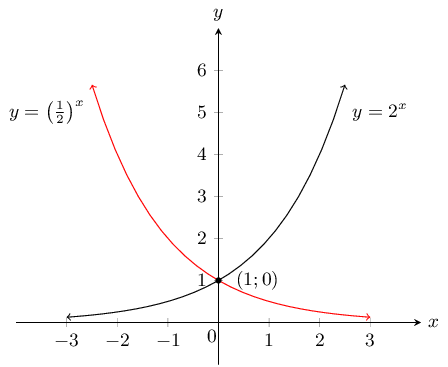
Is the \(x\)-axis an asymptote or an axis of symmetry to both graphs? Explain your answer.
The \(x\)-axis is an asymptote to both graphs because both approach the \(x\)-axis but never touch it.
Which graph can be described by the equation \(y=2^{-x}\)? Explain your answer.
\(y= \left(\frac{1}{2}\right)^{x}\) can be described by the equation \(y=2^{-x}\) because \(y=\left(\frac{1}{2}\right)^x = \left(2^{-1} \right)^x = 2^{-x}\).
Solve the equation \(2^{x} = \left(\frac{1}{2}\right)^{x}\) graphically and check your answer is correct by using substitution.
The graphs intersect at the point \((0;1)\). If we substitute these values into each side of the equation we get:
\begin{align*} \text{LHS: } 2^{x} & = 2^0 = 1 \text{ and} \\ \text{RHS: } (\frac{1}{2})^x & = (\frac{1}{2})^0 = 1 \end{align*}LHS = RHS, therefore the answer is correct.
The curve of the exponential function \(f\) in the accompanying diagram cuts the \(y\)-axis at the point \(A(0;1)\) and passes through the point \(B(2;9)\).
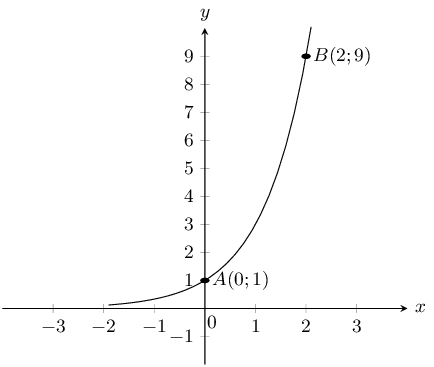
Determine the equation of the function \(f\).
The general form of the equation is \(f(x)=a \cdot b^x+q\).
We are given \(A(0; 1)\) and \(B(2; 9)\).
The asymptote is at \(y = 0\) and so \(q = 0\).
Substitute in the values of point \(A\):
\begin{align*} 1 & = a \cdot b^0 \\ 1 & = a \end{align*}Substitute in the values of point \(B\):
\begin{align*} 9 & = b^2 \\ 3^2 & = b^2\\ \therefore b & = 3 \end{align*}Therefore the equation is \(f(x) = 3^x\).
Determine the equation of the function \(h(x)\), the reflection of \(f(x)\) in the \(x\)-axis.
\(h(x)=-3^{x}\)
Determine the range of \(h(x)\).
Range: \((-\infty;0)\)
Determine the equation of the function \(g(x)\), the reflection of \(f(x)\) in the \(y\)-axis.
\(g(x)=3^{-x}\)
Determine the equation of the function \(j(x)\) if \(j(x)\) is a vertical stretch of \(f(x)\) by \(+2\) units.
\(j(x)=2 \cdot 3^{x}\)
Determine the equation of the function \(k(x)\) if \(k(x)\) is a vertical shift of \(f(x)\) by \(-3\) units.
\(k(x)=3^{x}-3\)
|
Previous
6.4 Hyperbolic functions
|
Table of Contents |
Next
6.6 Trigonometric functions
|