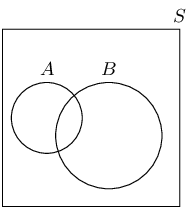
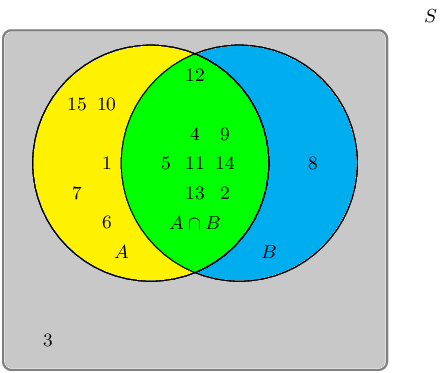
A group of learners are given the following Venn diagram:
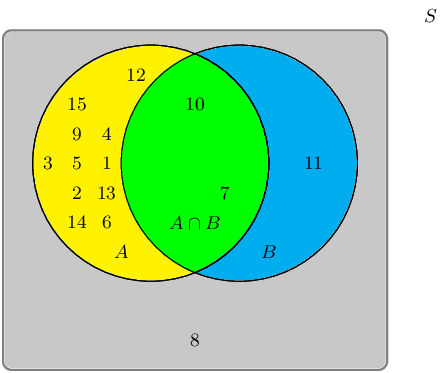
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n \leq 15 \}\).
They are asked to identify the event set of the intersection between event set \(A\) and event set \(B\), also written as \(A \cap B\). They get stuck, and you offer to help them find it.
Which set best describes the event set of \(A \cap B\)?
- \(\{7;10;11\}\)
- \(\{1;2;3;4;5;6;7;9;10;11\}\)
- \(\{1;2;3;4;5;6;7;9;10\}\)
- \(\{7;10\}\)
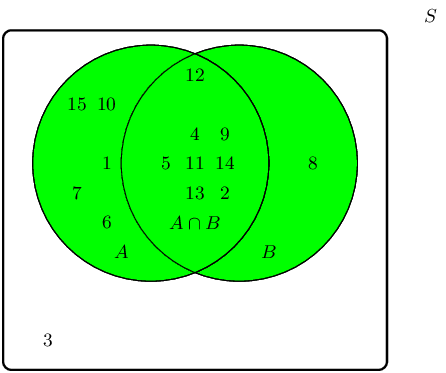
The intersection between event set \(A\) and event set \(B\), also written as \(A \cap B\), can be shaded as follows:
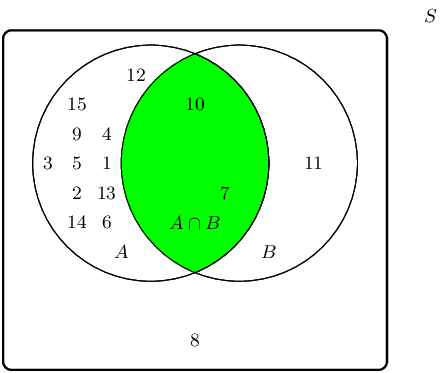
Therefore the event set \(\{7;10\}\) best describes the event set of \(A \cap B\).