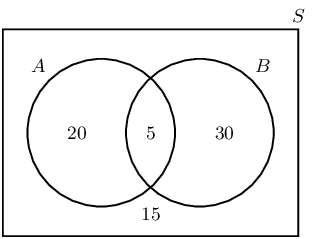
A group of learners are given the following Venn diagram:
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n
\leq 15 \}\).
They are asked to identify the complementary event set of \(B\), also known as \(B'\). They get stuck,
and you offer to help them find it.
Which of the following sets best describes the event set of \(B'\)?
- \(\{1;5;13;14\}\)
- \(\{2;3;4;6;10;11;12\}\)
- \(\{3;4;6;11;12\}\)
The event set \(B\) can be shaded as follows:
The complementary event set \(B'\) can be shaded as follows:
Therefore the event set \(\{2;3;4;6;10;11;12\}\) best describes the complementary event set of \(B\),
also known as \(B'\).
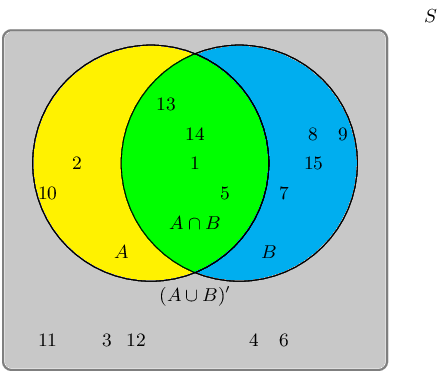
A group of learners are given the following Venn diagram:
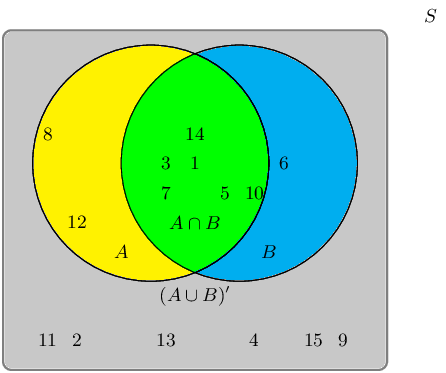
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n
\leq 15 \}\).
They are asked to identify the complementary event set of \((A \cup B)\), also known as \((A \cup B)'\).
They get stuck, and you offer to help them find it.
Which of the following sets best describes the event set of \((A \cup B)'\)?
- \(\{2;4;9;11;13;15\}\)
- \(\{1;3;5;6;7;8;10;12;14\}\)
- \(\{6;8;12\}\)
The event set \((A \cup B)\) can be shaded as follows:
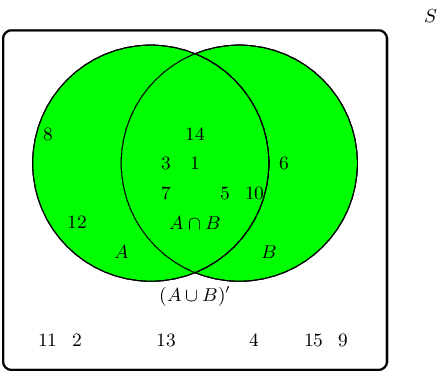
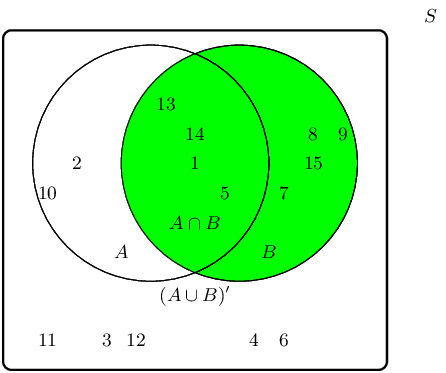
The complementary event set \((A \cup B)'\) can be shaded as follows:
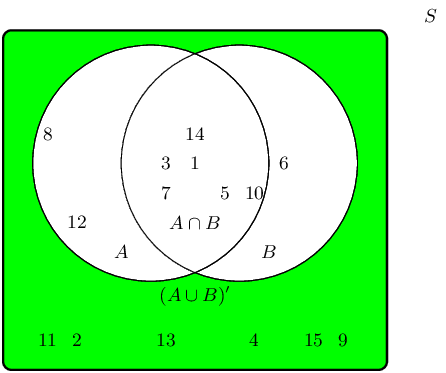
Therefore the event set \(\{2;4;9;11;13;15\}\) best describes the complementary event set of \((A \cup
B)\), also known as \((A \cup B)'\).
Given the following Venn diagram:
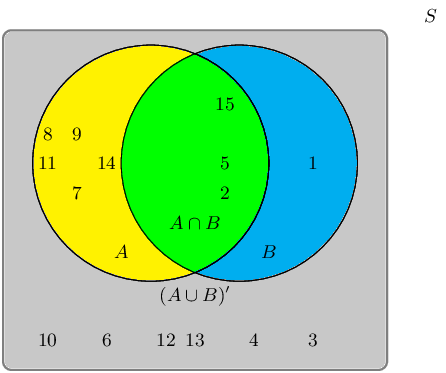
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n
\leq 15 \}\).
Are \((A \cup B)'\) and \(A \cup B\) mutually exclusive?
We recall the definition of the term “mutually exclusive”:
Two events are called mutually exclusive if they cannot occur at the same time.
The event set for \((A \cup B)'\) is: \(\{3;4;10;12;13\}\)
The event set for \(A \cup B\) is: \(\{1;2;5;6;7;8;9;11;14;15\}\)
The question we must ask: Can they occur at the same time?
By observing both sets, we can identify the following overlapping event set: \(\{\} \text{ or }
\varnothing\).
Therefore, yes, the event sets \((A \cup B)'\) and \(A \cup B\) are mutually exclusive in this example.
Given the following Venn diagram:
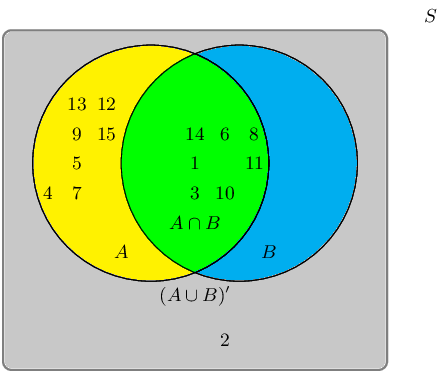
The sample space can be described as \(\{ n:n \text{ } \epsilon \text{ } \mathbb{Z}, \text{ } 1 \leq n
\leq 15 \}\).
Are \(A'\) and \(B'\) mutually exclusive?
We recall the definition of the term “mutually exclusive”:
Two events are called mutually exclusive if they cannot occur at the same time.
The event set for \(A'\) is: \(\{2\}\)
The event set for \(B'\) is: \(\{2;4;5;7;9;12;13;15\}\)
The question we must ask: Can they occur at the same time?
By observing both sets, we can identify the following overlapping event set: \(\{2\}\)
Therefore, no, the event sets \(A'\) and \(B'\) are not mutually exclusive in this example.