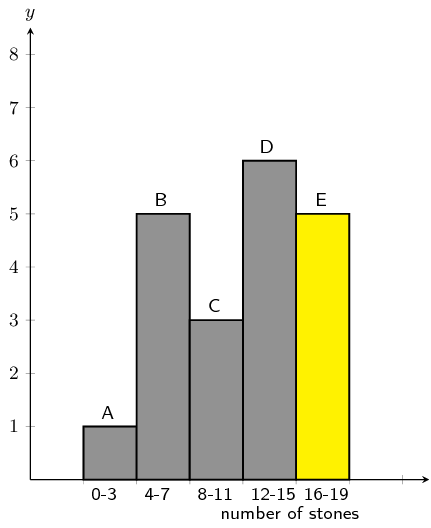
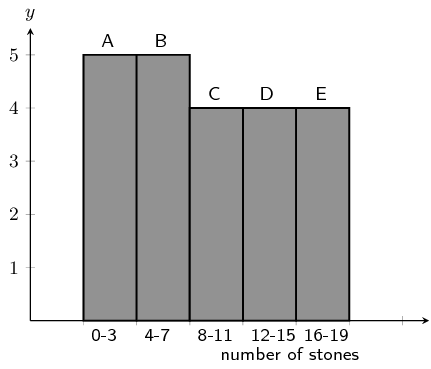
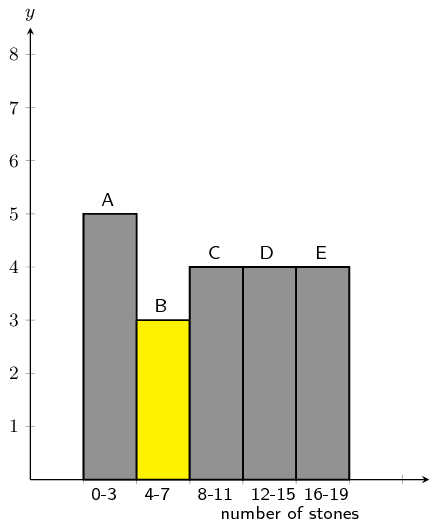
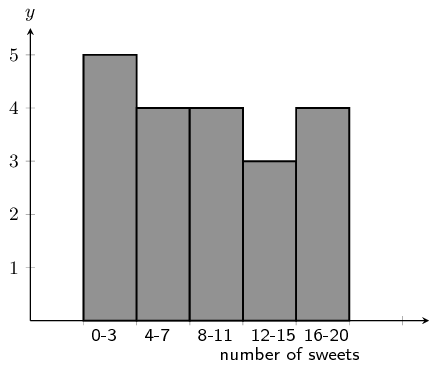
Consider the following grouped data and calculate the mean, the modal group and the median group.
|
Mass (\(\text{kg}\))
|
Count
|
|
\(40 < m \le 45\)
|
\(\text{7}\)
|
|
\(45 < m \le 50\)
|
\(\text{10}\)
|
|
\(50 < m \le 55\)
|
\(\text{15}\)
|
|
\(55 < m \le 60\)
|
\(\text{12}\)
|
|
\(60 < m \le 65\)
|
\(\text{6}\)
|
To find the mean we use the middle value for each group. The count then tells us how many times that
value occurs in the data set. Therefore the mean is:
\begin{align*}
\text{mean } & = \frac{7(43) + 10(48) + 15(53) + 12(58) + 6(63)}{7 + 10 + 15 + 12 + 6} \\
& = \frac{2650}{50} \\
& = 53
\end{align*}
The modal group is the group with the highest number of data values. This is \(50 <m \le 55\) with
15 data values.
The median group is the central group. There are 5 groups and so the central group is the third one:
\(50 <m \le 55\).
Mean: \(\text{52}\); Modal group: \(50 <m \le 55\); Median group: \(50 < m \le 55\).
Find the mean, the modal group and the median group in this data set of how much time people needed to
complete a game.
|
Time (s)
|
Count
|
|
\(35 < t \le 45\)
|
\(\text{5}\)
|
|
\(45 < t \le 55\)
|
\(\text{11}\)
|
|
\(55 < t \le 65\)
|
\(\text{15}\)
|
|
\(65 < t \le 75\)
|
\(\text{26}\)
|
|
\(75 < t \le 85\)
|
\(\text{19}\)
|
|
\(85 < t \le 95\)
|
\(\text{13}\)
|
|
\(95 < t \le 105\)
|
\(\text{6}\)
|
To find the mean we use the middle value for each group. The count then tells us how many times that
value occurs in the data set. Therefore the mean is:
\begin{align*}
\text{mean } & = \frac{5(\text{40,5}) + 11(\text{50,5}) + 15(\text{60,5}) + 26(\text{70,5}) +
19(\text{80,5}) + 13(\text{90,5}) + 6(\text{100,5})}{5 + 11 + 15 + 26 + 19 + 13 + 6} \\
& = \frac{\text{6 807,5}}{95} \\
& = \text{71,66}
\end{align*}
The modal group is the group with the highest number of data values. This is \(65 <m \le 75\) with
26 data values.
The median group is the central group. There are 7 groups and so the central group is the fourth one:
\(65 <m \le 75\).
Mean: \(\text{70,66}\); Modal group: \(65 < t \le 75\); Median group: \(65 < t \le 75\).