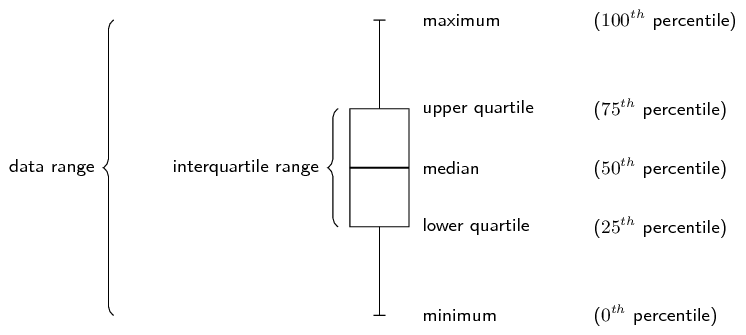
Lisa is working in a computer store. She sells the following number of computers
each month:
\[\left\{27; 39; 3; 15; 43; 27; 19; 54; 65; 23; 45; 16\right\}\]
Give the five number summary and box-and-whisker plot of Lisa's sales.
We first order the data set.
\[\left\{3; 15; 16; 19; 23; 27; 27; 39; 43; 45; 54; 65\right\}\]
Now we can read off the minimum as the first value (\(\text{3}\)) and the maximum
as the last value (\(\text{65}\)).
Next we need to determine the quartiles.
There are \(\text{12}\) values in the data set. Using the percentile formula, we
can determine that the median lies between the sixth and seventh values,
making it:
\[\frac{\text{27} + \text{27}}{2} = \text{27}\]
The first quartile lies between the third and fourth values, making it:
\[\frac{\text{16} + \text{19}}{2} = \text{17,5}\]
The third quartile lies between the ninth and tenth values, making it:
\[\frac{\text{43} + \text{45}}{2} = \text{44}\]
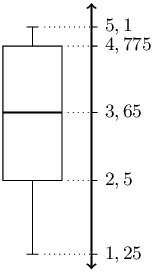
This provides the five number summary of the data set and allows us to draw the
following box-and-whisker plot.
Five number summary:
Minimum: \(3\)
\(Q_1\): \(\text{17,5}\)
Median: \(27\)
\(Q_3\): \(44\)
Maximum: \(65\)
Box-and-whisker plot:
Zithulele works as a telesales person. He keeps a record of the number of sales
he makes each month. The data below show how much he sells each month.
\[\left\{49; 12; 22; 35; 2; 45; 60; 48; 19; 1; 43; 12\right\}\]
Give the five number summary and box-and-whisker plot of Zithulele's sales.
We first order the data set.
\[\left\{1; 2; 12; 12; 19; 22; 35; 43; 45; 48; 49; 60\right\}\]
Now we can read off the minimum as the first value (\(\text{1}\)) and the maximum
as the last value (\(\text{60}\)).
Next we need to determine the quartiles.
There are \(\text{12}\) values in the data set. Using the percentile formula, we
can determine that the median lies between the sixth and seventh values,
making it:
\[\frac{\text{22} + \text{35}}{2} = \text{28,5}\]
The first quartile lies between the third and fourth values, making it:
\[\frac{\text{12} + \text{12}}{2} = \text{12}\]
The third quartile lies between the ninth and tenth values, making it:
\[\frac{\text{45} + \text{48}}{2} = \text{46,5}\]
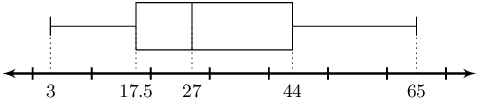
The five number summary is:
Minimum: \(1\)
\(Q_1\): \(12\)
Median: \(\text{28,5}\)
\(Q_3\): \(\text{46,5}\)
Maximum: \(60\)
The box and whisker plot is:
Nombusa has worked as a florist for nine months. She sold the following number of
wedding bouquets:
\[\left\{16; 14; 8; 12; 6; 5; 3; 5; 7\right\}\]
Give the five number summary of Nombusa's sales.
We first order the data set.
\[\left\{3; 5; 5; 6; 7; 8; 12; 14; 16\right\}\]
Now we can read off the minimum as the first value (\(\text{3}\)) and the maximum
as the last value (\(\text{16}\)).
Next we need to determine the quartiles.
There are \(\text{9}\) values in the data set. Using the percentile formula, we
can determine that the median lies at the fifth value, making it \(\text{7}\).
The first quartile lies at the third value, making it \(\text{5}\).
The third quartile lies at the seventh values, making it \(\text{12}\).
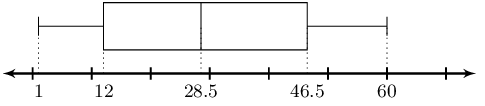
The five number summary is:
Minimum: \(3\)
\(Q_1\): \(5\)
Median: \(7\)
\(Q_3\): \(12\)
Maximum: \(16\)