5.2 Similarity of triangles | Trigonometry

temp text

5.2 Similarity of triangles (EMA3N)

Before we delve into the theory of trigonometry, complete the following investigation to get a better understanding of the foundation of trigonometry.

Ratios of similar triangles

Draw three similar triangles of different sizes using a protractor and a ruler, with each triangle having interior angles equal to \(\text{30}\)°, \(\text{90}\)° and \(\text{60}\)° as shown below. Measure the angles and lengths accurately in order to fill in the table (leave your answers as a simplified fraction):

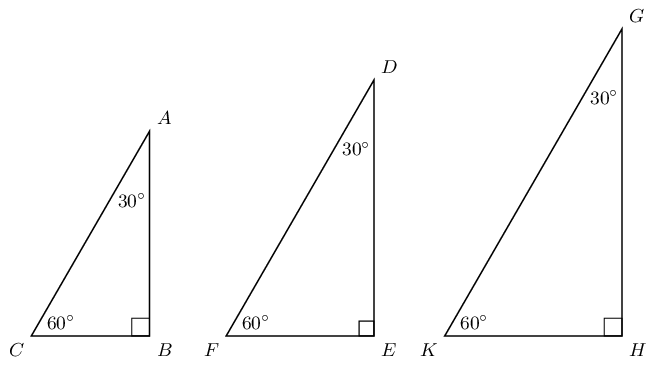
Dividing lengths of sides (ratios)
\(\frac{AB}{BC}=\)	\(\frac{AB}{AC}=\)	\(\frac{CB}{AC}=\)
\(\frac{DE}{EF}=\)	\(\frac{DE}{DF}=\)	\(\frac{FE}{DF}=\)
\(\frac{GH}{HK}=\)	\(\frac{GH}{GK}=\)	\(\frac{KH}{GK}=\)

What observations can you make about the ratios of the sides?

Have you noticed that it does not matter what the lengths of the sides of the triangles are, if the angle remains constant, the ratio of the sides will always yield the same answer?

In the triangles below, \(\triangle ABC\) is similar to \(\triangle DEF\). This is written as:

\(\triangle ABC ||| \triangle DEF\)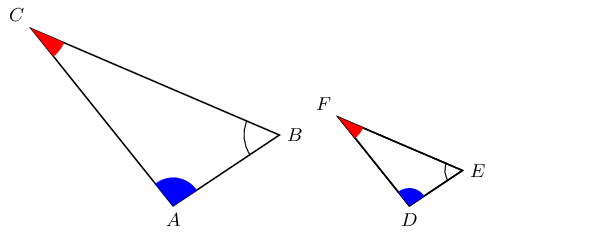

In similar triangles, it is possible to deduce ratios between corresponding sides:

\begin{align*} \frac{AB}{BC} & = \frac{DE}{EF} \\ \frac{AB}{AC} & = \frac{DE}{DF} \\ \frac{AC}{BC} & = \frac{DF}{EF} \\ \frac{AB}{DE} & = \frac{BC}{EF} = \frac{AC}{DF} \end{align*}

Another important fact about similar triangles \(ABC\) and \(DEF\) is that the angle at vertex \(A\) is equal to the angle at vertex \(D\), the angle at vertex \(B\) is equal to the angle at vertex \(E\), and the angle at vertex \(C\) is equal to the angle at vertex \(F\).

\begin{align*} \hat{A} & = \hat{D} \\ \hat{B} & = \hat{E} \\ \hat{C} & = \hat{F} \end{align*}

The order of letters for similar triangles is very important. Always label similar triangles in corresponding order. For example,

\begin{align*} \triangle ABC ||| \triangle DEF &\text{ is correct; but } \\ \triangle ABC ||| \triangle DFE & \text{ is incorrect.} \end{align*}

5.1 Introduction

Table of Contents

5.3 Defining the trigonometric ratios