\(OB\)
\(OB\) is the hypotenuse of \(\triangle BOX\). We can calculate the length of \(OB\) using the theorem of Pythagoras:
\begin{align*} OB^{2} & = OX^{2} + XB^{2} \\ & = (1)^{2} + (3)^{2} \\ & = 10 \\ OB & = \sqrt{10} \end{align*}|
Previous
5.7 Solving trigonometric equations
|
Next
5.9 Chapter summary
|
We have defined the trigonometric ratios using right-angled triangles. We can extend these definitions to any angle, noting that the definitions do not rely on the lengths of the sides of the triangle, but on the size of the angle only. So if we plot any point on the Cartesian plane and then draw a line from the origin to that point, we can work out the angle between the \(x\)-axis and that line. We will first look at this for two specific points and then look at the more general case.
Finding an angle for specific points
In the figure below points \(P\) and \(Q\) have been plotted. A line from the origin (\(O\)) to each point is drawn. The dotted lines show how we can construct right-angled triangles for each point. The dotted line must always be drawn to the \(x\)-axis. Now we can find the angles \(A\) and \(B\):
We can also extend the definitions of the reciprocals in the same way.

From the coordinates of \(P\left(2;3\right)\), we can see that \(x=2\) and \(y=3\). Therefore, we know the length of the side opposite \(\hat{A}\) is \(\text{3}\) and the length of the adjacent side is \(\text{2}\). Using: \[\tan\hat{A} = \frac{\text{opposite}}{\text{adjacent}} = \frac{3}{2}\] we calculate that \(\hat{A} = \text{56,3}°\).
We can also use the theorem of Pythagoras to calculate the hypotenuse of the triangle and then calculate \(\hat{A}\) using: \[\sin\hat{A} = \frac{\text{opposite}}{\text{hypotenuse}} \qquad \text{ or } \qquad \cos\hat{A} = \frac{\text{adjacent}}{\text{hypotenuse}}\]
Consider point \(Q\left(-2;3\right)\). We define \(\hat{B}\) as the angle formed between line \(OQ\) and the positive \(x\)-axis. This is called the standard position of an angle. Angles are always measured from the positive \(x\)-axis in an anti-clockwise direction. Let \(\alpha\) be the angle formed between the line \(OQ\) and the negative \(x\)-axis such that \(\hat{B} + \alpha = 180°\).
From the coordinates of \(Q\left(-2;3\right)\), we know the length of the side opposite \(\alpha\) is \(\text{3}\) and the length of the adjacent side is \(\text{2}\). Using: \[\tan\alpha = \frac{\text{opposite}}{\text{adjacent}} = \frac{3}{2}\] we calculate that \(\alpha = \text{56,3}°\). Therefore \(\hat{B} = 180° - \alpha = \text{123,7}°\).
Similarly, an alternative method is to calculate the hypotenuse using the theorem of Pythagoras and calculate \(\alpha\) using: \[\sin\alpha = \frac{\text{opposite}}{\text{hypotenuse}} \qquad \text{ or } \qquad \cos\alpha = \frac{\text{adjacent}}{\text{hypotenuse}}\]
Finding any angle
If we were to draw a circle centred on the origin (\(O\)) and passing through the point \(P(x;y)\), then the length from the origin to point \(P\) is the radius of the circle, which we denote \(r\). We denote the angle formed between the line \(OP\) and the \(x\)-axis as \(\theta\).
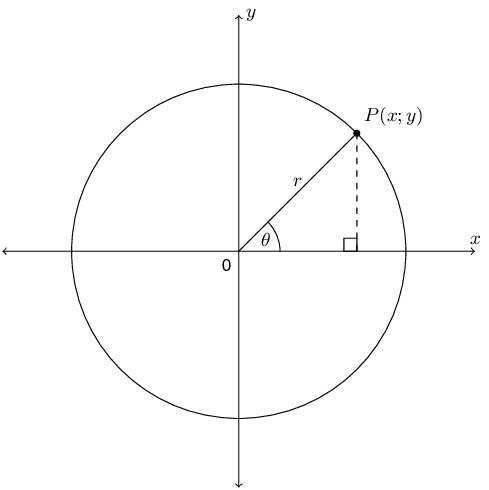
We can rewrite all the trigonometric ratios in terms of \(x\), \(y\) and \(r\). The general definitions for the trigonometric ratios are:
\[\begin{array}{cccc} \sin \theta & = \dfrac{y}{r} & \text{ cosec }\theta & = \dfrac{r}{y} \\ \\ \cos \theta & = \dfrac{x}{r} & \sec\theta & = \dfrac{r}{x} \\ \\ \tan \theta & = \dfrac{y}{x} & \cot \theta & = \dfrac{x}{y} \end{array}\]The CAST diagram
The Cartesian plane is divided into \(\text{4}\) quadrants in an anti-clockwise direction as shown in the diagram below. Notice that \(r\) is always positive but the values of \(x\) and \(y\) change depending on the position of the point in the Cartesian plane. As a result, the trigonometric ratios can be positive or negative. The letters C, A, S and T indicate which of the ratios are positive in each quadrant:
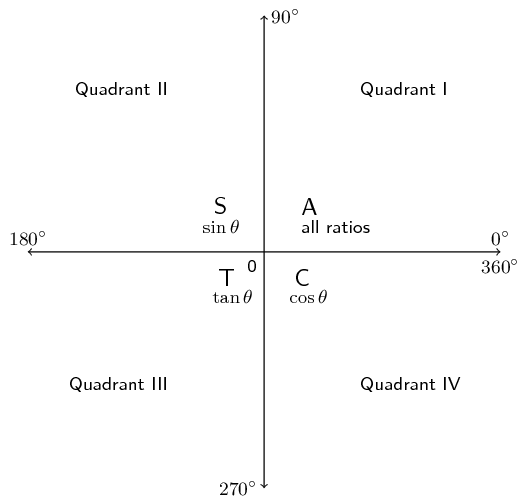
This diagram is known as the CAST diagram.
We note the following using the general definitions of the trigonometric ratios:
Quadrant I
Both the \(x\) and \(y\) values are positive so all ratios are positive in this quadrant.
Quadrant II
The \(y\) values are positive therefore \(\sin\) and cosec are positive in this quadrant (recall that \(\sin\) and cosec are defined in terms of \(y\) and \(r\)).
Quadrant III
Both the \(x\) and the \(y\) values are negative therefore \(\tan\) and \(\cot\) are positive in this quadrant (recall that \(\tan\) and \(\cot\) are defined in terms of \(x\) and \(y\)).
Quadrant IV
The \(x\) values are positive therefore \(\cos\) and \(\sec\) are positive in this quadrant (recall that \(\cos\) and \(\sec\) are defined in terms of \(x\) and \(r\)).
The hypotenuse, \(r\), is a length, and is therefore always positive.
The following video provides a summary of the trigonometric ratios in the Cartesian plane.
Special angles in the Cartesian plane
When working in the Cartesian plane we include two other special angles in right-angled triangles: \(\text{0}\)° and \(\text{90}\)°.
Notice that when \(\theta = 0°\) the length of the opposite side is equal to \(\text{0}\) and the length of the adjacent side is equal to the length of the hypotenuse. Therefore:
\begin{align*} \sin 0° & = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{0}{\text{hypotenuse}} = 0 \\ \cos 0° & = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{\text{hypotenuse}}{\text{hypotenuse}} = 1 \\ \tan 0° & = \frac{\text{opposite}}{\text{adjacent}}=\frac{0}{\text{adjacent}} = 0 \end{align*}When \(\theta =90°\) the length of the adjacent side is equal to \(\text{0}\) and the length of the opposite side is equal to the length of the hypotenuse. Therefore:
\begin{align*} \sin 90° & = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{\text{hypotenuse}}{\text{hypotenuse}} = 1 \\ \cos 90° & = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{0}{\text{hypotenuse}} = 0 \\ \tan 90° & = \frac{\text{opposite}}{\text{adjacent}} = \frac{\text{opposite}}{0} = \text{undefined} \end{align*}Now we can extend our knowledge of special angles.
|
\(\theta\) |
\(\text{0}\)° |
\(\text{30}\)° |
\(\text{45}\)° |
\(\text{60}\)° |
\(\text{90}\)° |
|
\(\sin\theta\) |
0 |
\(\dfrac{1}{2}\) |
\(\dfrac{1}{\sqrt{2}}\) |
\(\dfrac{\sqrt{3}}{2}\) |
1 |
|
\(\cos\theta\) |
1 |
\(\dfrac{\sqrt{3}}{2}\) |
\(\dfrac{1}{\sqrt{2}}\) |
\(\dfrac{1}{2}\) |
0 |
|
\(\tan\theta\) |
0 |
\(\dfrac{1}{\sqrt{3}}\) |
1 |
\(\sqrt{3}\) |
undefined |
\(P\left(-3;4\right)\) is a point on the Cartesian plane with origin \(O\). \(\theta\) is the angle between \(OP\) and the positive \(x\)-axis. Without using a calculator, determine the value of:
\(\cos\theta\)
\(3\tan\theta\)
\(\frac{1}{2}\text{cosec }\theta\)
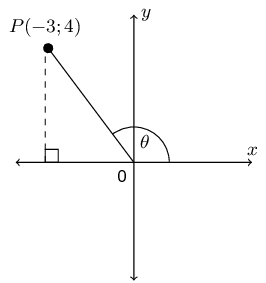
Note \(r\) is positive as it is the radius of the circle.
We note that \(x = -3\), \(y = 4\) and \(r = 5\).
\(\cos\theta = \dfrac{x}{r} = \dfrac{-3}{5}\)
\(3\tan\theta = 3\left(\dfrac{y}{x}\right) = 3\left(\dfrac{4}{-3}\right) = -4\)
\(\dfrac{1}{2}\text{cosec }\theta = \dfrac{1}{2}\left(\dfrac{r}{y}\right) = \frac{1}{2}\left(\dfrac{5}{4}\right) = \dfrac{5}{8}\)
\(X\hat{O}K=\theta\) is an angle in the third quadrant where \(X\) is a point on the positive \(x\)-axis and \(K\) is the point \(\left(-5;y\right)\). \(OK\) is \(\text{13}\) \(\text{units}\).
Determine, without using a calculator, the value of \(y\).
Prove that \({\tan}^{2}\theta + 1 = {\sec}^{2}\theta\) without using a calculator.
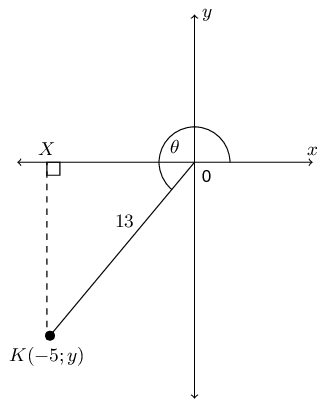
Given that \(\theta\) lies in the third quadrant, \(y\) must be negative.
\[\therefore y = -12\]\(x = -5\), \(y = -12\) and \(r = 13\).
LHS
\begin{align*} {\tan}^{2}\theta + 1 & = {\left(\frac{y}{x}\right)}^{2} + 1 \\ & = {\left(\frac{-12}{-5}\right)}^{2} + 1 \\ & = \left(\frac{144}{25}\right) + 1 \\ & = \frac{144 + 25}{25} \\ & = \frac{169}{25} \end{align*}RHS
\begin{align*} {\sec}^{2}\theta & = {\left(\frac{r}{x}\right)}^{2} \\ & = {\left(\frac{13}{-5}\right)}^{2} \\ & = \frac{169}{25} \end{align*}Therefore the LHS = RHS and we have proved that \({\tan}^{2}\theta + 1 = {\sec}^{2}\theta\).
Whenever you have to solve trigonometric problems without a calculator, it can be very helpful to make a sketch.
\(B\) is a point in the Cartesian plane. Determine without using a calculator:
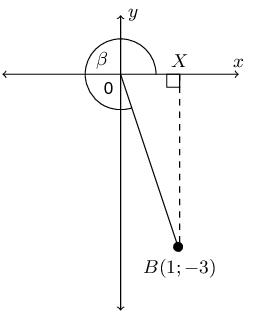
\(OB\)
\(OB\) is the hypotenuse of \(\triangle BOX\). We can calculate the length of \(OB\) using the theorem of Pythagoras:
\begin{align*} OB^{2} & = OX^{2} + XB^{2} \\ & = (1)^{2} + (3)^{2} \\ & = 10 \\ OB & = \sqrt{10} \end{align*}\(\cos \beta\)
From the diagram and the first question we know that \(x = 1\), \(y = -3\) and \(r = \sqrt{10}\).
\begin{align*} \cos \beta & = \frac{x}{r} \\ & = \frac{1}{\sqrt{10}} \end{align*}\(\text{cosec } \beta\)
From the diagram and the first question we know that \(x = 1\), \(y = -3\) and \(r = \sqrt{10}\).
\begin{align*} \text{cosec } \beta & = \frac{r}{y} \\ & = \frac{\sqrt{10}}{-3} \end{align*}\(\tan \beta\)
From the diagram and the first question we know that \(x = 1\), \(y = -3\) and \(r = \sqrt{10}\).
\begin{align*} \tan \beta & = \frac{y}{x} \\ & = \frac{-3}{1} \\ & = -3 \end{align*}If \(\sin \theta = \text{0,4}\) and \(\theta\) is an obtuse angle, determine:
\(\cos \theta\)
We first need to determine \(x\), \(y\) and \(r\).
\begin{align*} \sin \theta & = \text{0,4} \\ & = \frac{4}{10} \\ & = \frac{2}{5} \\ & = \frac{y}{r} \end{align*}Therefore \(y = 2\) and \(r = 5\).
\begin{align*} x^{2} & = r^{2} - y^{2} \\ & = (5)^{2} - (2)^{2} \\ & = 21 \\ x & = \pm \sqrt{21} \end{align*}We are told that the angle is obtuse. An obtuse angle is greater than 90° but less than 180°. Therefore the angle is in the second quadrant and \(x\) is negative. Therefore \(x = - \sqrt{21}\).
Next draw a sketch:
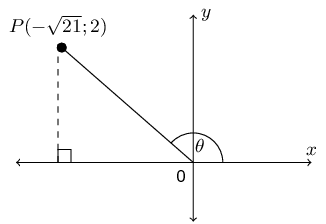
Now we can determine \(\cos \theta\):
\begin{align*} \cos \theta & = \frac{x}{r} \\ & = \frac{-\sqrt{21}}{5} \end{align*}\(\sqrt{21} \tan \theta\)
From the first question we have a sketch of the angle and \(x\), \(y\) and \(r\).
\begin{align*} \sqrt{21} \tan \theta & = \sqrt{21}\left(\frac{y}{x}\right) \\ & = \sqrt{21}\left(\frac{2}{-\sqrt{21}}\right) \\ & = -2 \end{align*}Given \(\tan \theta = \dfrac{t}{2}\), where \(0° \le \theta \le 90°\). Determine the following in terms of \(t\):
\(\sec \theta\)
We first need to determine \(x\), \(y\) and \(r\). We are given \(\tan \theta = \dfrac{t}{2}\) and so we can use this to find \(x\) and \(y\).
\begin{align*} \tan \theta & = \frac{t}{2} \\ \frac{y}{x} & = \frac{t}{2} \end{align*}Therefore \(y = t\) and \(x = 2\).
\begin{align*} r^{2} & = x^{2} + y^{2} \\ & = (2)^{2} + (t)^{2} \\ & = 4 + t^{2} \\ r & = \sqrt{4 + t^{2}} \end{align*}We are told that \(0° \le \theta \le 90°\). Therefore the angle is in the first quadrant. Even though we do not know the value of \(t\) we can draw a rough sketch:
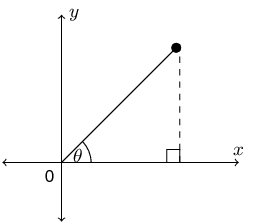
Now we can determine \(\sec \theta\):
\begin{align*} \sec \theta & = \frac{r}{x} \\ & = \frac{\sqrt{t^2 + 4}}{2} \end{align*}\(\cot \theta\)
From the first question we have a sketch of the angle and \(x\), \(y\) and \(r\).
\begin{align*} \cot \theta & = \frac{x}{y} \\ & = \frac{2}{t} \end{align*}\(\cos^{2} \theta\)
From the first question we have a sketch of the angle and \(x\), \(y\) and \(r\).
\begin{align*} \cos^2 \theta & = \left(\frac{x}{r}\right)^{2} \\ & = \left(\frac{2}{\sqrt{t^2 + 4}} \right)^2 \\ &= \frac{4}{t^2 + 4} \end{align*}\(\tan^{2} \theta - \sec^{2} \theta\)
From the first question we have a sketch of the angle and \(x\), \(y\) and \(r\).
\begin{align*} \tan^2 \theta - \sec^2 \theta & = \left(\frac{y}{x}\right)^{2} + \left(\frac{x}{y}\right)^{2} \\ & = \left(\frac{t}{2}\right)^{2} - \left(\frac{\sqrt{t^2 + 4}}{2} \right)^{2} \\ & = \frac{t^{2}}{4} - \frac{t^2 + 4}{4} \\ & =\frac{t^{2} - t^{2} - 4}{4} \\ & = -1 \end{align*}Given: \(10 \cos \beta + 8 = 0\) and \(180^{\circ} < \beta < 360^{\circ}\). Determine the value of:
\(\cos \beta\)
We are given an equation with \(\cos \beta\) in it. We can therefore rearrange this equation to find \(\cos \beta\):
\begin{align*} 10 \cos \beta + 8 & = 0 \\ \cos \beta & = \frac{-8}{10} \\ & = \frac{-4}{5} \end{align*}\(\dfrac{3}{\tan{\beta}} + 2 \sin^2{\beta}\)
We first need to determine \(x\), \(y\) and \(r\). In the first question we found that \(\cos \beta = \frac{-4}{5}\) and so we can use this to find \(x\) and \(r\).
\begin{align*} \cos \beta & = \frac{-4}{5} \\ \frac{x}{r} & = \frac{-4}{5} \end{align*}Therefore \(x = -4\) and \(r = 5\).
\begin{align*} y^{2} & = r^{2} - x^{2} \\ & = (5)^{2} - (-4)^{2} \\ & = 25 - 16 \\ y & = \pm 3 \end{align*}We are told that \(180^{\circ} < \beta < 360^{\circ}\). Therefore the angle is in the third quadrant and \(y = -3\). We can draw a rough sketch of the angle:
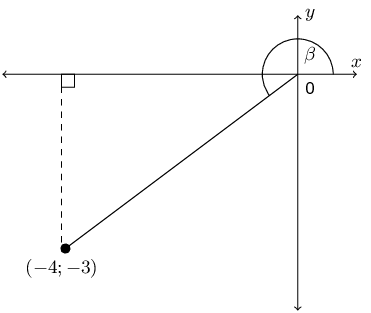
We can now find \(\frac{3}{\tan{\beta}} + 2 \sin^2{\beta}\):
\begin{align*} \frac{3}{\tan{\beta}} + 2 \sin^2{\beta} & = \frac{3}{\frac{y}{x}} + 2\left(\frac{y}{r}\right)^{2} \\ & = \frac{3x}{y} + \frac{2y^{2}}{r^{2}} \\ & = \frac{3(-4)}{-3} + \frac{2(-3)^{2}}{(5)^{2}} \\ & = \frac{-12}{3} + \frac{18}{25} \\ & = -4 + \frac{18}{25} \\ & = \frac{-100 + 18}{25} \\ & = \frac{-82}{25} \end{align*}If \(\sin{\theta} = -\dfrac{15}{17}\) and \(\cos \theta < 0\) find the following, without the use of a calculator:
We first need to determine \(x\), \(y\) and \(r\). We are given \(\sin{\theta} = -\frac{15}{17}\) and so we can use this to find \(y\) and \(r\).
\begin{align*} \sin \theta & = -\frac{15}{17} \\ \frac{y}{r} & = -\frac{15}{17} \end{align*}Therefore \(y = -15\) and \(r = 17\) (remember that \(r\) cannot be negative).
\begin{align*} x^{2} & = r^{2} - y^{2} \\ & = (17)^{2} - (-15)^{2} \\ & = 289 - 225 \\ x & = \pm 8 \end{align*}We are told that \(\cos \theta < 0\). Therefore the angle is in either the second or the third quadrant. From the value of \(y\) we see that the angle must lie in the third quadrant and \(x = -8\).
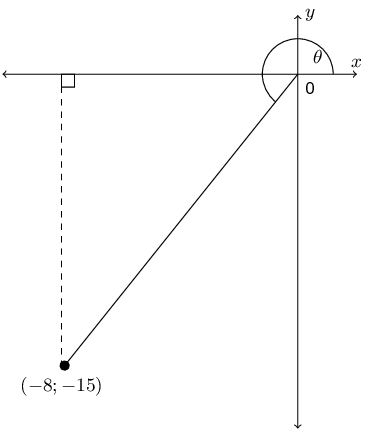
Now we can determine \(\cos \theta\):
\begin{align*} \cos \theta & = \frac{x}{r} \\ & = \frac{-8}{17} \end{align*}From the first part we have \(x = -8\), \(y = -15\) and \(r = 17\) so we can find \(\tan \theta\).
\begin{align*} \tan \theta & = \frac{y}{x} \\ & = \frac{-15}{-8} \\ & = \frac{15}{8} \end{align*}From the first part we have \(x = -8\), \(y = -15\) and \(r = 17\) so we can find \(\cos^2 \theta + \sin^2 \theta\).
\begin{align*} \cos^2 \theta + \sin^2 \theta & = \left(\frac{x}{r}\right)^{2} + \left(\frac{y}{r}\right)^{2} \\ & = \frac{x^{2}}{r^{2}} + \frac{y^{2}}{r^{2}} \\ & = \frac{x^{2} + y^{2}}{r^{2}} \\ & = \frac{(-8)^{2} + (-15)^{2}}{(17)^{2}} \\ & = \frac{64 + 225}{289} \\ & = 1 \end{align*}Find the value of \(\sin A + \cos A\) without using a calculator, given that \(13 \sin A - 12 = 0\), where \(\cos A < 0\).
We first need to determine \(x\), \(y\) and \(r\). We are given \(13 \sin A - 12 = 0\) and so we can use this to find \(y\) and \(r\).
\begin{align*} 13 \sin A - 12 & = 0 \\ \sin A & = \frac{12}{13} \end{align*}Therefore \(y = 12\) and \(r = 13\).
\begin{align*} x^{2} & = r^{2} - y^{2} \\ & = (13)^{2} - (12)^{2} \\ & = 169 - 144 \\ x & = \pm 5 \end{align*}We are told that \(\cos A < 0\). Therefore the angle is in either the second or the third quadrant. From the value of \(y\) we see that the angle must lie in the second quadrant.
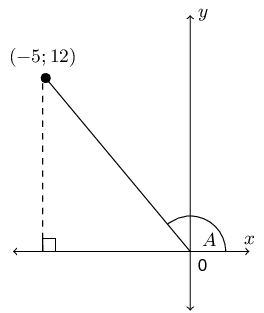
Now we can determine \(\sin A + \cos A\):
\begin{align*} \sin A + \cos A & = \frac{y}{r} + \frac{x}{r} \\ & = \frac{y + x}{r} \\ & = \frac{12 - 5}{13} \\ & = \frac{7}{13} \end{align*}If \(17 \cos \theta = -8\) and \(\tan \theta > 0\) determine the following with the aid of a diagram (not a calculator):
\(\dfrac{\cos \theta}{\sin \theta}\)
We first need to determine \(x\), \(y\) and \(r\). We are given \(17 \cos \theta = -8\) and so we can use this to find \(x\) and \(r\).
\begin{align*} 17 \cos \theta = -8 & = 0 \\ \cos \theta & = \frac{-8}{17} \end{align*}Therefore \(x = -8\) and \(r = 17\).
\begin{align*} y^{2} & = r^{2} - x^{2} \\ & = (17)^{2} - (8)^{2} \\ y & = \pm 15 \end{align*}We are told that \(\tan \theta > 0\). Therefore the angle is in either the first or the third quadrant. From the value of \(x\) we see that the angle must lie in the third quadrant.
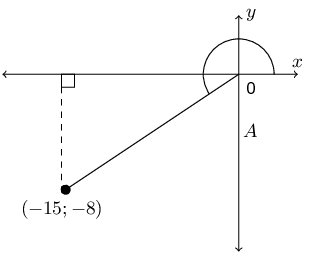
Now we can determine \(\dfrac{\cos \theta}{\sin \theta}\):
\begin{align*} \frac{\cos \theta}{\sin \theta} & = \cos \theta \times \frac{1}{\sin \theta} \\ & = \frac{y}{r} \times \frac{1}{\frac{x}{r}} \\ & = \frac{y}{r} \times \frac{r}{x} \\ & = \frac{y}{x} \\ & = \frac{-8}{-15} \\ & = \frac{8}{15} \end{align*}\(17 \sin \theta - 16 \tan \theta\)
From the first part we have that \(x = -15\), \(y = -8\) and \(r = 17\).
\begin{align*} 17 \sin \theta - 16 \tan \theta & = 17\frac{y}{r} - 16\frac{y}{x} \\ & = 17\left(\frac{-15}{17}\right) - 16\left(\frac{-15}{-8}\right) \\ & = -15 - 2(15) \\ & = -45 \end{align*}\(L\) is a point with co-ordinates \((5;8)\) on a Cartesian plane. \(LK\) forms an angle, \(\theta\), with the positive \(x\)-axis. Set up a diagram and use it to answer the following questions.
Find the distance \(LK\).
We are given \(L(5;8)\). Therefore the angle lies in the first quadrant. We can sketch this and use our sketch to find \(x\), \(y\) and \(r\).
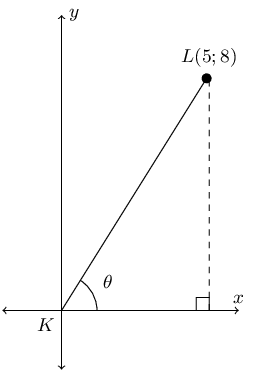
Therefore \(x = 5\) and \(y = 8\). We can calculate \(r\) using the theorem of Pythagoras. From the diagram we note that \(LK = r\).
\begin{align*} LK^{2} & = 5^{2} + 8^{2} \\ & = 89 \\ LK & = \sqrt{89} \end{align*}\(\sin \theta\)
From the previous question we have that \(x = 5\), \(y = 8\) and \(r = \sqrt{89}\).
\begin{align*} \sin \theta & = \frac{y}{r} \\ & = \frac{8}{\sqrt{89}} \end{align*}\(\cos \theta\)
From the previous question we have that \(x = 5\), \(y = 8\) and \(r = \sqrt{89}\).
\begin{align*} \cos \theta & = \frac{x}{r} \\ & = \frac{5}{\sqrt{89}} \end{align*}\(\tan \theta\)
From the previous question we have that \(x = 5\), \(y = 8\) and \(r = \sqrt{89}\).
\begin{align*} \tan \theta & = \frac{y}{x} \\ & = \frac{8}{5} \end{align*}\(\text{cosec } \theta\)
From the previous question we have that \(x = 5\), \(y = 8\) and \(r = \sqrt{89}\).
\begin{align*} \text{cosec } \theta & = \frac{r}{y} \\ & = \frac{\sqrt{89}}{8} \end{align*}\(\sec \theta\)
From the previous question we have that \(x = 5\), \(y = 8\) and \(r = \sqrt{89}\).
\begin{align*} \sec \theta & = \frac{r}{x} \\ & = \frac{\sqrt{89}}{5} \end{align*}\(\cot \theta\)
From the previous question we have that \(x = 5\), \(y = 8\) and \(r = \sqrt{89}\).
\begin{align*} \cot \theta & = \frac{x}{y} \\ & = \frac{5}{8} \end{align*}\(\sin^{2} \theta + \cos^{2} \theta\)
From the previous question we have that \(x = 5\), \(y = 8\) and \(r = \sqrt{89}\).
\begin{align*} \sin^{2} \theta + \cos^{2} \theta & = \left(\frac{y}{r}\right)^{2} + \left(\frac{x}{r}\right)^{2} \\ & = \frac{y^{2}}{r^{2}} + \frac{x^{2}}{r^{2}} \\ & = \frac{y^{2} + x^{2}}{r^{2}} \\ & = \frac{64 + 25}{89} \\ & = 1 \end{align*}Given the following diagram and that \(\cos \theta = -\frac{24}{25}\).
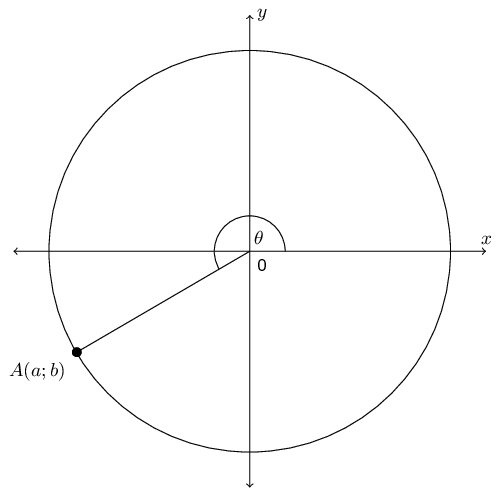
State two sets of possible values of \(a\) and \(b\).
We first need to use the given information to find a possible set of values for \(a\) and \(b\).
Using \(\cos \theta = -\frac{24}{25}\) and the fact that \(\cos \theta = \dfrac{x}{r}\) we can determine that \(x = -24\) and \(r = 25\). Now we can find \(y\):
\begin{align*} y^{2} & = r^{2} - x^{2} \\ & = (25)^2 - (24)^2 \\ & = 625 - 576 \\ & = 49 \\ y & = \pm 7 \end{align*}From the diagram we see that \(y\) must be negative.
This gives us one possible set of values for \(a\) and \(b\): \(a = 24\) and \(b = -7\).
Now we note that we can simply double the size of the circle and the trigonometric ratios will stay the same. We could even multiply the radius of the circle by any integer and the trigonometric ratios will still remain the same.
Therefore the possible sets of values for \(A(a,b)\) are multiples of \((-24;-7)\). Two possible sets are \((-24;-7)\) and \((-48;-14)\).
If \(OA = 100\), state the values of \(a\) and \(b\).
First note that in the original diagram \(OA = 25\). Now we are multiplying \(OA\) by 4. This also means that the \(x\) and \(y\) values must be multiplied by 4.
Therefore \(a = 4(-24) = -96\) and \(b = 4(-7) = -28\).
Hence determine without the use of a calculator the value of \(\sin \theta\).
The question states: “hence”. This means we must use the scaled values for \(a\) and \(b\) not the original values. We know that \(x = -96\), \(y = -28\) and \(r = 100\).
\begin{align*} \sin \theta & = \frac{y}{r} \\ &= \frac{-28}{100}\\ &= \frac{-7}{25} \end{align*}Notice how the answer reduced to the original values of \(y\) and \(r\) as we would expect from the first question.
If \(\tan{\alpha} = \dfrac{5}{-12}\) and \(0^{\circ} \le \alpha \le 180^{\circ}\), determine without the use of a calculator the value of \(\dfrac{12}{\cos{\alpha}}\)
We first need to determine \(x\), \(y\) and \(r\). We are given \(\tan \alpha = \dfrac{5}{-12}\) and so we can use this to find \(x\) and \(y\).
\begin{align*} \tan \alpha & = \frac{5}{-12} \\ \frac{y}{x} & = \frac{5}{-12} \end{align*}Therefore \(y = 5\) and \(x = -12\).
\begin{align*} r^{2} & = x^{2} + y^{2} \\ & = (-12)^{2} + (5)^{2} \\ & = 144 + 25 \\ r & = 13 \end{align*}We are told that \(0° \le \alpha \le 180°\). Therefore the angle is in either the first or the second quadrant. From the values of \(x\) and \(y\) we see that the angle must lie in the second quadrant.
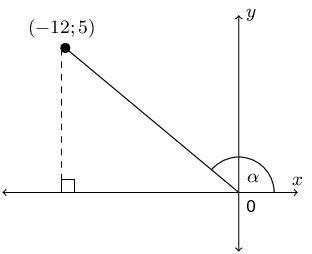
Now we can determine \(\dfrac{12}{\cos{\alpha}}\):
\begin{align*} \frac{12}{\cos{\alpha}} & = \frac{12}{\frac{x}{r}} \\ & = \frac{12r}{x} \\ & = \frac{12(13)}{-12} \\ & = -13 \end{align*}|
Previous
5.7 Solving trigonometric equations
|
Table of Contents |
Next
5.9 Chapter summary
|