through points \(\left(-1;3\right)\) and \(\left(1;4\right)\)
End of chapter exercises
|
Previous
4.6 Summary
|
Next
5.1 Quadratic functions
|
End of chapter exercises
Determine the equation of the line:
through points \(\left(7;-3\right)\) and \(\left(0;4\right)\)
parallel to \(y=\frac{1}{2}x+3\) and passing through \(\left(-2;3\right)\)
perpendicular to \(y=-\frac{1}{2}x+3\) and passing through \(\left(-1;2 \right)\)
perpendicular to \(3y+x=6\) and passing through the origin
Determine the angle of inclination of the following lines:
\(y=2x-3\)
\(y=\frac{1}{3}x-7\)
\(4y=3x+8\)
\(y=-\frac{2}{3}x+3\)
\(3y+x-3=0\)
\(P(2;3)\), \(Q(-4;0)\) and \(R(5;-3)\) are the vertices of \(\triangle PQR\) in the Cartesian plane. \(PR\) intersects the \(x\)-axis at \(S\). Determine the following:
the equation of the line \(PR\)
the coordinates of point \(S\)
the angle of inclination of \(PR\) (correct to two decimal places)
the gradient of line \(PQ\)
\(Q\hat{P}R\)
the equation of the line perpendicular to \(PQ\) and passing through the origin
the mid-point \(M\) of \(QR\)
the equation of the line parallel to \(PR\) and passing through point \(M\)
Points \(A(-3;5)\), \(B(-7;-4)\) and \(C(2;0)\) are given.
Plot the points on the Cartesian plane.
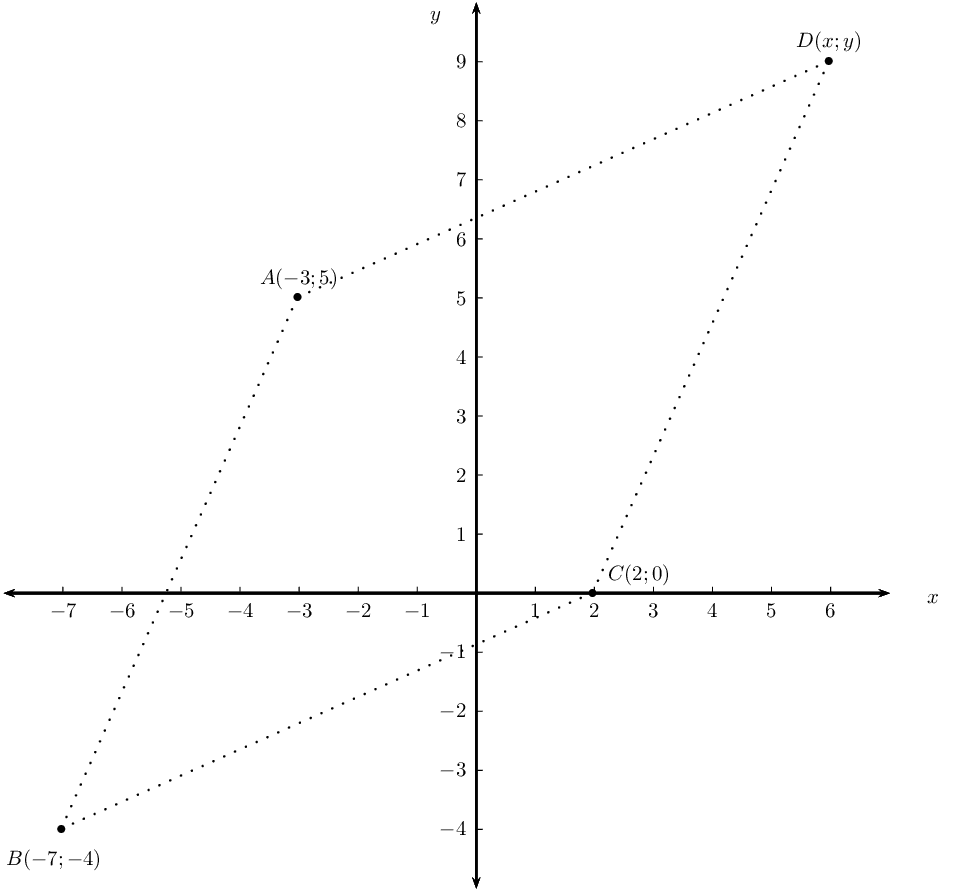
Determine the coordinates of \(D\) if \(ABCD\) is a parallelogram.
Prove that \(ABCD\) is a rhombus.
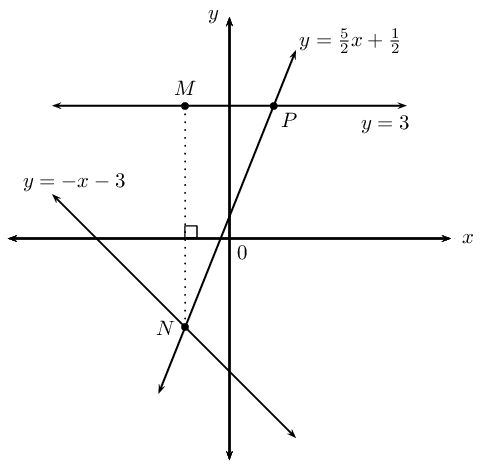
Consider the sketch above, with the following lines shown:
\(y = -x -3\)
\(y = 3\)
\(y = \frac{5}{2}x + \frac{1}{2}\)
Determine the coordinates of the point \(N\).
Determine the coordinates of the point \(P\).
Determine the equation of the vertical line \(MN\).
Determine the length of the vertical line \(MN\).
Find \(M\hat{N}P\).
Determine the equation of the line parallel to \(NP\) and passing through the point \(M\).
The following points are given: \(A(-2;3)\), \(B(2;4)\), \(C(3;0)\).
Plot the points on the Cartesian plane.
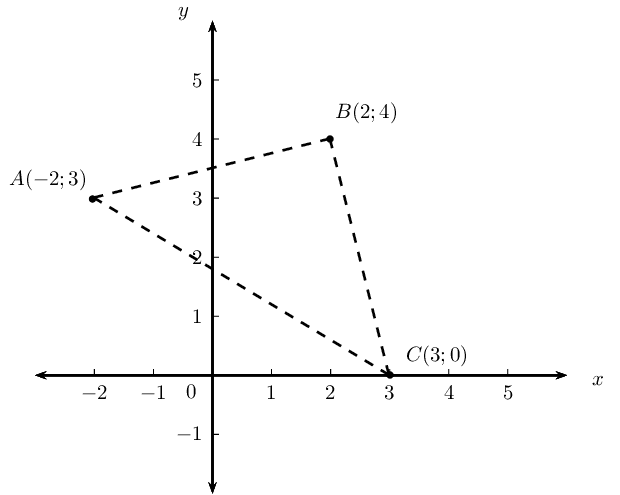
Prove that \(\triangle ABC\) is a right-angled isosceles triangle.
Determine the equation of the line \(AB\).
Determine the coordinates of \(D\) if \(ABCD\) is a square.
Determine the coordinates of \(E\), the mid-point of \(BC\).
Given points \(S(2;5)\), \(T(-3;-4)\) and \(V(4;-2)\).
Determine the equation of the line \(ST\).
Determine the size of \(T\hat{S}V\).
Consider triangle \(FGH\) with vertices \(F(-1;3)\), \(G(2;1)\) and \(H(4;4)\).
Sketch \(\triangle FGH\) on the Cartesian plane.
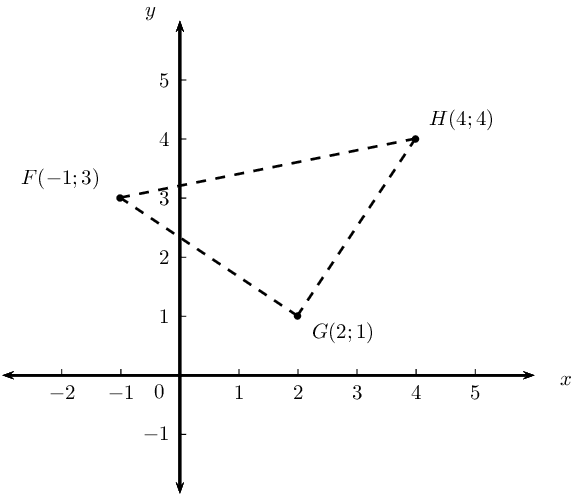
Show that \(\triangle FGH\) is an isosceles triangle.
Determine the equation of the line \(PQ\), perpendicular bisector of \(FH\).
Does \(G\) lie on the line \(PQ\)?
Determine the equation of the line parallel to \(GH\) and passing through point \(F\).
Given the points \(A(-1;5)\), \(B(5;-3)\) and \(C(0;-6)\). \(M\) is the mid-point of \(AB\) and \(N\) is the mid-point of \(AC\).
Draw a sketch on the Cartesian plane.
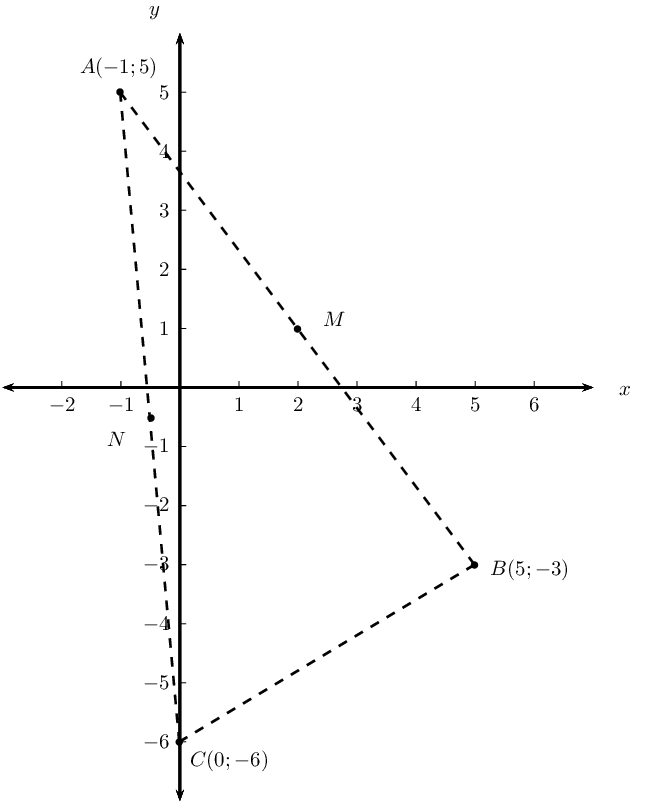
Show that the coordinates of \(M\) and \(N\) are \((2;1)\) and \((-\frac{1}{2};-\frac{1}{2})\) respectively.
Use analytical geometry methods to prove the mid-point theorem. (Prove that \(NM \parallel CB\) and \(NM = \frac{1}{2}CB\).)
|
Previous
4.6 Summary
|
Table of Contents |
Next
5.1 Quadratic functions
|
