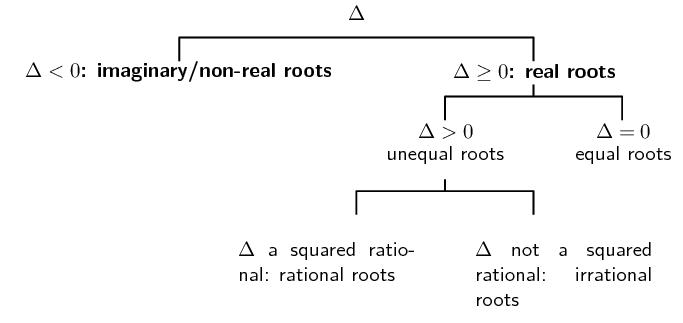
Show that \({k}^{2}{x}^{2}+2=kx-{x}^{2}\) has non-real roots for all
real values for \(k\).
[IEB, Nov. 2002, HG]
\begin{align*}
k^2 x^2 + x^2 - kx +2 &= 0\\
a &= (k^2+1)\\
b&= -k\\
c&=2\\
\Delta &= b^2-4ac\\
&= (-k)^2 - 4(k^2+1)(2)\\
&=k^2-8k^2-8\\
&=-7k^2 - 8\\
&=-(7k^2 + 8)\\
\Delta & < 0
\end{align*}Therefore the roots are non-real.
If \(b\) and \(c\) can take on only the values \(\text{1}\),
\(\text{2}\) or \(\text{3}\), determine all pairs (\(b; c\))
such that \({x}^{2}+bx+c=0\) has real roots.
[IEB, Nov. 2005, HG]
We need to find the values of \(a\), \(b\) and \(c\) for which
\(\Delta \geq 0\).
\begin{align*}
a&=1\\
b&=\text{1,2} \text{ or }3\\
c&=\text{1,2} \text{ or }3\\
\\
\Delta &= b^2-4ac\\
&= b^2 - 4(1)c
\end{align*}
Possible pair values of \((b;c)\):
\((1;1),~(1;2),~(1;3),~(2;1),~(2;2),~(2;3),~(3;1),~(3;2),~(3;3)\).
Corresponding values of \(\Delta\): \((\Delta < 0),~(\Delta
< 0),~(\Delta < 0),~(\Delta = 0),~(\Delta < 0),~(\Delta
< 0),~(\Delta >0),~(\Delta > 0),~(\Delta < 0)\)
\(\Delta ≥ 0\) (and therefore the roots are real) for \((b;c) =
(2;1),~(3;1),~(3;2)\)