Mr. Tsilatsila builds a fence around his rectangular vegetable garden of \(\text{8}\)
\(\text{m$^{2}$}\). If the length is twice the breadth, determine the dimensions of Mr.
Tsilatsila's vegetable garden.
We let the length be \(l\) and the breadth be \(b\). The area of the garden is \(\text{8}\)
\(\text{m$^{2}$}\) and is given by \(A = l \times b\).
Since the length is twice the breadth we can express the length in terms of the breadth: \(l
= 2b\). We now have the following:
\begin{align*}
A = 8 & = l \times b \\
& = 2b(b) \\
& = 2b^{2} \\
b^{2} & = 4 \\
b & = \pm 2
\end{align*}
Therefore the breadth is \(\text{2}\) \(\text{m}\) and the length is twice this, \(\text{4}\)
\(\text{m}\). Note that the breadth cannot be a negative number and so we do not consider
this solution.
Kevin has played a few games of ten-pin bowling. In the third game, Kevin scored
\(\text{80}\) more than in the second game. In the first game Kevin scored \(\text{110}\)
less than the third game. His total score for the first two games was \(\text{208}\). If he
wants an average score of \(\text{146}\), what must he score on the fourth game?
We let the score for the first game be \(a\), the score for the second game be \(b\), the
score for the third game be \(c\) and the score for the fourth game be \(d\).
Now we note the following:
\begin{align*}
c & = 80 + b \\
a & = c - 110 \\
a + b & = 208 \\
\frac{a + b + c + d}{4} & = 146
\end{align*}
We make the \(c\) the subject of the first two equations:
\begin{align*}
c & = 80 + b \\
c & = a + 110
\end{align*}
And then we use \(a = 208 - b\) to solve for \(b\):
\begin{align*}
80 + b & = 208 - b + 110 \\
2b & = 208 + 110 - 80 \\
2b & = 238 \\
b & = 119
\end{align*}
Now we can find \(a\):
\begin{align*}
a + b & = 208 \\
a + 119 & = 208 \\
a & = 89
\end{align*}
And we can find \(c\):
\begin{align*}
c & = 80 + b \\
c & = 80 + 208 \\
c & = 288
\end{align*}
Finally we can find \(d\):
\begin{align*}
\frac{a + b + c + d}{4} & = 164 \\
496 + d & = 656 \\
d & = 187
\end{align*}
Kevin must score \(\text{187}\) in the fourth game.
When an object is dropped or thrown downward, the distance, \(d\), that it falls in time,
\(t\), is described by the following equation:
\(s=5{t}^{2}+{v}_{0}t\)
In this equation, \({v}_{0}\) is the initial velocity, in \(\text{m·s$^{-1}$}\).
Distance is measured in meters and time is measured in seconds. Use the equation to find how
long it takes a tennis ball to reach the ground if it is thrown downward from a hot-air
balloon that is \(\text{500}\) \(\text{m}\) high. The tennis ball is thrown at an initial
velocity of \(\text{5}\) \(\text{m·s$^{-1}$}\).
We are given the distance that the ball falls and the initial velocity so we can solve for
\(t\):
\begin{align*}
s & = 5{t}^{2} + {v}_{0}t \\
500 & = 5t^{2} + 5t \\
0 &= 5t^{2} + 5t - 500 \\
0 &= t^{2} + t - 100
\end{align*}
\begin{align*}
t &= \dfrac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \\
\therefore t & = \dfrac{-(1) \pm \sqrt{(1)^{2} - 4(1)(-100)}}{2(1)} \\
& = \dfrac{-1 \pm \sqrt{1 + 400}}{2} \\
& = \dfrac{-1 \pm \sqrt{401}}{2}
\end{align*}
Since time cannot be negative the only solution is \(t = \dfrac{-1 + \sqrt{401}}{2} \approx
\text{9,5}\text{ s}\).
The table below lists the times that Sheila takes to walk the given distances.
|
time (minutes)
|
\(\text{5}\)
|
\(\text{10}\)
|
\(\text{15}\)
|
\(\text{20}\)
|
\(\text{25}\)
|
\(\text{30}\)
|
|
distance (km)
|
\(\text{1}\)
|
\(\text{2}\)
|
\(\text{3}\)
|
\(\text{4}\)
|
\(\text{5}\)
|
\(\text{6}\)
|
Plot the points.
Find the equation that describes the relationship between time and distance. Then use the
equation to answer the following questions:
-
How long will it take Sheila to walk \(\text{21}\) \(\text{km}\)?
-
How far will Sheila walk in \(\text{7}\) minutes?
If Sheila were to walk half as fast as she is currently walking, what would the graph of her
distances and times look like?
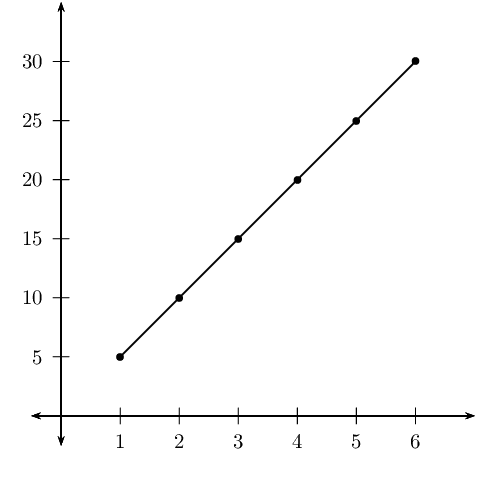
The equation is \(t = 5d\).
It will take Sheila \(t = 5(21) = 105\) minutes to walk \(\text{21}\) \(\text{km}\).
Sheila will walk \(d = \frac{7}{5} = \text{1,4}\) kilometres in \(\text{7}\) minutes.
The gradient of the graph will be twice the gradient of the first graph. The graph will be
steeper and lie closer to the \(y\)-axis.
The power \(P\) (in watts) supplied to a circuit by a \(\text{12}\) volt battery is given by
the formula \(P = 12I - \text{0,5}I^2\) where \(I\) is the current in amperes.
-
Since both power and current must be greater than \(\text{0}\), find the limits of
the current that can be drawn by the circuit.
-
Draw a graph of \(P = 12I - \text{0,5}I^2\) and use your answer to the first question
to define the extent of the graph.
-
What is the maximum current that can be drawn?
-
From your graph, read off how much power is supplied to the circuit when the current
is \(\text{10}\) A. Use the equation to confirm your answer.
-
At what value of current will the power supplied be a maximum?
-
We set the equation equal to \(\text{0}\) to find the limits:
\begin{align*}
0 & = 12I - \text{0,5}I^{2} \\
\text{0,5}I^{2} - 12I & = 0 \\
I(\text{0,5}I - 12) & = 0 \\
I = 0 & \text{ or } I = 24
\end{align*}
-
-
The maximum current that can be drawn is \(\text{24}\) \(\text{A}\).
-
The power is \(\text{70}\) \(\text{W}\).
\begin{align*}
P & = 12(10) - \frac{1}{2}(10)^{2} \\
& = 120 - 50 \\
& = 70
\end{align*}
-
\(\text{12}\) \(\text{A}\). This is the turning point of the parabola.
A wooden block is made as shown in the diagram. The ends are right-angled triangles having
sides \(3x\), \(4x\) and \(5x\). The length of the block is \(y\). The total surface area of
the block is \(\text{3 600}\) \(\text{cm$^{2}$}\).
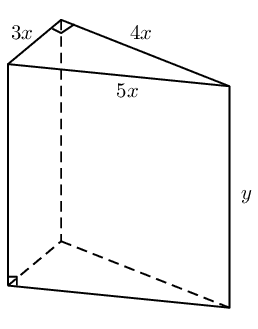
Show that
\(y=\frac{300-{x}^{2}}{x}\)
\begin{align*}
\text{3 600} & = 3xy + 5xy + 4xy + 2 \left( \frac{1}{2}(3x)(4x) \right) \\
\text{3 600} & = 12xy + 12x^2 \\
\text{3 600} - 12x^2 & = 12xy \\
\frac{\text{3 600} - 12x^2}{12x} & = y \\
\therefore y & = \frac{\text{300} - x^2}{x}
\end{align*}


