8.3 Summary

• If \(O\) is the centre and \(OM \perp AB\), then \(AM = MB\).
• If \(O\) is the centre and \(AM = MB\), then \(A\hat{M}O = B\hat{M}O = \text{90}\text{°}\).
• If \(AM = MB\) and \(OM \perp AB\), then \(\Rightarrow MO\) passes through centre \(O\).

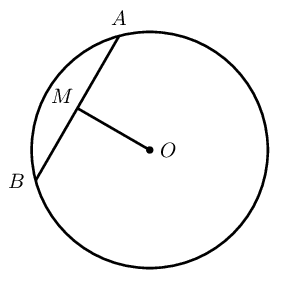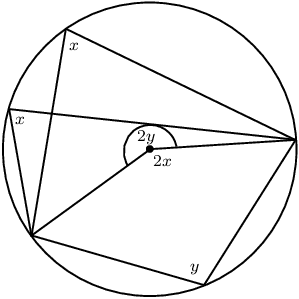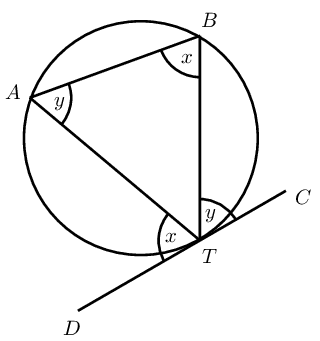
If an arc subtends an angle at the centre of a circle and at the circumference, then the angle at the centre is twice the size of the angle at the circumference.

Angles at the circumference subtended by the same arc (or arcs of equal length) are equal.

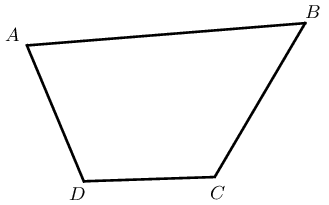
The four sides of a cyclic quadrilateral \(ABCD\) are chords of the circle with centre \(O\).

• \(\hat{A} + \hat{C} = \text{180}\text{°}\) (opp. \(\angle\)s supp.)
• \(\hat{B} + \hat{D} = \text{180}\text{°}\) (opp. \(\angle\)s supp.)
• \(E\hat{B}C = \hat{D}\) (ext. \(\angle\) cyclic quad.)
• \(\hat{A}_1 = \hat{A}_2 = \hat{C}\) (vert. opp. \(\angle\), ext. \(\angle\) cyclic quad.)

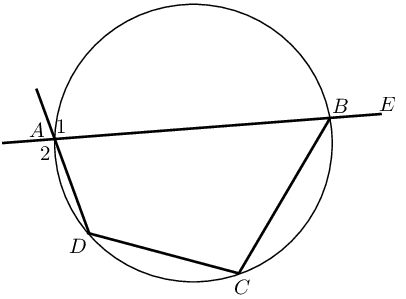
Proving a quadrilateral is cyclic: If \(\hat{A} + \hat{C} = \text{180}\text{°}\) or \(\hat{B} + \hat{D} = \text{180}\text{°}\), then \(ABCD\) is a cyclic quadrilateral.

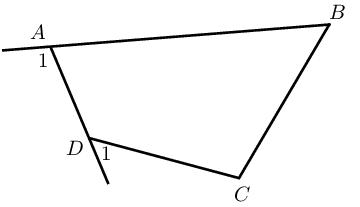If \(\hat{A}_1 = \hat{C}\) or \(\hat{D}_1 = \hat{B}\), then \(ABCD\) is a cyclic quadrilateral.

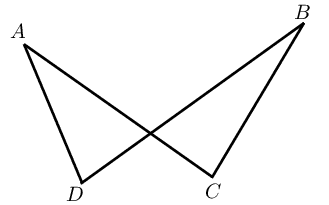If \(\hat{A} = \hat{B}\) or \(\hat{C} = \hat{D}\), then \(ABCD\) is a cyclic quadrilateral.

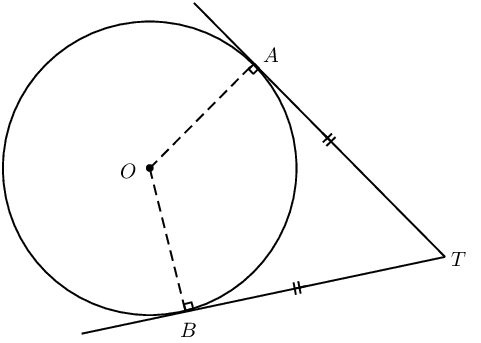If \(AT\) and \(BT\) are tangents to circle \(O\), then

• \(OA \perp AT\) (tangent \(\perp\) radius)
• \(OB \perp BT\) (tangent \(\perp\) radius)
• \(TA = TB\) (tangents from same point equal)

• If \(DC\) is a tangent, then \(D\hat{T}A = T\hat{B}A\) and \(C\hat{T}B = T\hat{A}B\)
• If \(D\hat{T}A = T\hat{B}A\) or \(C\hat{T}B = T\hat{A}B\), then \(DC\) is a tangent touching at \(T\)