Chapter 1: Exponents and surds

1.1 Revision (EMBF2)

The number system (EMBF3)

Discuss the number system; explain the difference between real and non-real numbers.
Encourage learners not to use calculators in this chapter.
Common misconception: \(\pi\) (irrational) ≈ \(\frac{22}{7}\) (rational).
Explain that the square root of a negative number is non-real.
Discuss raising a negative number to even and odd powers.
Explain that surds are a special notation or way of expressing rational exponents.
Key strategy in manipulation of exponential expressions: express base in terms of its prime factors.
Emphasize the principle of equivalence and using the additive inverse in the simplification of equations (and not “simply taking term to the other side”).
Rationalising the denominators is a useful tool for working with special angles in Trigonometry.
Learners should leave their final answers as mixed fractions.
Answers should always be written with positive exponents.

The diagram below shows the structure of the number system:

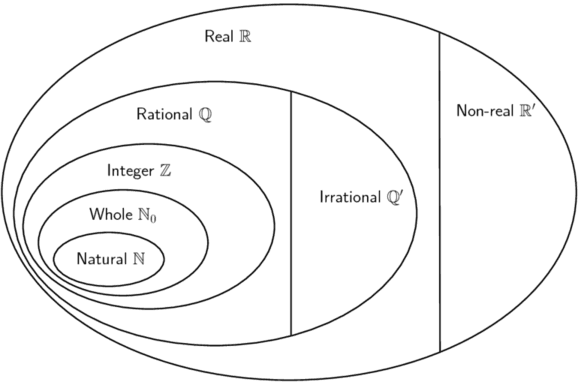
We use the following definitions:

\(\mathbb{N}\): natural numbers are \(\{1; \; 2; \; 3; \; \ldots\}\)
\(\mathbb{N}_0\): whole numbers are \(\{0; \; 1; \; 2; \; 3; \; \ldots\}\)
\(\mathbb{Z}\): integers are \(\{\ldots; \; -3; \; -2; \; -1; \; 0; \; 1; \; 2; \; 3; \; \ldots\}\)
\(\mathbb{Q}\): rational numbers are numbers which can be written as \(\frac{a}{b}\) where \(a\) and \(b\) are integers and \(b\ne 0\), or as a terminating or recurring decimal number.

Examples: \(-\frac{7}{2}; \; -\text{2,25}; \; 0; \; \sqrt{9}; \; \text{0,}\dot{8}; \; \frac{23}{1}\)
\(\mathbb{Q}'\): irrational numbers are numbers that cannot be written as a fraction with the numerator and denominator as integers. Irrational numbers also include decimal numbers that neither terminate nor recur.

Examples: \(\sqrt{3}; \; \sqrt[5]{2}; \; \pi; \; \frac{1 + \sqrt{5}}{2}; \; \text{1,27548}\ldots\)
\(\mathbb{R}\): real numbers include all rational and irrational numbers.
\(\mathbb{R}'\): non-real numbers or imaginary numbers are numbers that are not real.

Examples: \(\sqrt{-25}; \; \sqrt[4]{-1}; \; -\sqrt{-\frac{1}{16}}\)

temp text

The number system

Textbook Exercise 1.1

Use the list of words below to describe each of the following numbers (in some cases multiple words will be applicable):

Natural (\(\mathbb{N}\))
Whole (\(\mathbb{N}_0\))
Integer (\(\mathbb{Z}\))
Rational (\(\mathbb{Q}\))
Irrational (\(\mathbb{Q}'\))
Real (\(\mathbb{R}\))
Non-real (\(\mathbb{R}'\))

\(\sqrt{7}\)

\(\mathbb{R}; \mathbb{Q}'\)

\(\text{0,01}\)

\(\mathbb{R}; \mathbb{Q}\)

\(16\frac{2}{5}\)

\(\mathbb{R}; \mathbb{Q}\)

\(\sqrt{6\frac{1}{4}}\)

\(\mathbb{R}; \mathbb{Q}\)

\(\text{0}\)

\(\mathbb{R}; \mathbb{Q}; \mathbb{Z}; \mathbb{N}_0\)

\(2\pi\)

\(\mathbb{R}' \mathbb{Q}'\)

\(-\text{5,3}\dot{8}\)

\(\mathbb{R}; \mathbb{Q}\)

\(\frac{1-\sqrt{2}}{2}\)

\(\mathbb{R}; \mathbb{Q}'\)

\(-\sqrt{-3}\)

\(\mathbb{R}'\)

\((\pi)^2\)

\(\mathbb{R}; \mathbb{Q}'\)

\(-\frac{9}{11}\)

\(\mathbb{R}; \mathbb{Q}\)

\(\sqrt[3]{-8}\)

\(\mathbb{R}; \mathbb{Q}; \mathbb{Z}\)

\(\frac{22}{7}\)

\(\mathbb{R}; \mathbb{Q}\)

\(\text{2,45897}\ldots\)

\(\mathbb{R}; \mathbb{Q}'\)

\(\text{0,}\overline{65}\)

\(\mathbb{R}; \mathbb{Q}\)

\(\sqrt[5]{-32}\)

\(\mathbb{R}; \mathbb{Q}; \mathbb{Z}\)

Laws of exponents (EMBF4)

We use exponential notation to show that a number or variable is multiplied by itself a certain number of times. The exponent, also called the index or power, indicates the number of times the multiplication is repeated.

\[a^n = a \times a \times a \times \ldots \times a \quad (n \text{ times}) \qquad \left(a \in \mathbb{R}, n \in \mathbb{N}\right)\]

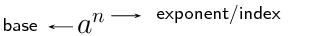
Examples:

\(2 \times 2 \times 2 \times 2 = 2^4\)
\(\text{0,71} \times \text{0,71} \times \text{0,71} = (\text{0,71})^3\)
\((\text{501})^2 = \text{501} \times \text{501}\)
\(k^6 = k \times k \times k \times k \times k \times k\)

For \(x^2\), we say \(x\) is squared and for \(y^3\), we say that \(y\) is cubed. In the last example we have \(k^6\); we say that \(k\) is raised to the sixth power.

We also have the following definitions for exponents. It is important to remember that we always write the final answer with a positive exponent.

\({a}^{0}=1\) (\(a \ne 0\) because \(0^0\) is undefined)
\({a}^{-n}=\frac{1}{{a}^{n}}\) (\(a \ne 0\) because \(\frac{1}{0}\) is undefined)

Examples:

\(5^{-2} = \dfrac{1}{5^2} = \dfrac{1}{25}\)
\((-36)^0 x = (1)x = x\)
\(\dfrac{7p^{-1}}{q^{3}t^{-2}} = \dfrac{7t^2}{pq^3}\)

We use the following laws for working with exponents:

\({a}^{m} \times {a}^{n}={a}^{m+n}\)
\(\frac{{a}^{m}}{{a}^{n}}={a}^{m-n}\)
\({\left(ab\right)}^{n}={a}^{n}{b}^{n}\)
\({\left(\frac{a}{b}\right)}^{n}=\frac{{a}^{n}}{{b}^{n}}\)
\({\left({a}^{m}\right)}^{n}={a}^{mn}\)

where \(a > 0\), \(b > 0\) and \(m, n \in \mathbb{Z}\).

Worked example 1: Laws of exponents

Simplify the following:

\(5(m^{2t})^p \times 2(m^{3p})^t\)
\(\dfrac{8k^3x^2}{(xk)^2}\)
\(\dfrac{2^2 \times 3 \times 7^4}{(7 \times 2)^4}\)
\(3(3^b)^a\)

\(5(m^{2t})^p \times 2(m^{3p})^t = 10m^{2pt + 3pt} = 10m^{5pt}\)
\(\dfrac{8k^3x^2}{(xk)^2} = \dfrac{8k^3x^2}{x^2k^2} = 8k^{(3-2)}x^{(2-2)} = 8k^1x^0 = 8k\)
\(\dfrac{2^2 \times 3 \times 7^4}{(7 \times 2)^4} = \dfrac{2^2 \times 3 \times 7^4}{7^4 \times 2^4} = 2^{(2-4)} \times 3 \times 7^{(4-4)} = 2^{-2} \times 3 = \frac{3}{4}\)
\(3(3^b)^a = 3 \times 3^{ab} = 3^{ab + 1}\)

temp text

Worked example 2: Laws of exponents

Simplify:\(\dfrac{3^m - 3^{m+1}}{4 \times 3^m - 3^m}\)

Simplify to a form that can be factorised

\[\dfrac{3^m - 3^{m+1}}{4 \times 3^m - 3^m} = \dfrac{3^m - (3^{m} \times 3)}{4 \times 3^m - 3^m}\]

Take out a common factor

\[\begin{align*} &= \dfrac{3^m(1 - 3)}{3^m(4 - 1)} \end{align*}\]

Cancel the common factor and simplify

\[\begin{align*} &= \frac{1 - 3}{4 - 1} \\ &= - \frac{2}{3} \end{align*}\]

temp text

Laws of exponents

Textbook Exercise 1.2

\(4 \times 4^{2a} \times 4^2 \times 4^a\)

\begin{align*} 4 \times 4^{2a} \times 4^2 \times 4^a &= 4^{1+2a+2+a} \\ &= 4^{3a+3} \end{align*}

\(\dfrac{3^2}{2^{-3}}\)

\begin{align*} \dfrac{3^2}{2^{-3}} &= 3^2 \times 2^3 \\ &= 9 \times 8 \\ &= 72 \end{align*}

\((3p^5)^2\)

\begin{align*} (3p^5)^2 &= 3^2 \times p^{10} \\ &= 9 p^{10} \end{align*}

\(\dfrac{k^2k^{3x-4}}{k^x}\)

\begin{align*} \dfrac{k^2k^{3x-4}}{k^x} &= \dfrac{k^{3x-2}}{k^x} \\ &= k^{3x-2-(x)} \\ &= k^{2x-2} \end{align*}

\((5^{z-1})^2+5^z\)

\[(5^{z-1})^2+5^z = 5^{2z-2}+5^z\]

\((\frac{1}{4})^0\)

\[\left ( \frac{1}{4} \right )^0 = 1\]

\((x^2)^5\)

\[\left ( x^2 \right )^5 = x^{10}\]

\(\left( \frac{a}{b} \right)^{-2}\)

\begin{align*} \left ( \frac{a}{b} \right )^{-2} &= \frac{a^{-2}}{b^{-2}} \\ &= \frac{b^2}{a^2} \end{align*}

\((m+n)^{-1}\)

\[\left ( m+n \right )^{-1} = \frac{1}{m+n}\]

\(2(p^t)^s\)

\[2\left ( p^t \right )^s = 2p^{ts}\]

\(\dfrac{1}{\left(\frac{1}{a}\right)^{-1}}\)

\[\dfrac{1}{\left ( \frac{1}{a} \right )^{-1}} = \dfrac{1}{a}\]

\(\frac{k^{0}}{k^{-1}}\)

\[\frac{k^{0}}{k^{-1}} = k\]

\(\dfrac{-2}{-2^{-a}}\)

\begin{align*} \dfrac{-2}{-2^{-a}} &= 2 \times 2^a \\ &= 2^{a+1} \end{align*}

\(\dfrac{-h}{(-h)^{-3}}\)

\begin{align*} \frac{-h}{\left ( -h \right )^{-3}} &= -h\left ( -h \right )^3 \\ &= -h\left ( -h^3 \right ) \\ &= h^4 \end{align*}

\(\left( \dfrac{a^2b^3}{c^3d} \right)^2\)

\[\left ( \frac{a^2b^3}{c^3d} \right )^2 = \frac{a^4b^6}{c^6d^2}\]

\(10^{7}(7^{0}) \times 10^{-6}(-6)^{0}-6\)

\begin{align*} 10^{7}\left ( 7^{0} \right ) \times 10^{-6}\left ( -6 \right )^{0}-6 &= 10^7(1) \times 10^{-6}(1) - 6 \\ &= 10^1 - 6 \\ &= 4 \end{align*}

\(m^3n^2 \div nm^2 \times \frac{mn}{2}\)

\begin{align*} m^3n^2 \div nm^2 \times \frac{mn}{2} &= m^3n^2 \times \frac{1}{m^2n} \times \frac{mn}{2} \\ &= \frac{m^3n^2}{m^2n} \times \frac{mn}{2} \\ &= \frac{m^2n^2}{2} \end{align*}

\((2^{-2}-5^{-1})^{-2}\)

\begin{align*} \left ( 2^{-2}-5^{-1} \right )^{-2} &= \left ( \frac{1}{4} - \frac{1}{5} \right )^{-2} \\ &= \left ( \frac{1}{20} \right )^{-2} \\ &= 20^2 \\ &= \text{400} \end{align*}

\((y^2)^{-3} \div \left( \frac{x^2}{y^3} \right)^{-1}\)

\begin{align*} \left ( y^2 \right )^{-3} \div \left ( \frac{x^2}{y^3} \right )^{-1}\div \frac{y^{-2}}{x^{-2}} &= \frac{1}{y^6} \times \frac{x^2}{y^3} \times \frac{y^{2}}{x^{2}} \\ &= \frac{1}{y^7} \end{align*}

\(\dfrac{2^{c-5}}{2^{c-8}}\)

\begin{align*} \dfrac{2^{c-5}}{2^{c-8}} &= 2^{(c-5)-(c-8)} \\ &= 2^{c-5-c+8} \\ &= 2^{3} \\ &= 8 \end{align*}

\(\dfrac{2^{9a} \times 4^{6a} \times 2^2}{8^{5a}}\)

\begin{align*} \dfrac{2^{9a} \times 4^{6a} \times 2^2}{8^{5a}} &= \frac{2^{9a} \times 2^{12a} \times 2^2}{2^{15a}} \\ &= \frac{2^{9a+12a+2}}{2^{15a}} \\ &= 2^{21a+2-15a} \\ &= 2^{6a+2} \end{align*}

\(\dfrac{20t^5p^{10}}{10t^4p^9}\)

\begin{align*} \dfrac{20t^5p^{10}}{10t^4p^9} &= 2t^{5-4}p^{10-9} \\ &= 2pt \end{align*}

\(\left( \dfrac{9q^{-2s}}{q^{-3s}y^{-4a-1}} \right)^2\)

\begin{align*} \left( \dfrac{9q^{-2s}}{q^{-3s}y^{-4a-1}} \right)^2 &= \frac{\left( 9q^{-2s} \right)^2}{\left( q^{-3s}y^{-4a-1} \right)^2} \\ &= \frac{ 81q^{-4s} }{ q^{-6s}y^{-8a-2} } \\ &= \frac{ 81q^{6s} }{ q^{4s}y^{-(8a+2)} } \\ &= 81q^{2s} y^{8a+2} \end{align*}

Table of Contents

1.2 Rational exponents and surds