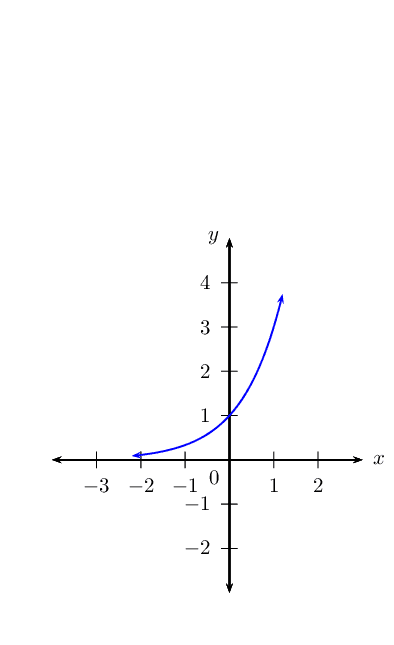
\(y_1 = 3^x\)
|
Previous
5.3 Hyperbolic functions
|
Next
5.5 The sine function
|
Functions of the general form \(y=a{b}^{x}+q\), for \(b>0\), are called exponential functions, where \(a\), \(b\) and \(q\) are constants.
The effects of \(a\), \(b\) and \(q\) on \(f(x) = ab^x + q\):
The effect of \(q\) on vertical shift
For \(q>0\), \(f(x)\) is shifted vertically upwards by \(q\) units.
For \(q<0\), \(f(x)\) is shifted vertically downwards by \(q\) units.
The horizontal asymptote is the line \(y = q\).
The effect of \(a\) on shape
For \(a>0\), \(f(x)\) is increasing.
For \(a<0\), \(f(x)\) is decreasing. The graph is reflected about the horizontal asymptote.
The effect of \(b\) on direction
Assuming \(a > 0\):
|
\(b>1\) |
\(a<0\) |
\(a>0\) |
|
\(q>0\) |
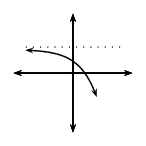 |
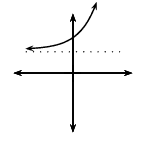 |
|
\(q<0\) |
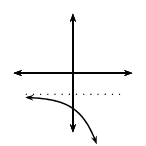 |
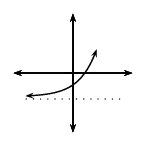 |
|
\(0<b<1\) |
\(a<0\) |
\(a>0\) |
|
\(q>0\) |
 |
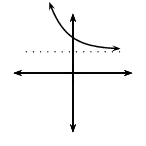 |
|
\(q<0\) |
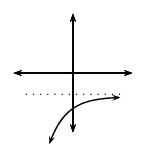 |
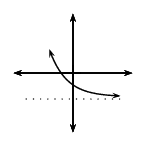 |
On separate axes, accurately draw each of the following functions:
\(y_1 = 3^x\)

\(y_2 = -2 \times 3^x\)
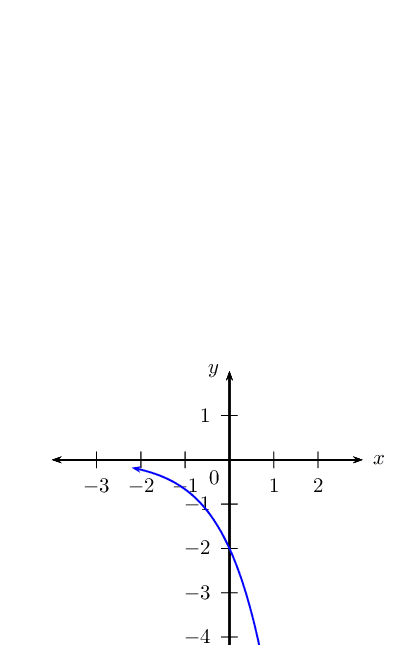
\(y_3 = 2 \times 3^x + 1\)
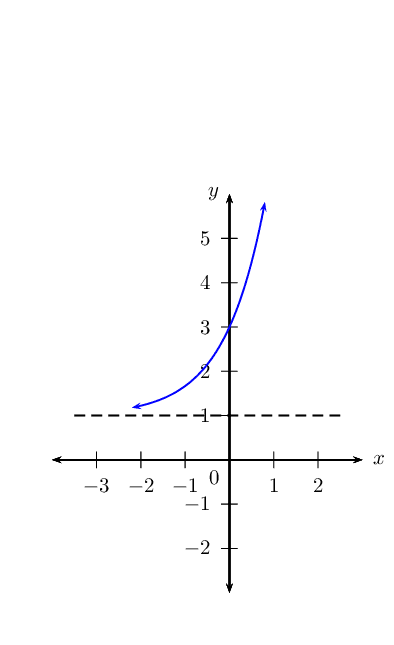
\(y_4 = 3^x - 2\)
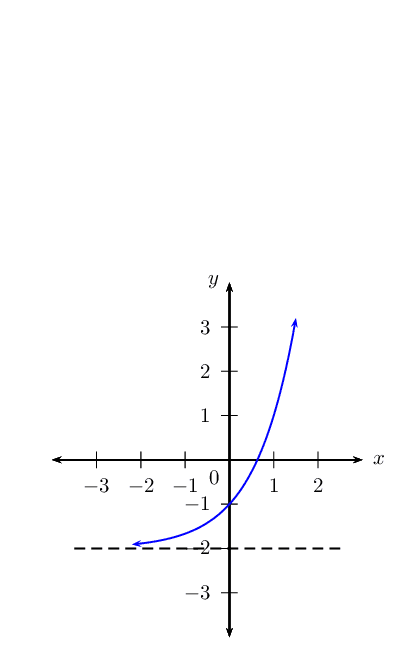
Use your sketches of the functions given above to complete the following table (the first column has been completed as an example):
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | |
| value of \(q\) | \(q = 0\) | |||
| effect of \(q\) | no vertical shift | |||
| value of \(a\) | \(a = 1\) | |||
| effect of \(a\) | increasing | |||
| asymptote |
\(x\)-axis, \(y = 0\) |
|||
| domain | \(\{x: x \in \mathbb{R} \}\) | |||
| range | \(\{y: y \in \mathbb{R}, y > 0 \}\) |
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | |
| value of \(q\) | \(q = 0\) | \(q = 0\) | \(q = 1\) | \(q = 2\) |
| effect of \(q\) | no vertical shift | no vertical shift | shift \(1\) unit up | shift \(2\) units down |
| value of \(a\) | \(a = 1\) | \(a = -2\) | \(a = 2\) | \(a = 1\) |
| effect of \(a\) | increasing | decreasing | increasing | increasing |
| asymptote |
\(x\)-axis, \(y = 0\) |
\(x\)-axis, \(y = 0\) |
\(y = 1\) |
\(y = -2\) |
| domain | \(\{x: x \in \mathbb{R} \}\) | \(\{x: x \in \mathbb{R} \}\) | \(\{x: x \in \mathbb{R} \}\) | \(\{x: x \in \mathbb{R} \}\) |
| range | \(\{y: y \in \mathbb{R}, y > 0 \}\) | \(\{y: y \in \mathbb{R}, y < 0 \}\) | \(\{y: y \in \mathbb{R}, y > 1 \}\) | \(\{y: y \in \mathbb{R}, y > -2 \}\) |
We now consider exponential functions of the form \(y=a{b}^{\left(x+p\right)}+q\) and the effects of parameter \(p\).
On the same system of axes, plot the following graphs:
Use your sketches of the functions above to complete the following table:
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | \(y_5\) | |
| intercept(s) | |||||
| asymptote | |||||
| domain | |||||
| range | |||||
| effect of \(p\) |
On the same system of axes, plot the following graphs:
Use your sketches of the functions above to complete the following table:
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | \(y_5\) | |
| intercept(s) | |||||
| asymptotes | |||||
| domain | |||||
| range | |||||
| effect of \(a\) |
The effect of the parameters on \(y = ab^{x + p} + q\)
The effect of \(p\) is a horizontal shift because all points are moved the same distance in the same direction (the entire graph slides to the left or to the right).
For \(p>0\), the graph is shifted to the left by \(p\) units.
For \(p<0\), the graph is shifted to the right by \(p\) units.
The effect of \(q\) is a vertical shift. The value of \(q\) also affects the horizontal asymptotes, the line \(y = q\).
The value of \(a\) affects the shape of the graph and its position relative to the horizontal asymptote.
For \(a>0\), the graph lies above the horizontal asymptote, \(y = q\).
For \(a<0\), the graph lies below the horizontal asymptote, \(y = q\).
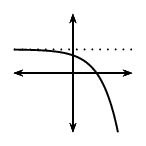
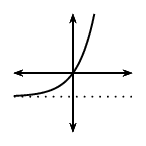
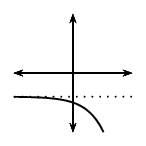
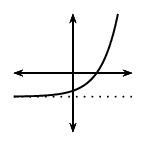
| \(p>0\) | \(p<0\) | |||
| \(a<0\) | \(a>0\) | \(a<0\) | \(a>0\) | |
| \(q>0\) |  |
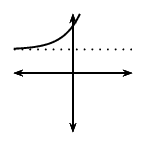 |
 |
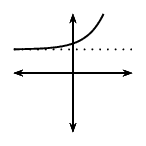 |
|
\(q<0\) |
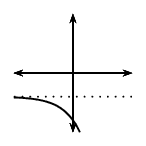 |
 |
 |
 |
For functions of the general form: \(f(x) = y = ab^{(x+p)} + q\):
Domain and range
The domain is \(\left\{x:x\in ℝ\right\}\) because there is no value of \(x\) for which \(f(x)\) is undefined.
The range of \(f(x)\) depends on whether the value for \(a\) is positive or negative.
If \(a>0\) we have: \begin{align*} {b}^{\left(x+p\right)} & > 0 \\ a {b}^{\left(x+p\right)} & > 0 \\ a {b}^{\left(x+p\right)} + q & > q \\ f(x) & > q \end{align*} The range is therefore \(\{ y: y > q, y \in \mathbb{R} \}\).
Similarly, if \(a < 0\), the range is \(\{ y: y < q, y \in \mathbb{R} \}\).
State the domain and range for \(g(x) = 5 \times 3^{(x+1)} - 1\).
The domain is \(\{x: x \in \mathbb{R} \}\) because there is no value of \(x\) for which \(g(x)\) is undefined.
The range of \(g(x)\) can be calculated from: \begin{align*} 3^{(x+1)} & > 0\\ 5 \times 3^{(x+1)} & > 0\\ 5 \times 3^{(x+1)} - 1 & > -1\\ \therefore g(x) & > -1 \end{align*} Therefore the range is \(\{g(x): g(x) > -1 \}\) or in interval notation \((-1; \infty)\).
Give the domain and range for each of the following functions:
\(y = \left( \frac{3}{2} \right)^{(x + 3)}\)
\(f(x) = -5^{(x - 2)} + 1\)
\(y + 3 = 2^{(x + 1)}\)
\(y = n + 3^{(x - m)}\)
\(\frac{y}{2} = 3^{(x - 1)} - 1\)
Intercepts
The \(y\)-intercept:
To calculate the \(y\)-intercept we let \(x=0\). For example, the \(y\)-intercept of \(g(x) = 3 \times 2^{(x + 1)} + 2\) is determined by setting \(x=0\): \begin{align*} g(0) &= 3 \times 2^{(0 + 1)} + 2 \\ &= 3 \times 2 + 2\\ &= 8 \end{align*} This gives the point \((0;8)\).
The \(x\)-intercept:
To calculate the \(x\)-intercept we let \(y=0\). For example, the \(x\)-intercept of \(g(x) = 3 \times 2^{(x + 1)} + 2\) is determined by setting \(y=0\): \begin{align*} 0 &= 3 \times 2^{(x + 1)} + 2 \\ -2 &= 3 \times 2^{(x + 1)} \\ -\frac{2}{3} &= 2^{(x + 1)} \end{align*} which has no real solutions. Therefore, the graph of \(g(x)\) lies above the \(x\)-axis and does not have any \(x\)-intercepts.
Determine the \(x\)- and \(y\)-intercepts for each of the following functions:
\(f(x) = 2^{(x + 1)} - 8\)
\(y = 2 \times 3^{(x - 1)} - \text{18}\)
\(y + 5^{(x + 2)} = 5\)
\(y = \frac{1}{2} \left( \frac{3}{2} \right)^{(x + 3)} - \text{0,75}\)
Asymptote
Exponential functions of the form \(y = ab^{(x+p)} + q\) have a horizontal asymptote, the line \(y = q\).
Determine the asymptote for \(y = 5 \times 3^{(x+1)} - 1\).
The asymptote of \(g(x)\) can be calculated as: \begin{align*} 3^{(x+1)} & \ne 0\\ 5 \times 3^{(x+1)} & \ne 0\\ 5 \times 3^{(x+1)} - 1 & \ne -1\\ \therefore y & \ne -1 \end{align*} Therefore the asymptote is the line \(y = -1\).
Give the asymptote for each of the following functions:
\(y = -5^{(x + 1)}\)
\(y = 3^{(x - 2)} + 1\)
\(\left( \frac{3y}{2} \right) = 5^{(x + 3)} - 1\)
\(y = 7^{(x + 1)} - 2\)
\(\frac{y}{2} + 1 = 3^{(x + 2)}\)
In order to sketch graphs of functions of the form, \(f(x)=a{b}^{\left(x+p\right)}+q\), we need to determine five characteristics:
shape
\(y\)-intercept
\(x\)-intercept
asymptote
domain and range
Sketch the graph of \(2y = \text{10} \times 2^{(x+1)} - 5\).
Mark the intercept(s) and asymptote. State the domain and range of the function.
We notice that \(a > 0\) and \(b > 1\), therefore the function is increasing.
The \(y\)-intercept is obtained by letting \(x = 0\): \begin{align*} 2y &= \text{10} \times 2^{(0+1)} - 5\\ &= \text{10} \times 2 - 5\\ &= \text{15}\\ \therefore y &= 7\frac{1}{2} \end{align*} This gives the point \((0;7\frac{1}{2})\).
The \(x\)-intercept is obtained by letting \(y = 0\): \begin{align*} 0 &= \text{10} \times 2^{(x+1)} - 5\\ 5 &= \text{10} \times 2^{(x+1)} \\ \frac{1}{2} &= 2^{(x+1)}\\ 2^{-1} &= 2^{(x+1)}\\ \therefore -1 &= x + 1 \quad \text{(same base)}\\ -2 &= x \end{align*} This gives the point \((-2;0)\).
The horizontal asymptote is the line \(y = -\frac{5}{2}\).
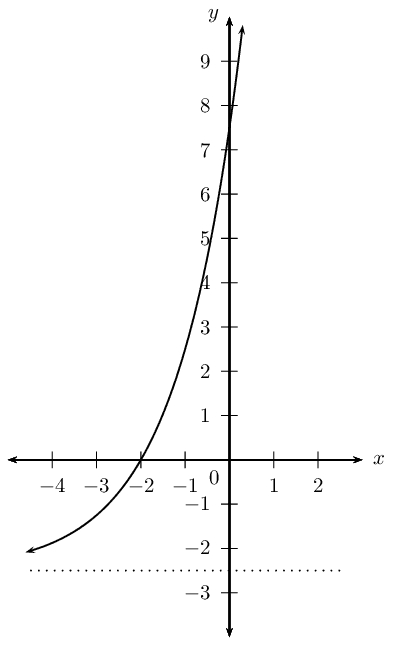
Domain: \(\{ x: x \in \mathbb{R} \}\)
Range: \(\{ y: y > -\frac{5}{2}, y \in \mathbb{R} \}\)
Finding the equation of an exponential function from the graph
Use the given graph of \(y = -2 \times 3^{(x + p)} + q\) to determine the values of \(p\) and \(q\).
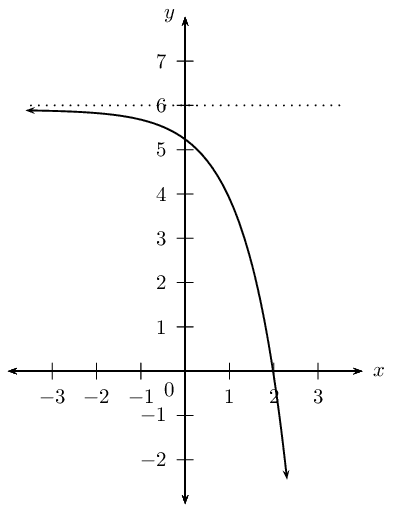
From the graph we see that the function is decreasing. We also note that \(a = -2\) and \(b = 3\).
We need to solve for \(p\) and \(q\).
The horizontal asymptote \(y = 6\) is given, therefore we know that \(q = 6\). \[y = -2 \times 3^{(x + p)} + 6\]
Substitute \((2;0)\) into the equation and solve for \(p\): \begin{align*} y &= -2 \times 3^{(x + p)} + 6 \\ 0 &= -2 \times 3^{(2 + p)} + 6 \\ -6 &= -2 \times 3^{(2 + p)} \\ 3 &= 3^{(2 + p)} \\ \therefore 1 &= 2 + p \quad \text{(same base)}\\ \therefore p &= -1 \end{align*}
\[y = -2 \times 3^{(x - 1)} + 6\]
Given the graph of the hyperbola of the form \(h(x) = \frac{k}{x}\), \(x < 0\), which passes though the point \(A(-\frac{1}{2}; -6)\).
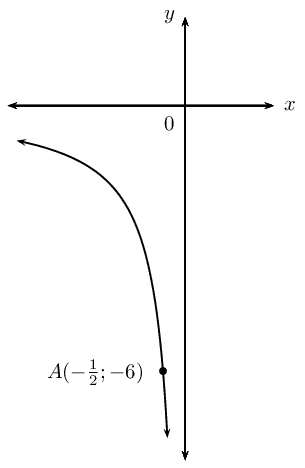
Show that \(k=3\).
Write down the equation for the new function formed if \(h(x)\):
is shifted \(\text{3}\) units vertically upwards
is shifted to the right by \(\text{3}\) units
is reflected about the \(y\)-axis
is shifted so that the asymptotes are \(x = 0\) and \(y = -\frac{1}{4}\)
is shifted upwards to pass through the point \((-1;1)\)
is shifted to the left by \(\text{2}\) units and \(\text{1}\) unit vertically downwards (for \(x < 0\))
Given the graphs of \(f(x) = a(x+p)^2\) and \(g(x) = \frac{a}{x}\).
The axis of symmetry for \(f(x)\) is \(x = -1\) and \(f(x)\) and \(g(x)\) intersect at point \(M\). The line \(y = 2\) also passes through \(M\).
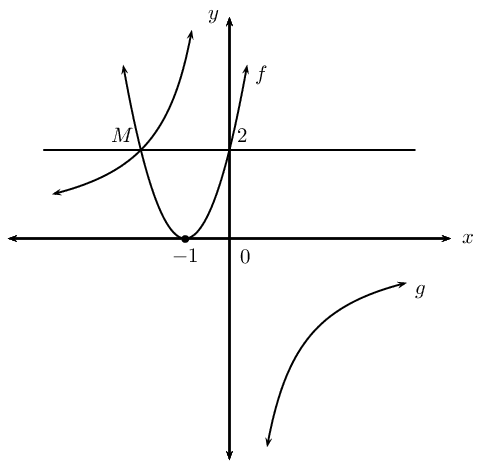
Determine:
the coordinates of \(M\)
\(f(x)\) is symmetrical about the line \(x = -1\), therefore \(M(-2;2)\).
the equation of \(g(x)\)
the equation of \(f(x)\)
the values for which \(f(x) < g(x)\)
the range of \(f(x)\)
On the same system of axes, sketch:
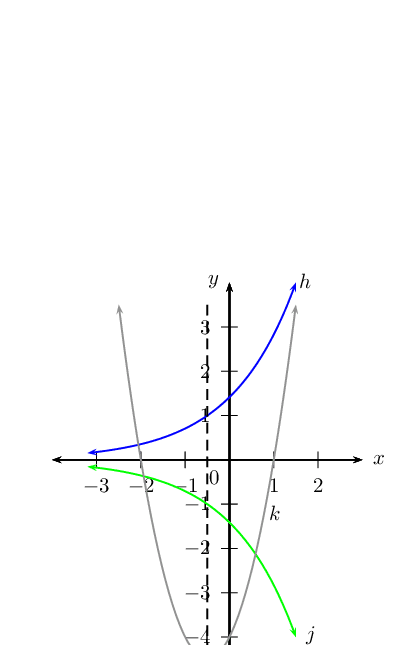
the graphs of \(k(x) = 2(x + \frac{1}{2})^2 - 4\frac{1}{2}\) and \(h(x) = 2^{(x + \frac{1}{2})}\). Determine all intercepts, turning point(s) and asymptotes.
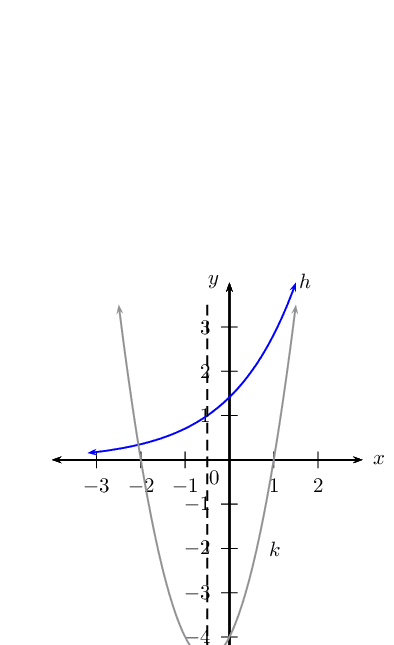
the reflection of \(h(x)\) about the \(x\)-axis. Label this function as \(j(x)\).
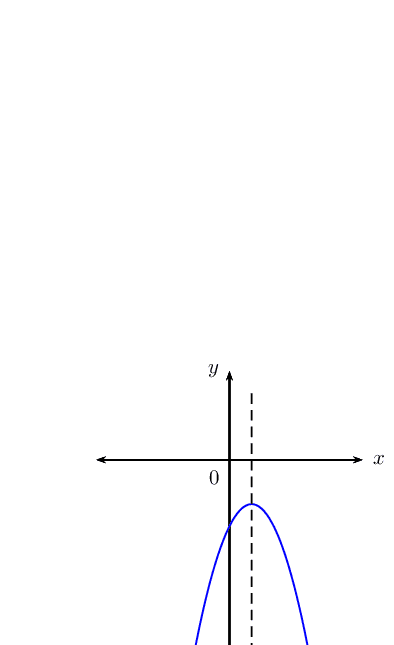
Sketch the graph of \(y = ax^2 + bx + c\) for:
\(a < 0\), \(b > 0\), \(b^2 < 4ac\)
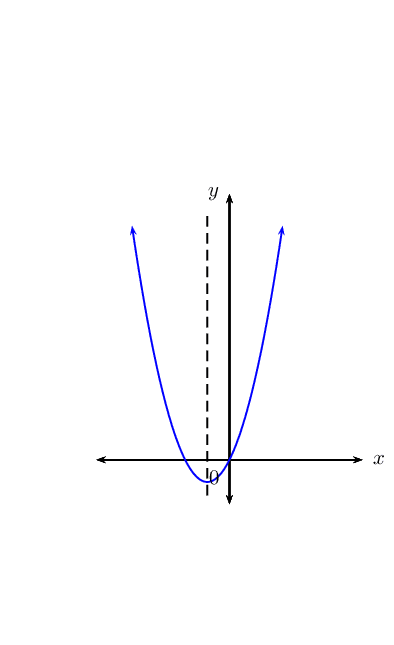
\(a > 0\), \(b > 0\), one root \(=0\)
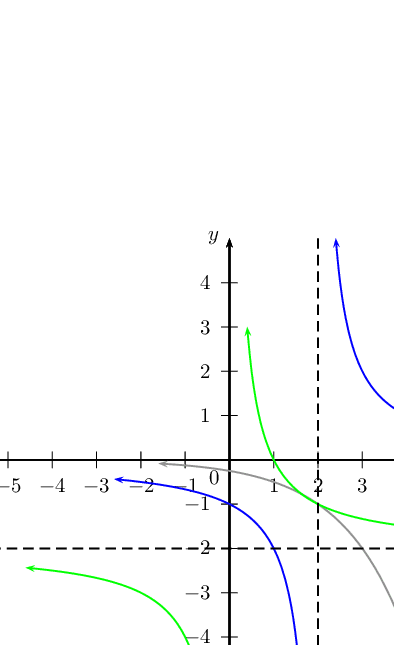
On separate systems of axes, sketch the graphs:
\(y = \frac{2}{x - 2}\)
\(y = \frac{2}{x} - 2\)
\(y = -2^{(x - 2)}\)
For the diagrams shown below, determine:
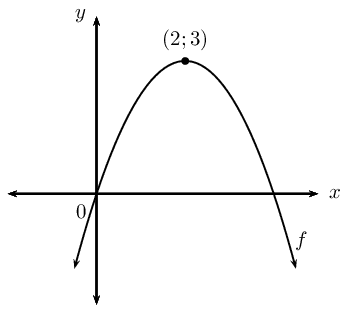
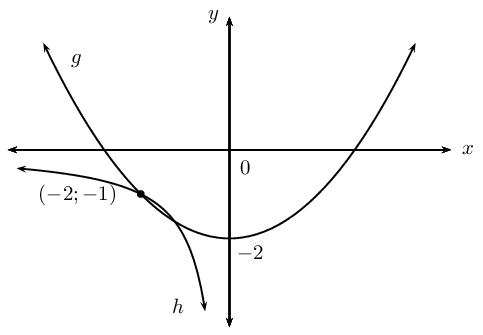
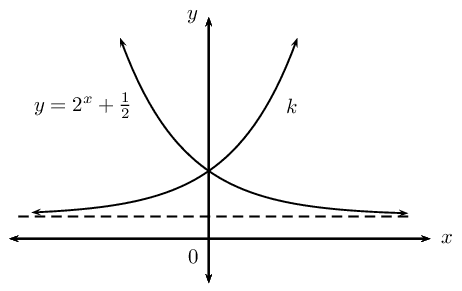
Given the graph of the function \(Q(x) = a^x\).
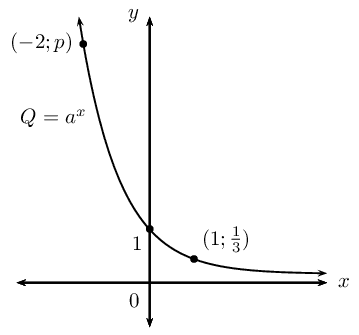
Show that \(a = \frac{1}{3}\).
Find the value of \(p\) if the point \((-2;p)\) is on \(Q\).
Calculate the average gradient of the curve between \(x = -2\) and \(x = 1\).
Determine the equation of the new function formed if \(Q\) is shifted \(\text{2}\) units vertically downwards and \(\text{2}\) units to the left.
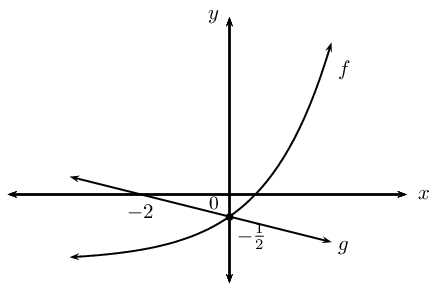
Find the equation for each of the functions shown below:
\(f(x) = 2^x + q\)
\(g(x) = mx + c\)
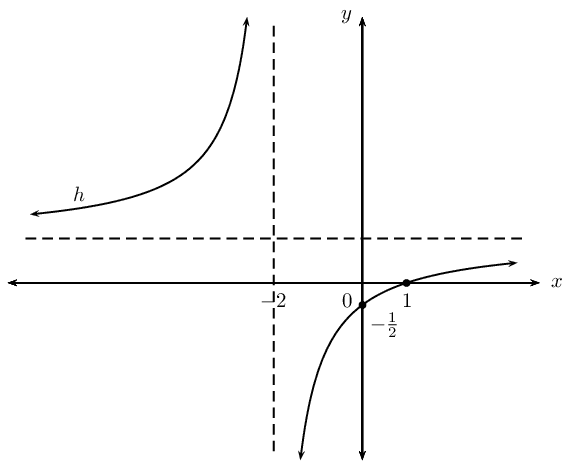
\(h(x) = \frac{k}{x + p} + q\)
Given: the graph of \(k(x) = -x^2 + 3x + \text{10}\) with turning point at \(D\). The graph of the straight line \(h(x) = mx + c\) passing through points \(B\) and \(C\) is also shown.
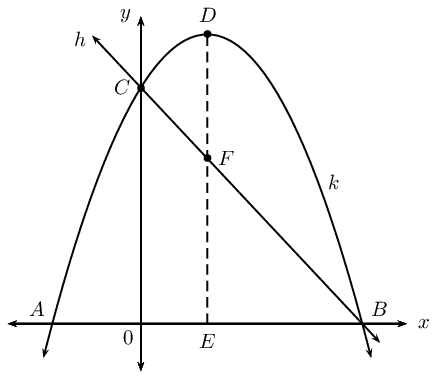
Determine:
the lengths \(AO\), \(OB\), \(OC\) and \(DE\)
the equation of \(DE\)
the equation of \(h(x)\)
the \(x\)-values for which \(k(x) < 0\)
the \(x\)-values for which \(k(x) \geq h(x)\)
the length of \(DF\)
Trigonometric functions are examined in PAPER 2.
|
Previous
5.3 Hyperbolic functions
|
Table of Contents |
Next
5.5 The sine function
|