End of chapter exercises
|
Previous
7.5 Summary
|
Next
8.1 Revision
|
End of chapter exercises
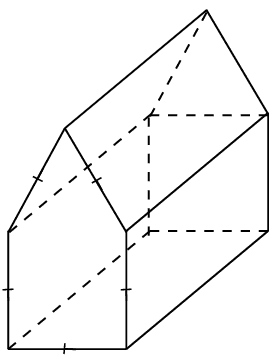
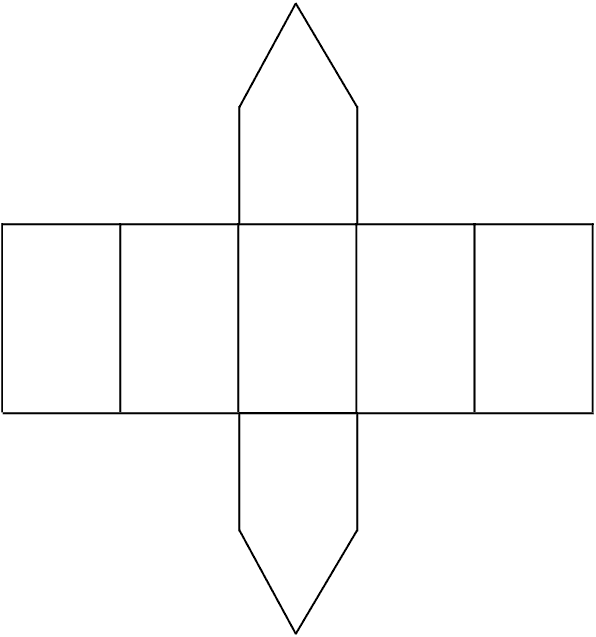
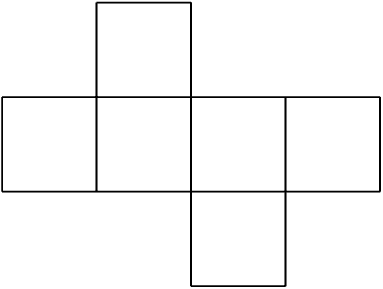
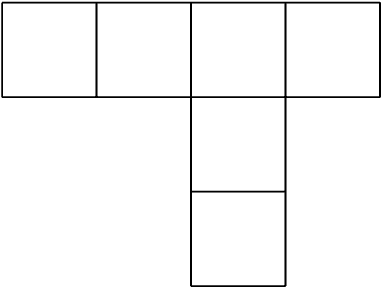
Which of the following is a net of a cube?
a and d
Name and draw the following figures:
Determine how much paper is needed to make a box of width \(\text{16}\) \(\text{cm}\), height \(\text{3}\) \(\text{cm}\) and length \(\text{20}\) \(\text{cm}\) (assume no overlapping at corners).
Determine how much paper is needed to make a cube with a capacity of \(\text{1}\) \(\text{L}\).
Compare the box and the cube. Which has the greater volume and which requires the most paper to make?
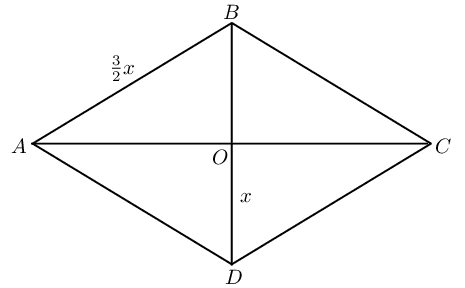
\(ABCD\) is a rhombus with sides of length \(\frac{3}{2}x\) millimetres. The diagonals intersect at \(O\) and length \(DO = x\) millimetres. Express the area of \(ABCD\) in terms of \(x\).
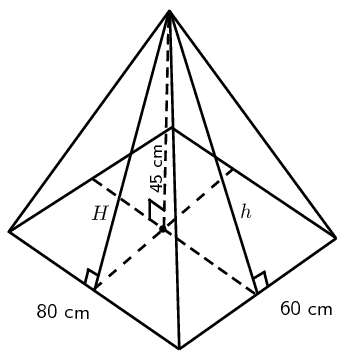
The diagram shows a rectangular pyramid with a base of length \(\text{80}\) \(\text{cm}\) and breadth \(\text{60}\) \(\text{cm}\). The vertical height of the pyramid is \(\text{45}\) \(\text{cm}\).
A group of children are playing soccer in a field. The soccer ball has a capacity of \(\text{5 000}\) \(\text{cc}\) (cubic centimetres). A drain pipe in the corner of the field has a diameter of \(\text{20}\) \(\text{cm}\). Is it possible for the children to lose their ball down the pipe? Show your calculations.
No, the ball is too big to go down the drain pipe.
A litre of washing powder goes into a standard cubic container at the factory.
A cube has sides of length \(k\) units.
|
Previous
7.5 Summary
|
Table of Contents |
Next
8.1 Revision
|