10.3 More Venn diagrams | Probability

10.3 More Venn diagrams (EMBJV)

In the rest of this chapter we will look at tools and techniques for working with probability problems.

When working with more complex problems, we can have three or more events that intersect in various ways. To solve these problems, we usually want to count the number (or percentage) of outcomes in an event, or a combination of events. Venn diagrams are a useful tool for recording and visualising the counts.

Venn diagram for $\text{3}$ events

The diagram below shows a general Venn diagram for $\text{3}$ events.

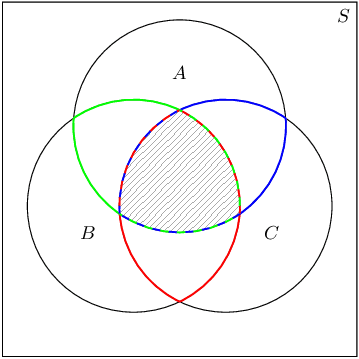
Write down the sets corresponding to each of the three coloured regions and also to the shaded region. Remember that the intersections between circles represent the intersections between the different events.

What is the event for

the red region;
the green region;
the blue region; and
the shaded region?

Worked example 8: Venn diagram for $\text{3}$ events

Draw a Venn diagram that shows the following sample space and events:

$S$ : all the integers from $\text{1}$ to $\text{30}$
$P$ : prime numbers
$M$ : multiples of $\text{3}$
$F$ : factors of $\text{30}$

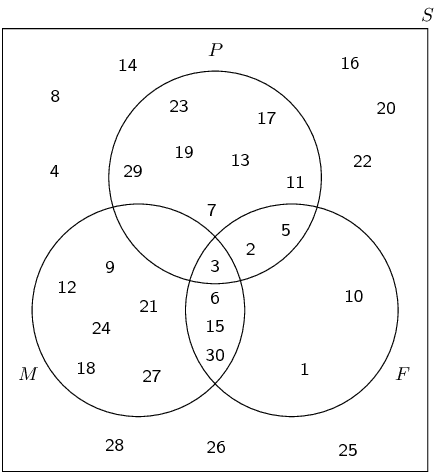
Write down the sample space and event sets

The sample space contains all the positive integers up to $\text{30}$ .

$S = \{1; 2; 3; \ldots; 30\}$

The prime numbers between $\text{1}$ and $\text{30}$ are

$P = \{2; 3; 5; 7; 11; 13; 17; 19; 23; 29\}$

The multiples of $\text{3}$ between $\text{1}$ and $\text{30}$ are

$M = \{3; 6; 9; 12; 15; 18; 21; 24; 27; 30\}$

The factors of $\text{30}$ are

$F = \{1; 2; 3; 5; 6; 10; 15; 30\}$

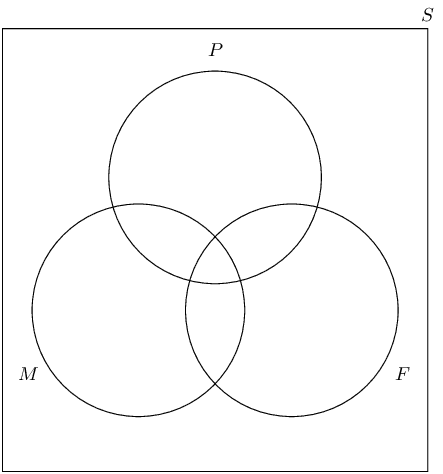
Draw the outline of the Venn diagram

There are $\text{3}$ events, namely $P$ , $M$ and $F$ , and the sample space, $S$ . Put this information on a Venn diagram:

Place the outcomes in the appropriate event sets

Worked example 9: Venn diagram for $\text{3}$ events

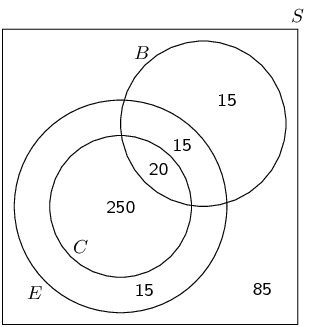
At Dawnview High there are $\text{400}$ Grade $\text{11}$ learners. $\text{270}$ do Computer Science, $\text{300}$ do English and $\text{50}$ do Business studies. All those doing Computer Science do English, $\text{20}$ take Computer Science and Business studies and $\text{35}$ take English and Business studies. Using a Venn diagram, calculate the probability that a pupil drawn at random will take:

English, but not Business studies or Computer Science
English but not Business studies
English or Business studies but not Computer Science
English or Business studies

Draw the outline of the Venn diagram

We need to be careful with this problem. In the question statement we are told that all the learners who do Computer Science also do English. This means that the circle for Computer Science on the Venn diagram needs to be inside the circle for English.

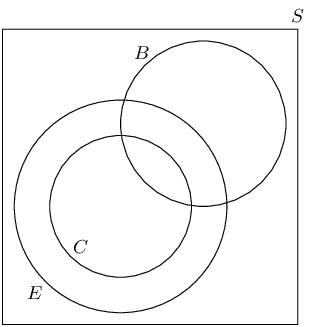
Fill in the counts on the Venn diagram

Compute probabilities

To find the number of learners taking English, but not Business studies or Computer Science, we need to look at this region of the Venn diagram:

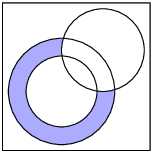
The count in this region is $\text{15}$ and there are a total of $\text{400}$ learners in the grade. Therefore the probability that a learner will take English but not Business studies or Computer Science is $\frac{15}{\text{400}} = \frac{3}{80}$ .

To find the number of learners taking English but not Business studies, we need to look at this region of the Venn diagram:

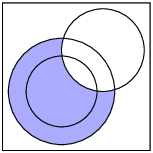
The count in this region is $\text{265}$ . Therefore the probability that a learner will take English but not Business studies is $\frac{\text{265}}{\text{400}} = \frac{53}{80}$ .

To find the number of learners taking English or Business studies but not Computer Science, we need to look at this region of the Venn diagram:

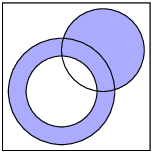
The count in this region is $\text{45}$ . Therefore the probability that a learner will take English or Business studies but not Computer Science is $\frac{45}{\text{400}} = \frac{9}{80}$ .

To find the number of learners taking English or Business studies, we need to look at this region of the Venn diagram:

The count in this region is $\text{315}$ . Therefore the probability that a learner will take English or Business studies is $\frac{\text{315}}{\text{400}} = \frac{63}{80}$ .

There are some words that tell you which part of the Venn diagram should be filled in. The following table summarises the most important ones:

Words	Symbols	Venn diagram
“all”	$A \text{ and } B \text{ and } C$ / $A \cap B \cap C$
“none”
“at least one”	$A \text{ or } B \text{ or } C$ / $A \cup B \cup C$
“both A and B”	$A \text{ and } B$ / $A \cap B$
“A or B”	$A \text{ or } B$ / $A \cup B$

Venn diagrams

Textbook Exercise 10.4

Compute $P(F)$.

$\frac{27}{120} = \frac{9}{40}$

Compute $P(G\text{ or }H)$.

$\frac{72}{120} = \frac{3}{5}$

Compute $P(F\text{ and }G)$.

$\frac{12}{120} = \frac{1}{10}$

Are $F$ and $G$ dependent or independent?

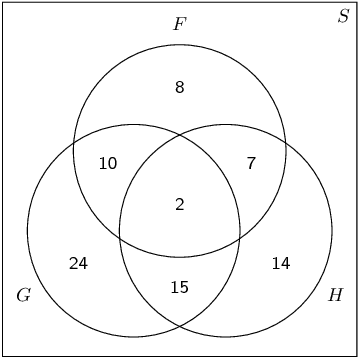
\begin{align*} P(F) \times P(G) &= \frac{9}{40} \times \frac{51}{120} \\ &= \frac{153}{1600} \end{align*} and \[P(F\text{ and }G) = \frac{1}{10}\] Therefore $P(F\text{ and }G) \ne P(F) \times P(G)$ and the events are dependent.

The Venn diagram below shows the probabilities of $\text{3}$ events. Complete the Venn diagram using the additional information provided.

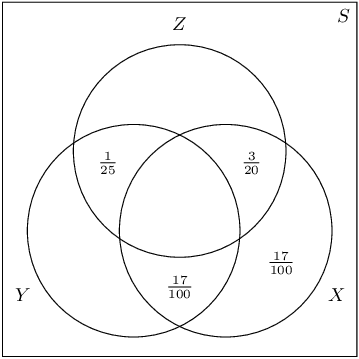
$P(Z\text{ and (not }Y)) = \frac{31}{\text{100}}$
$P(Y\text{ and }X) = \frac{23}{\text{100}}$
$P(Y) = \frac{39}{\text{100}}$

After completing the Venn diagram, compute the following: \[P\left(Z\text{ and not }(X\text{ or }Y)\right)\]

The completed Venn diagram is below.

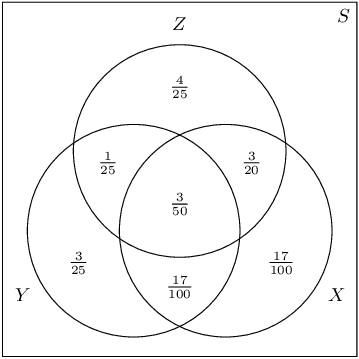
$\left(Z\text{ and not }(X\text{ or }Y)\right)$ is the top part of $Z$, which excludes all of $X$ and $Y$. Therefore $P\left(Z\text{ and not }(X\text{ or }Y)\right) = \frac{4}{25}$.

There are $\text{79}$ Grade $\text{10}$ learners at school. All of these take some combination of Maths, Geography and History. The number who take Geography is $\text{41}$; those who take History is $\text{36}$; and $\text{30}$ take Maths. The number who take Maths and History is $\text{16}$; the number who take Geography and History is $\text{6}$, and there are $\text{8}$ who take Maths only and $\text{16}$ who take History only.

Draw a Venn diagram to illustrate all this information.

How many learners take Maths and Geography but not History?

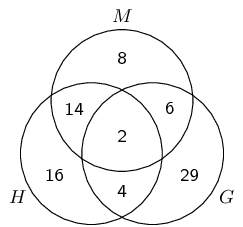
Each student must do exactly one of the following:

take only Geography;
only take Maths and/or History.

There are $30+36-16=50$ learners taking Maths and/or History, therefore there must be $79-50=29$ learners doing only Geography.

Each learner must do exactly one of the following:

take only Geography ($\text{29}$ learners);
take only Maths ($\text{8}$ learners);
take History ($\text{36}$ learners);
take Geography and Maths, but not History.

Given the number of learners list for each of the first three items above, the final answer is that $79-29-8-36 = \text{6}$ learners take Geography and Maths, but not History.

How many learners take Geography only?

Calculated already: $\text{29}$ learners.

How many learners take all three subjects?

Each learner must take exactly one of:

Geography;
only Maths;
only History;
Maths and History but not Geography.

Using the same method as before, the number of learners in the last group is $79-41-8-16 = 14$. But, $\text{16}$ learners do Maths and History, so there must be $16 - 14 = \text{2}$ learners who do all three.

Draw a Venn diagram with $\text{3}$ mutually exclusive events. Use the diagram to show that for $\text{3}$ mutually exclusive events, $A$, $B$ and $C$, the following is true: \[P(A\text{ or }B\text{ or }C) = P(A) + P(B) + P(C)\]

This is the addition rule for $\text{3}$ mutually exclusive events.

Recall for events to be mutually exclusive, they must have no elements in common. This mean that in the Venn diagram there must be no overlap between any of $A$, $B$ and $C$.

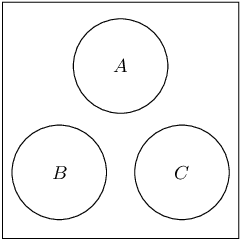
From the Venn diagram we can see that the probability of the three events together is simply the sum of their individual probabilities. So $P(A\text{ or }B\text{ or }C) = P(A) + P(B) + P(C)$. This will be true for any mutually exclusive events since they never overlap in the Venn diagram.

10.2 Dependent and independent events

Table of Contents

10.4 Tree diagrams

10.3 More Venn diagrams (EMBJV)

Venn diagram for 3\text{3} events

Worked example 8: Venn diagram for 3\text{3} events

Write down the sample space and event sets

Draw the outline of the Venn diagram

Place the outcomes in the appropriate event sets

Worked example 9: Venn diagram for 3\text{3} events

Draw the outline of the Venn diagram

Fill in the counts on the Venn diagram

Compute probabilities

Venn diagrams

Venn diagram for $\text{3}$ events

Worked example 8: Venn diagram for $\text{3}$ events

Worked example 9: Venn diagram for $\text{3}$ events