Write the following as a single trigonometric ratio: \(\dfrac{\cos (\text{90}\text{°} - A) \sin \text{20}\text{°}}{\sin (\text{180}\text{°} - A) \cos \text{70}\text{°}} + \cos (\text{180}\text{°} + A) \sin (\text{90}\text{°} + A)\)
End of chapter exercises
|
Previous
6.6 Summary
|
Next
7.1 Area of a polygon
|
End of chapter exercises
Determine the value of the following expression without using a calculator: \(\sin\text{240}\text{°} \cos\text{210}\text{°} - \tan^2 \text{225}\text{°} \cos\text{300}\text{°} \cos\text{180}\text{°}\)
Simplify: \(\dfrac{\sin (\text{180}\text{°} + \theta) \sin (\theta + \text{360}\text{°})}{\sin (-\theta) \tan (\theta - \text{360}\text{°})}\)
Without the use of a calculator, evaluate: \(\dfrac{3\sin \text{55}\text{°} \sin^2 \text{325}\text{°}}{\cos (-\text{145}\text{°})} - 3\cos \text{395}\text{°} \sin \text{125}\text{°}\)
Prove the following identities:
Prove: \(\tan y + \dfrac{1}{\tan y} = \dfrac{1}{\cos^2y \tan y}\)
For which values of \(y \in [\text{0}\text{°};\text{360}\text{°}]\) is the identity above undefined?
Simplify: \(\dfrac{\sin(\text{180}\text{°} + \theta) \tan(\text{360}\text{°} - \theta)}{\sin(-\theta) \tan(\text{180}\text{°} + \theta)}\)
Hence, solve the equation \(\dfrac{\sin(\text{180}\text{°} + \theta) \tan(\text{360}\text{°} - \theta)}{\sin(-\theta) \tan(\text{180}\text{°} + \theta)} = \tan \theta\) for \(\theta \in [\text{0}\text{°};\text{360}\text{°}]\).
Given \(12 \tan \theta = 5\) and \(\theta > \text{90}\text{°}\).
Draw a sketch.
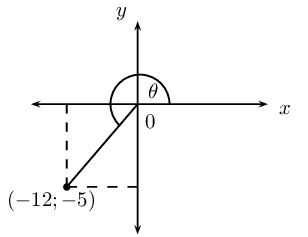
Determine without using a calculator \(\sin \theta\) and \(\cos (\text{180}\text{°} + \theta)\).
Use a calculator to find \(\theta\) (correct to two decimal places).
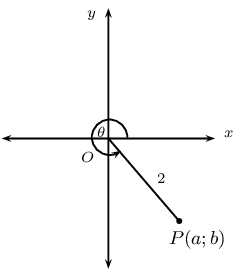
In the figure, \(P\) is a point on the Cartesian plane such that \(OP = 2\) units and \(\theta = \text{300}\text{°}\). Without the use of a calculator, determine:
the values of \(a\) and \(b\)
the value of \(\sin (\text{180}\text{°} - \theta)\)
Solve for \(x\) with \(x \in [-\text{180}\text{°};\text{180}\text{°}]\) (correct to one decimal place):
Find the general solution for the following equations:
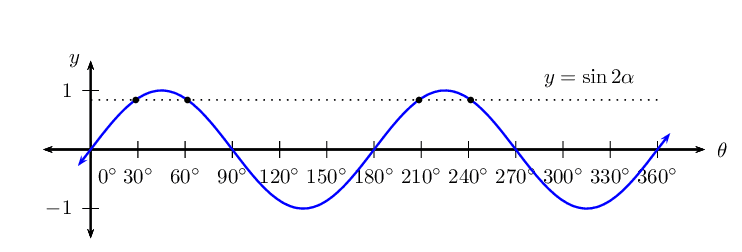
Given the equation: \(\sin 2 \alpha = \text{0,84}\)
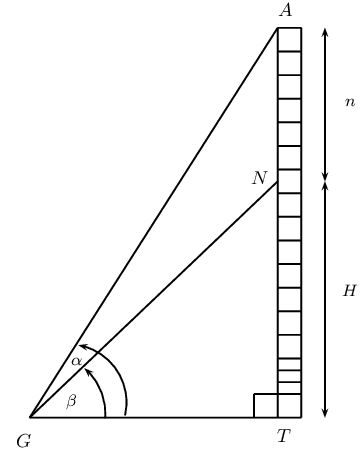
\(A\) is the highest point of a vertical tower \(AT\). At point \(N\) on the tower, \(n\) metres from the top of the tower, a bird has made its nest. The angle of inclination from \(G\) to point \(A\) is \(\alpha\) and the angle of inclination from \(G\) to point \(N\) is \(\beta\).
Express \(A\hat{G}N\) in terms of \(\alpha\) and \(\beta\).
Express \(\hat{A}\) in terms of \(\alpha\) and/or \(\beta\).
Show that the height of the nest from the ground (\(H\)) can be determined by the formula \[H = \frac{n \cos \alpha \sin \beta}{\sin(\alpha - \beta)}\]
Calculate the height of the nest \(H\) if \(n = \text{10}\text{ m}\), \(\alpha = \text{68}\text{°}\) and \(\beta = \text{40}\text{°}\) (give your answer correct to the nearest metre).
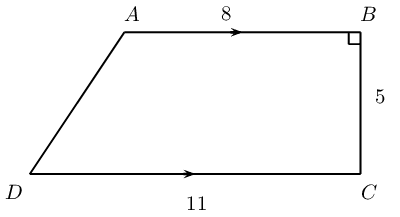
Mr. Collins wants to pave his trapezium-shaped backyard, \(ABCD\). \(AB \parallel DC\) and \(\hat{B} = \text{90}\text{°}\). \(DC = \text{11}\text{ m}\), \(AB = \text{8}\text{ m}\) and \(BC = \text{5}\text{ m}\).
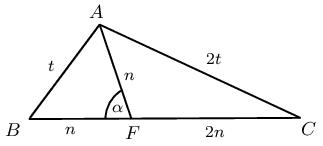
In \(\triangle ABC\), \(AC = 2A\), \(AF = BF\), \(A\hat{F}B = \alpha\) and \(FC = 2AF\). Prove that \(\cos \alpha = \frac{1}{4}\).
|
Previous
6.6 Summary
|
Table of Contents |
Next
7.1 Area of a polygon
|
