7.4 Summary
|
Previous
7.3 Equation of a tangent to a circle
|
Next
End of chapter exercises
|
7.4 Summary (EMCHX)
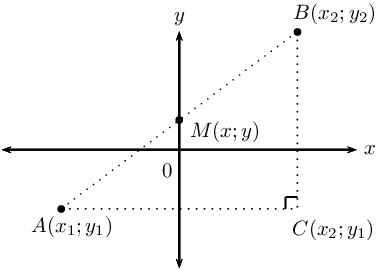
| Theorem of Pythagoras: | \(AB^2 = AC^2 + BC^2\) |
| Distance formula: | \(AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\) |
| Gradient: | \(m_{AB} = \frac{y_2 - y_1}{x_2 - x_1} \quad \text{ or } \quad m_{AB} = \frac{y_1 - y_2}{x_1 - x_2}\) |
| Mid-point of a line segment: | \(M(x;y) = \left( \frac{x_1 + x_2}{2}; \frac{y_1 + y_2}{2} \right)\) |
| Points on a straight line: | \(m_{AB} = m_{AM} = m_{MB}\) |
| Straight line equations | Formulae |
| Two-point form: | \(\dfrac{y - y_1}{x - x_1} = \dfrac{y_2 - y_1}{x_2 - x_1}\) |
| Gradient-point form: | \(y - y_1 = m (x - x_{1})\) |
| Gradient-intercept form: | \(y = mx + c\) |
| Horizontal lines: | \(y = k\) |
| Vertical lines | \(x = k\) |
| Parallel lines | 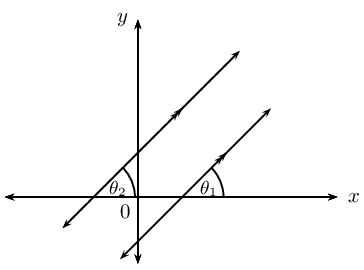 |
\(m_1 = m_2\) | \(\theta_1 = \theta_2\) |
| Perpendicular lines | 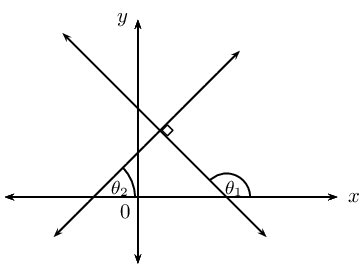 |
\(m_1 \times m_2 = -1\) | \(\theta_{1} = \text{90} ° + \theta_{2}\) |
-
Inclination of a straight line: the gradient of a straight line is equal to the tangent of the angle formed between the line and the positive direction of the \(x\)-axis.
\[m = \tan \theta \qquad \text{ for } \text{0}° \leq \theta < \text{180}°\]
-
Equation of a circle with centre at the origin:
If \(P(x;y)\) is a point on a circle with centre \(O(0;0)\) and radius \(r\), then the equation of the circle is:
\[x^{2} + y^{2} = r^{2}\] -
General equation of a circle with centre at \((a;b)\):
If \(P(x;y)\) is a point on a circle with centre \(C(a;b)\) and radius \(r\), then the equation of the circle is:
\[(x - a)^{2} + (y - b)^{2} = r^{2}\] -
A tangent is a straight line that touches the circumference of a circle at only one point.
-
The radius of a circle is perpendicular to the tangent at the point of contact.
|
Previous
7.3 Equation of a tangent to a circle
|
Table of Contents |
Next
End of chapter exercises
|
