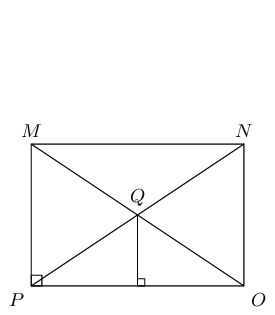
Calculate \(MN\) (correct to \(\text{2}\) decimal places).
8.3 Polygons
|
Previous
8.2 Ratio and proportion
|
Next
8.4 Triangles
|
8.3 Polygons (EMCJ9)
- Proportionality in polygons
-
A plane, closed shape consisting of three or more line segments.
In previous grades we studied the properties of the following polygons:
| Triangle | 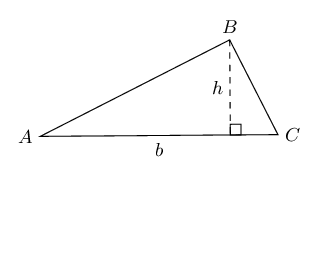 |
Area \(= \frac{1}{2}b \times h\) |
| Parallelogram | 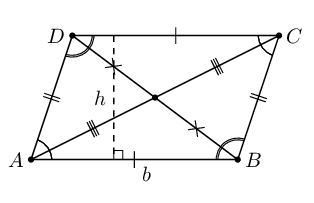 |
Area \(= b \times h\) |
| Rectangle | 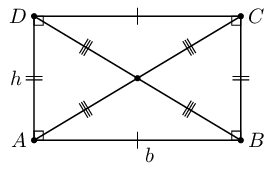 |
Area \(= b \times h\) |
| Rhombus | 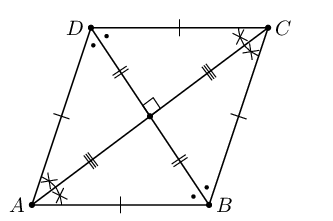 |
Area \(= \frac{1}{2} AC \times BD\) |
| Square | 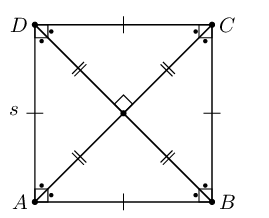 |
Area \(= s^{2}\) |
| Trapezium | 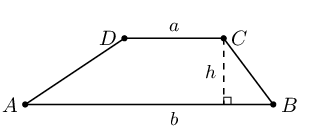 |
Area \(= \frac{1}{2}(a + b) \times h\) |
| Kite | 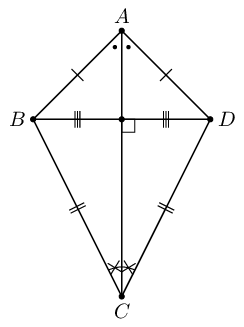 |
Area \(= \frac{1}{2}(AC \times DB)\) |
Worked example 1: Properties of polygons
\(ABCD\) is a rhombus with \(BD = \text{12}\text{ cm}\) and \(AB:BD = 3:4\).
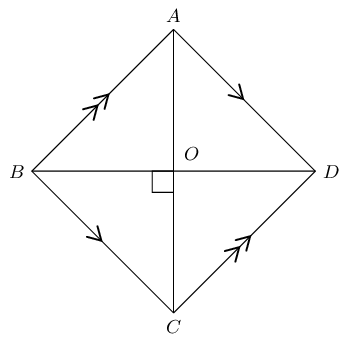
Calculate the following (correct to two decimal places) and provide reasons:
- Length of \(AB\).
- Length of \(AO\).
- Area of \(ABCD\).
Use the ratio to determine the length of \(AB\)
\begin{align*} AB:BD &= 3:4 \\ \therefore \frac{AB}{BD} &= \frac{3}{4} \\ \frac{AB}{12} &= \frac{3}{4} \\ AB &= 12 \times \frac{3}{4} \\ &= \text{9}\text{ cm} \end{align*}Calculate the length of \(AO\)
We use the properties of a rhombus and the theorem of Pythagoras to find \(AO\).
\[\begin{array}{rll} BD &= \text{12}\text{ cm} & \\ BO &= \text{6}\text{ cm} & \text{(diagonals bisect each other)} \\ \text{In } \triangle ABO, \quad A\hat{O}B &= \text{90}° & (\text{diagonals intersect at } \perp )\\ AO^{2} &= AB^{2} - BO^{2} & (\text{Pythagoras}) \\ &= 9^{2} - 6^{2} & \\ \therefore AO &= \sqrt{ 45} & \\ &= \text{6,71}\text{ cm} \end{array}\]Determine the area of rhombus \(ABCD\)
\begin{align*} \text{Area } ABCD &= \frac{1}{2} AC \times BD \\ &= \frac{1}{2} (2 \times \sqrt{45})(12) \\ &= \text{80,50}\text{ cm$^{2}$} \end{align*}Proportionality of polygons
\(MNOP\) is a rectangle with \(MN : NO = 5:3\) and \(QN = \text{10}\text{ cm}\).
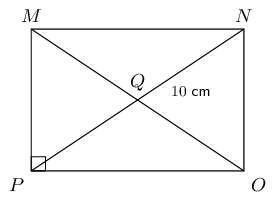
Calculate the area of \(\triangle OPQ\) (correct to \(\text{2}\) decimal places).
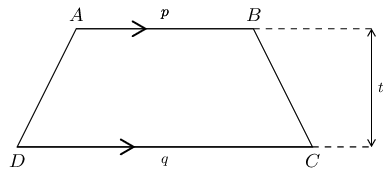
Consider the trapezium \(ABCD\) shown below. If \(t:p:q = 2:3:5\) and area \(ABCD = \text{288}\text{ cm$^{2}$}\), calculate \(t, p \text{ and } q\).
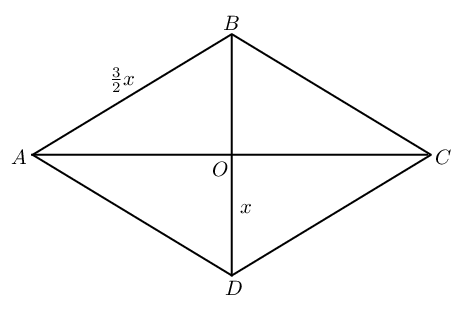
\(ABCD\) is a rhombus with sides of length \(\frac{3}{2}x\) millimetres. The diagonals intersect at \(O\) and length \(DO = x\) millimetres. Express the area of \(ABCD\) in terms of \(x\).
In the diagram below, \(FGHI\) is a kite with \(FG = \text{6}\text{ mm}\), \(GK = \text{4}\text{ mm}\) and \(\frac{GH}{FI} = \frac{5}{2}\).
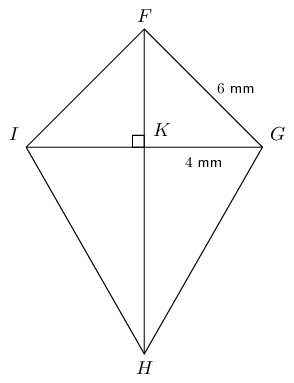
Determine \(FH\) (correct to the nearest integer).
Calculate area \(FGHI\).
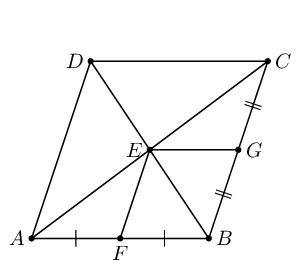
\(ABCD\) is a rhombus. \(F\) is the mid-point of \(AB\) and \(G\) is the mid-point of \(CB\). Prove that \(EFBG\) is also a rhombus.
|
Previous
8.2 Ratio and proportion
|
Table of Contents |
Next
8.4 Triangles
|
