Given \(f\left(x\right)=5x + 4\), find \({f}^{-1}\left(x\right)\).
2.4 Linear functions
|
Previous
2.3 Inverse functions
|
Next
2.5 Quadratic functions
|
2.4 Linear functions (EMCF9)
Inverse of the function \(y=ax+q\) (EMCFB)
Worked example 4: Inverse of the function \(y=ax+q\)
Determine the inverse function of \(p(x) = -3x + 1\) and sketch the graphs of \(p(x)\) and \(p^{-1}(x)\) on the same system of axes.
Determine the inverse of the given function
- Interchange \(x\) and \(y\) in the equation.
- Make \(y\) the subject of the new equation.
- Express the new equation in function notation.
Therefore, \(p^{-1}(x) = -\frac{x}{3} + \frac{1}{3}\).
Sketch the graphs of the same system of axes
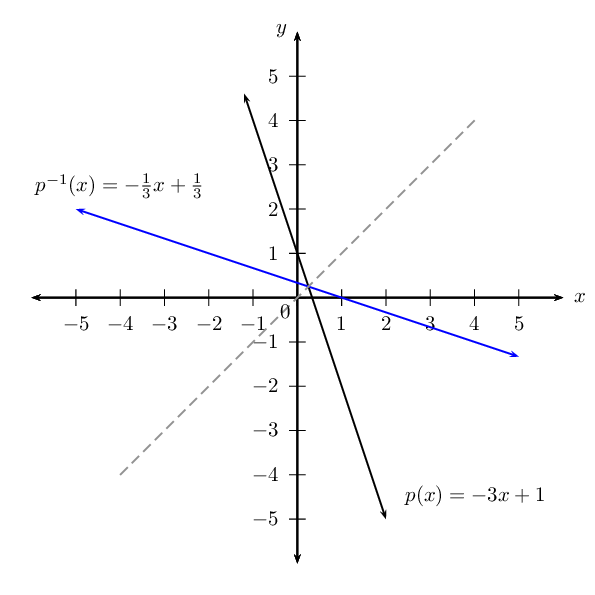
The graph of \(p^{-1}(x)\) is the reflection of \(p(x)\) about the line \(y = x\). This means that every point on the graph of \(p(x)\) has a mirror image on the graph of \(p^{-1}(x)\).
To determine the inverse function of \(y=ax+q\):
\[\begin{array}{rll} &(1) \quad \text{Interchange } x \text{ and } y: & x = ay+q \\ &(2) \quad \text{Make } y \text{ the subject of the equation}: & x - q = ay \\ && \frac{x}{a} - \frac{q}{a} = \frac{ay}{a} \\ &&\therefore y = \frac{1}{a}x-\frac{q}{a} \end{array}\]Therefore the inverse of \(y=ax+q\) is \(y=\frac{1}{a}x-\frac{q}{a}\). If a linear function is invertible, then its inverse will also be linear.
Worked example 5: Inverses - domain, range and intercepts
Determine and sketch the inverse of the function \(f(x) = 2x - 3\). State the domain, range and intercepts.
Determine the inverse of the given function
- Interchange \(x\) and \(y\) in the equation.
- Make \(y\) the subject of the new equation.
- Express the new equation in function notation.
Therefore, \(f^{-1}(x) = \frac{x}{2} + \frac{3}{2}\).
Sketch the graphs on the same system of axes
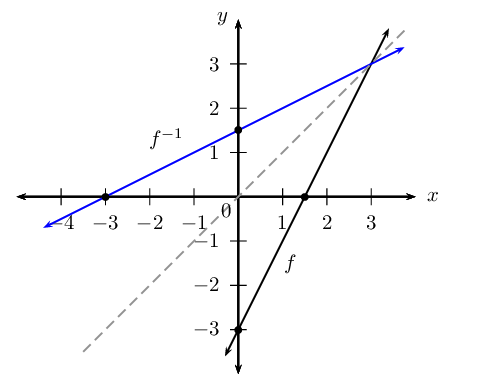
The graph of \(f^{-1}(x)\) is the reflection of \(f(x)\) about the line \(y = x\).
Determine domain, range and intercepts
\begin{align*} \text{Domain of } f &: \{ x: x \in \mathbb{R} \} \\ \text{Range of } f &: \{ y: y \in \mathbb{R} \} \\ \text{Intercepts of } f &: (0;-3) \text{ and } \left(\frac{3}{2}; 0 \right) \\ & \\ \text{Domain of } f^{-1} &: \{ x: x \in \mathbb{R} \} \\ \text{Range of } f^{-1} &: \{ y: y \in \mathbb{R} \} \\ \text{Intercepts of } f^{-1} &: \left(0;\frac{3}{2}\right) \text{ and } (-3;0) \end{align*}Notice that the intercepts of \(f\) and \(f^{-1}\) are mirror images of each other. In other words, the \(x\)- and \(y\)-values have “swapped” positions. This is true of every point on the two graphs.
Domain and range
For a function of the form \(y=ax+q\), the domain is \(\left\{x:x\in ℝ\right\}\) and the range is \(\left\{y:y\in ℝ\right\}\). When a function is inverted the domain and range are interchanged. Therefore, the domain and range of the inverse of an invertible, linear function will be \(\left\{x:x\in ℝ\right\}\) and \(\left\{y:y\in ℝ\right\}\) respectively.
Intercepts
The general form of an invertible, linear function is \(y=ax+q \enspace (a \ne 0)\) and its inverse is \(y=\frac{1}{a}x-\frac{q}{a}\).
The \(y\)-intercept is obtained by letting \(x=0\):
\begin{align*} y &= \frac{1}{a}(0)-\frac{q}{a} \\ y &= -\frac{q}{a} \end{align*}This gives the point \(\left(0; -\frac{q}{a}\right)\).
The \(x\)-intercept is obtained by letting \(y=0\):
\begin{align*} 0 &= \frac{1}{a}x -\frac{q}{a} \\ \frac{q}{a} &= \frac{1}{a}x \\ q &= x \end{align*}This gives the point \((q; 0)\).
It is interesting to note that if \(f\left(x\right)=ax+q \enspace (a \ne 0)\), then \({f}^{-1}\left(x\right)=\frac{1}{a}x-\frac{q}{a}\) and the \(y\)-intercept of \(f\left(x\right)\) is the \(x\)-intercept of \({f}^{-1}\left(x\right)\) and the \(x\)-intercept of \(f\left(x\right)\) is the \(y\)-intercept of \({f}^{-1}\left(x\right)\).
Inverse of the function \(y = ax + q\)
Consider the relation \(f\left(x\right)=-3x-7\).
Is the relation a function? Explain your answer.
It is a function. Every \(x\)-value relates to only one \(y\)-value, it is a one-to-one relation.
Identify the domain and range.
Determine \(f^{-1}(x)\).
Sketch the graph of the function \(f\left(x\right)=3x-1\) and its inverse on the same system of axes. Indicate the intercepts and the axis of symmetry of the two graphs.
The intercepts are:
\begin{align*} f(x): x = 0, y = -\text{1}\\ y=0, x = \frac{1}{3}\\ f^{-1}(x): x = 0, y = \frac{1}{3}\\ y = 0, x = -\text{1} \end{align*}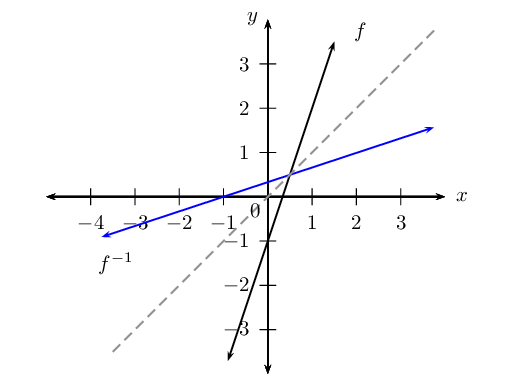
\(T\left( \frac{4}{3}; 3 \right)\) is a point on \(f\) and \(R\) is a point on \(f^{-1}\). Determine the coordinates of \(R\) if \(R\) and \(T\) are symmetrical.
Explain why the line \(y = x\) is an axis of symmetry for a function and its inverse.
To reflect a function about the \(y\)-axis, we replace every \(x\) with \(-x\). Similarly, to reflect a function about the \(x\)-axis, we replace every \(y\) with \(-y\). To reflect a function about the line \(y=x\), we replace \(x\) with \(y\) and \(y\) with \(x\), which is how we determine the inverse.
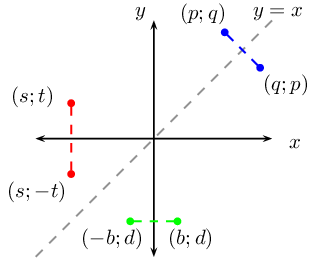
Will the line \(y = -x\) be an axis of symmetry for a function and its inverse?
Given \({f}^{-1}\left(x\right)=-2x+4\), determine \(f\left(x\right)\).
Calculate the intercepts of \(f(x)\) and \(f^{-1}(x)\).
Consider \(f(x)\):
\begin{align*} \text{Let } y & = -\frac{1}{2}x + 2 \\ \text{Let } x=0: \quad y & = -\frac{1}{2}(0) + 2 \\ y & = 2 \\ \therefore y &-\text{intercept is } (0;2) \\ & \\ \text{Let } y=0: \quad 0 & = -\frac{1}{2}x + 2 \\ -2 & = -\frac{1}{2}x \\ x & = 4 \\ \therefore x &-\text{intercept is } (4;0) \end{align*}Consider \(f^{-1}(x)\):
\begin{align*} \text{Let } y & = - 2x+4 \\ \text{Let } x=0: \quad y & = - 2(0) + 4\\ y & = 4 \\ \therefore y &-\text{intercept is } (0;4) \\ & \\ \text{Let } y=0: \quad 0 & = - 2x+4\\ 2x & = 4 \\ x & = 2 \\ \therefore x &-\text{intercept is } (2;0) \end{align*}Therefore the intercepts for \(f(x)\) are \((4;0)\) and \((0;2)\) and the intercepts for \(f^{-1}(x)\) are \((2;0)\) and \((0;4)\).
Determine the coordinates of \(T\), the point of intersection of \(f(x)\) and \(f^{-1}(x)\).
To find the point on intersection, we let \(f(x) = f^{-1}(x)\):
\begin{align*} -\frac{1}{2}x + 2 & = -2x + 4 \\ -\frac{1}{2}x + 2x & = 4 - 2 \\ \frac{3}{2}x & = 2 \\ \therefore x & = \frac{4}{3} \\ \text{And } y & = -2 \left( \frac{4}{3} \right) + 4 \\ & = - \frac{8}{3} + 4 \\ & = \frac{4}{3} \end{align*}This gives the point \(T \left( \frac{4}{3};\frac{4}{3} \right)\).
Sketch the graphs of \(f\) and \(f^{-1}\) on the same system of axes. Indicate the intercepts and point \(T\) on the graph.
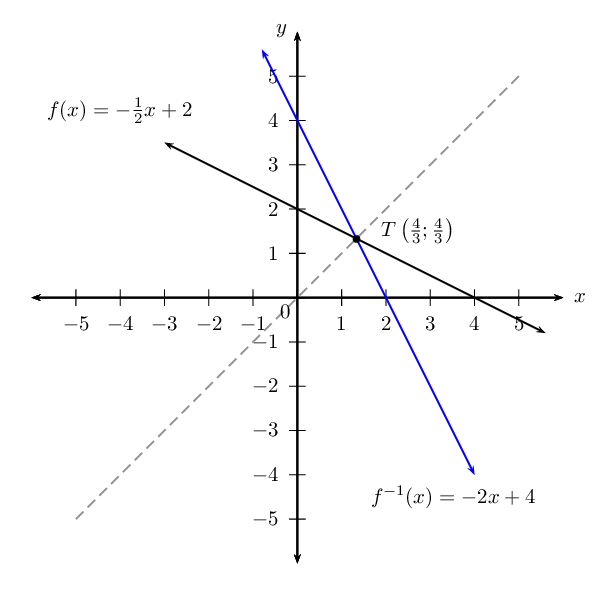
Is \(f^{-1}\) an increasing or decreasing function?
Decreasing function. The function values decrease as \(x\) increases.
|
Previous
2.3 Inverse functions
|
Table of Contents |
Next
2.5 Quadratic functions
|
