|
Previous
4.1 Revision
|
Next
4.3 Double angle identities
|
Danny is studying for a trigonometry test and completes the following question:
Question:
Evaluate the following:
\(\cos \left( \text{180} ° - \text{120} ° \right)\)
Danny's solution:
\[\begin{array}{rll} \cos \left( \text{180} ° - \text{120} ° \right) &= \cos \text{180} ° - \cos \text{120} ° & (\text{line } 1 )\\ &= -1 - \cos \left( \text{90} ° + \text{30} ° \right) & (\text{line } 2 ) \\ &= - 1 + \sin \text{30} ° & (\text{line } 3 ) \\ &= -1 + \frac{1}{2} & (\text{line } 4 ) \\ &= -\frac{1}{2} & (\text{line } 5 ) \end{array}\]Is the following statement true or false?
"A trigonometric ratio can be distributed to the angles that lie within the brackets."
From the investigation above, we know that \(\cos (\alpha - \beta) \ne \cos \alpha - \cos \beta\). It is wrong to apply the distributive law to the trigonometric ratios of compound angles.
\begin{align*} \text{Distance formula: } \quad d_{AB} &= \sqrt{ {\left({x}_{A}-{x}_{B}\right)}^{2}+{\left({y}_{A}-{y}_{B}\right)}^{2} } \\ \text{Cosine rule: } \quad a^{2} &= b^{2} + c^{2} - 2bc \cdot \cos \hat{A} \end{align*}Using the distance formula and the cosine rule, we can derive the following identity for compound angles:
\[\cos\left(\alpha -\beta \right) = \cos \alpha \cos\beta +\sin\alpha \sin\beta\]
Consider the unit circle \((r = 1)\) below. The two points \(L\left(a;b\right)\) and \(K\left(x;y\right)\) are shown on the circle.
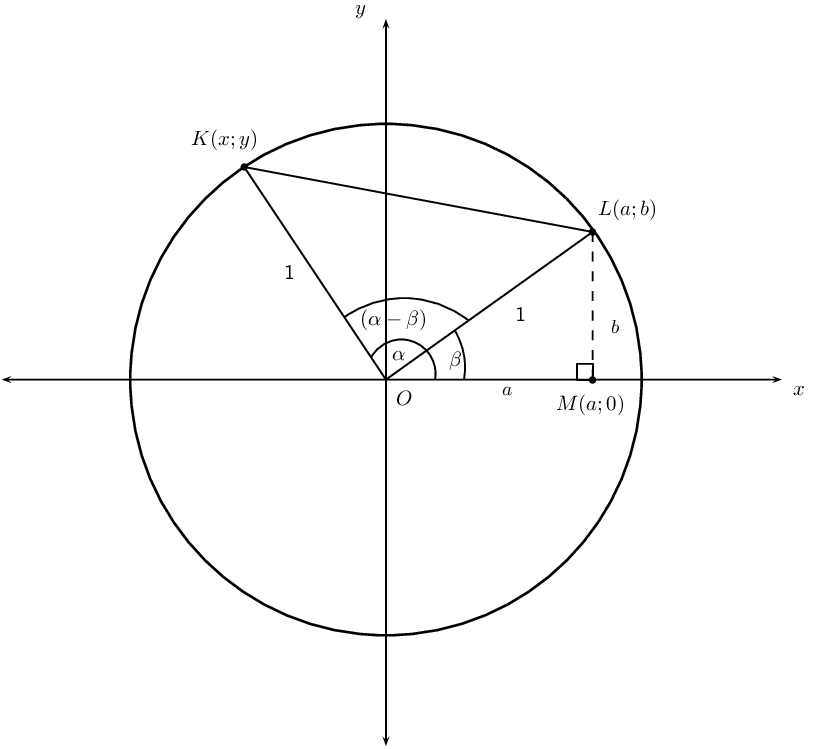
We can express the coordinates of \(L\) and \(K\) in terms of the angles \(\alpha\) and \(\beta\):
\begin{align*} \text{In } \triangle LOM, \quad \sin \beta &= \frac{b}{1} \\ \therefore b &=\sin\beta \\ \cos \beta &=\frac{a}{1} \\ \therefore a &=\cos\beta \\ & \\ L &= \left(\cos\beta ;\sin\beta \right) \\ & \\ \text{Similarly, } K &=\left(\cos\alpha ;\sin\alpha \right) \end{align*}We use the distance formula to determine \(K{L}^{2}\):
\begin{align*} {d}^{2} &= {\left({x}_{K}-{x}_{L}\right)}^{2}+{\left({y}_{K}-{y}_{L}\right)}^{2} \\ K{L}^{2}& = {\left(\cos\alpha -\cos\beta \right)}^{2}+{\left(\sin\alpha -\sin\beta \right)}^{2} \\ & = {\cos}^{2}\alpha -2\cos\alpha\cos \beta +{\cos}^{2}\beta +{\sin}^{2}\alpha -2\sin\alpha\sin \beta +{\sin}^{2}\beta \\ & = \left({\cos}^{2}\alpha +{\sin}^{2}\alpha \right)+\left({\cos}^{2}\beta +{\sin}^{2}\beta \right)-2\cos\alpha\cos \beta -2\sin\alpha\sin \beta \\ & = 1+1-2\left(\cos\alpha\cos \beta +\sin\alpha\sin \beta \right) \\ & = 2-2\left(\cos\alpha\cos \beta +\sin\alpha\sin \beta \right) \end{align*}Now we determine \(K{L}^{2}\) using the cosine rule for \(\triangle KOL\):
\begin{align*} K{L}^{2}& = K{O}^{2}+L{O}^{2}-2 \cdot KO \cdot LO \cdot \cos\left(\alpha -\beta \right) \\ & = {1}^{2}+{1}^{2}-2\left(1\right)\left(1\right)\cos\left(\alpha -\beta \right) \\ & = 2-2 \cdot \cos\left(\alpha -\beta \right) \end{align*}Equating the two expressions for \(K{L}^{2}\), we have
\begin{align*} 2-2 \cdot \cos\left(\alpha -\beta \right) & = 2-2\left(\cos\alpha\cos \beta +\sin\alpha \sin\beta \right) \\ 2 \cdot \cos\left(\alpha -\beta \right) & = 2\left(\cos\alpha\cos \beta +\sin\alpha \sin\beta \right) \\ \therefore \cos\left(\alpha -\beta \right) & = \cos \alpha \cos\beta +\sin\alpha \sin\beta \end{align*}Derive an expression for \(\cos\left(\alpha + \beta \right)\) in terms of the trigonometric ratios of \(\alpha\) and \(\beta\).
We use the compound angle formula for \(\cos \left(\alpha - \beta \right)\) and manipulate the sign of \(\beta\) in \(\cos \left(\alpha + \beta \right)\) so that it can be written as a difference of two angles:
\begin{align*} \cos (\alpha + \beta ) & = \cos (\alpha - (-\beta )) \\ \text{And we have shown } \cos (\alpha - \beta )& = \cos \alpha \cos\beta +\sin\alpha \sin\beta \\ \therefore \cos [\alpha - (- \beta )]& = \cos \alpha \cos(-\beta) +\sin\alpha \sin(-\beta) \\ \therefore \cos (\alpha + \beta ) & = \cos \alpha \cos\beta - \sin\alpha \sin \beta \end{align*}Derive the expanded formulae for \(\sin\left(\alpha - \beta \right)\) and \(\sin\left(\alpha + \beta \right)\) in terms of the trigonometric ratios of \(\alpha\) and \(\beta\).
Using co-functions, we know that \(\sin \hat{A} = \cos ( \text{90} ° - \hat{A} )\), so we can write \(\sin \left(\alpha + \beta \right)\) in terms of the cosine function as:
\begin{align*} \sin ( \alpha - \beta ) & = \cos \left( \text{90} ° - ( \alpha - \beta ) \right) \\ & = \cos \left( \text{90} ° - \alpha + \beta \right) \\ & = \cos \left[ ( \text{90} ° - \alpha) + \beta \right] \end{align*}Apply the compound angle formula:
\begin{align*} \cos (\alpha + \beta ) & = \cos \alpha \cos\beta - \sin\alpha \sin\beta \\ \therefore \cos \left[ ( \text{90} ° - \alpha) + \beta \right] & = \cos ( \text{90} ° - \alpha) \cos\beta - \sin ( \text{90} ° - \alpha) \sin\beta \\ \therefore \sin( \alpha - \beta) & = \sin \alpha \cos\beta - \cos \alpha \sin\beta \end{align*}To derive the formula for \(\sin ( \alpha + \beta )\), we use the compound formula for \(\sin ( \alpha - \beta )\) and manipulate the sign of \(\beta\):
\begin{align*} \sin (\alpha - \beta )& = \sin \alpha \cos\beta - \cos \alpha \sin\beta \\ \text{We can write } \sin ( \alpha + \beta ) & = \sin \left[ \alpha - (- \beta ) \right] \\ \therefore \sin \left[ \alpha - (- \beta ) \right] &= \sin \alpha \cos (-\beta) - \cos \alpha \sin (-\beta) \\ \therefore \sin ( \alpha + \beta ) & = \sin \alpha \cos\beta + \cos \alpha \sin\beta \end{align*}Compound angle formulae
Note: we can use the compound angle formulae to expand and simplify compound angles in trigonometric expressions (using the equations from left to right) or we can use the expanded form to determine the trigonometric ratio of a compound angle (using the equations from right to left).
Prove that \(\sin \text{75} °=\frac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}\) without using a calculator.
We know the values of the trigonometric functions for the special angles ( \(\text{30}\) °, \(\text{45}\) °, \(\text{60}\) °, etc.) and we can write \(\text{75} ° = \text{30} ° + \text{45} °\).
Therefore, we can use the compound angle formula for \(\sin (\alpha + \beta )\) to express \(\sin \text{75} °\) in terms of known trigonometric function values.
When proving an identity is true, remember to only work with one side of the identity at a time.
\begin{align*} \text{LHS }& = \sin \text{75} ° \\ & = \sin \left( \text{45} °+ \text{30} °\right) \\ \sin \left( \text{45} °+ \text{30} °\right) & = \sin \left( \text{45} ° \right)\cos\left( \text{30} ° \right)+\cos\left( \text{45} ° \right)\sin\left( \text{30} ° \right) \\ & = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{3}}{2}+\frac{1}{\sqrt{2}} \cdot \frac{1}{2} \\ & = \frac{\sqrt{3}+1}{2\sqrt{2}} \\ & = \frac{\sqrt{3}+1}{2\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}} \\ & = \frac{\sqrt{2}\left(\sqrt{3}+1\right)}{4} \\ &= \text{RHS} \end{align*}Therefore, we have shown that \(\sin{75}°=\frac{\sqrt{2}\left(\sqrt{3}+1\right)}{4}\).
Determine the value of the following expression without the use of a calculator:
\[\cos \text{65} ° \cos \text{35} ° + \cos \text{25} ° \cos \text{55} °\]Checking answers: It is always good to check answers. The question stated that we could not use a calculator to find the answer, but we can use a calculator to check that the answer is correct:
\begin{align*} \text{LHS}&= \cos \text{65} ° \cos \text{35} ° + \cos \text{25} ° \cos \text{55} ° = \text{0,866} \ldots \\ \text{RHS}&= \frac{\sqrt{3}}{2} = \text{0,866} \ldots \\ \therefore \text{LHS} &= \text{RHS} \end{align*}Given:
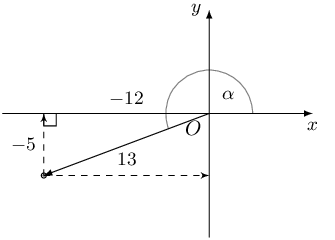
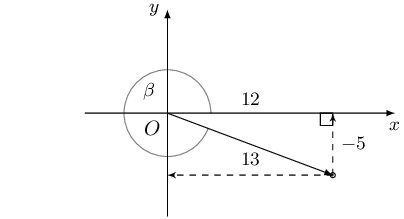
\[\begin{array}{rll} 13 \sin \alpha+ 5 &= 0 & ( \text{0} ° < \alpha< \text{270} ° ) \\ 13 \cos \beta - 12 &= 0 & ( \text{90} ° < \beta < \text{360} ° ) \end{array}\]Draw a sketch and determine the following, without the use of a calculator:


Calculate the following without the use of a calculator (leave answers in surd form):
We have shown that:
\begin{align*} \sin ( \text{60} ° - x) + \sin ( \text{60} ° + x) &= \sqrt{3} \cos x \\ \text{If we let } x &= \text{45} ° \\ \sin ( \text{60} ° - \text{45} °) + \sin ( \text{60} ° + \text{45} °) &= \sqrt{3} \cos \text{45} ° \\ \sin \text{15} ° + \sin \text{105} ° &= \sqrt{3} \cdot \frac{1}{\sqrt{2}} \\ &= \frac{\sqrt{3}}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} \\ &= \frac{\sqrt{6}}{2} \end{align*}For \(x = \text{45} °\):
\begin{align*} \text{LHS}&= \sin \text{15} ° + \sin \text{105} ° \\ &= \text{1,2247} \ldots \\ \text{RHS} &= \text{1,2247} \ldots \\ \therefore \text{LHS} &= \text{RHS} \end{align*}Simplify the following without using a calculator:
\[\frac{\sin p \cos( \text{45} ° - p) + \cos p \sin( \text{45} ° - p)}{\cos p \cos( \text{60} ° - p) - \sin p \sin( \text{60} ° - p)}\]We have shown that:
\begin{align*} 2 \cos A \sin B &= \sin (A + B) - \sin (A -B) \\ \therefore \cos A \sin B &= \frac{1}{2} \left( \sin (A + B) - \sin (A -B) \right) \\ \text{Let } A &= \text{75} ° \\ \text{And let } B &= \text{15} ° \\ \cos \text{75} ° \sin \text{75} ° &= \frac{1}{2} \left( \sin ( \text{75} ° + \text{15} °) - \sin ( \text{75} ° - \text{15} °) \right) \\ &= \frac{1}{2} \left( \sin \text{90} ° - \sin \text{60} ° \right) \\ &= \frac{1}{2} \left( 1 - \frac{\sqrt{3}}{2} \right) \\ &= \frac{2 - \sqrt{3}}{4} \end{align*}In the diagram below, points \(P\) and \(Q\) lie on the circle with radius of \(\text{2}\) units and centre at the origin.
Prove \(\cos (\theta - \beta) = \cos \theta \cos \beta + \sin \theta \sin \beta\).
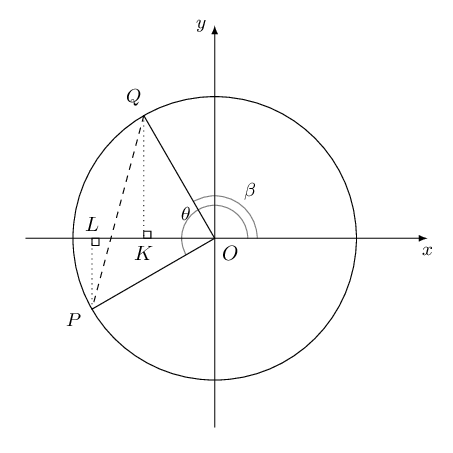
We can express the coordinates of \(P\) and \(Q\) in terms of the angles \(\theta\) and \(\beta\):
\begin{align*} \text{For } Q: \quad \sin \beta &= \frac{y}{2} \\ \therefore y &= 2 \sin \beta \\ \text{and } x &= 2 \cos \beta \\ \therefore & Q(2 \cos \beta; 2 \sin \beta) \\ & \\ \text{Similarly, } & P(2 \cos \theta; 2 \sin \theta) \end{align*}We use the distance formula to determine \(PQ^{2}\):
\begin{align*} \text{In } & \triangle POQ, \\ P\hat{O}Q &= \theta - \beta \\ {d}^{2} &= {\left({x}_{P}-{x}_{Q}\right)}^{2}+{\left({y}_{P}-{y}_{Q}\right)}^{2} \\ PQ^{2}& = {\left(2\cos\theta -2\cos\beta \right)}^{2}+{\left(2\sin\theta -2\sin\beta \right)}^{2} \\ & = 4{\cos}^{2}\theta -8\cos\theta\cos \beta +4{\cos}^{2}\beta +4{\sin}^{2}\theta -8\sin\theta\sin \beta +4 {\sin}^{2}\beta \\ & = 4\left({\cos}^{2}\theta +{\sin}^{2}\theta \right)+4\left({\cos}^{2}\beta +{\sin}^{2}\beta \right)-8\cos\theta\cos \beta -8\sin\theta\sin \beta \\ & = 8 -8 \left(\cos\theta\cos \beta +\sin\theta\sin \beta \right) \end{align*}Now we determine \(PQ^{2}\) using the cosine rule for \(\triangle POQ\):
\begin{align*} PQ^{2}& = {2}^{2}+{2}^{2}-2\left(2\right)\left(2\right)\cos\left(\theta -\beta \right) \\ & = 8 -8 \cos\left(\theta -\beta \right) \end{align*}Equating the two expressions for \(PQ^{2}\), we have
\begin{align*} 8 - 8 \cos\left(\theta -\beta \right) & = 8 - 8\left(\cos\theta\cos \beta +\sin\theta \sin\beta \right) \\ \therefore \cos\left(\theta -\beta \right) & = \cos \theta \cos\beta +\sin\theta \sin\beta \end{align*}Note: earlier in this chapter we derived the compound angle identities using a unit circle (radius = \(\text{1}\) unit) because it simplified the calculations. From the exercise above, we see that the compound angle identities can in fact be derived using a radius of any length.
|
Previous
4.1 Revision
|
Table of Contents |
Next
4.3 Double angle identities
|