7.4 Working with equations, tables and flow diagrams
You have worked with flow diagrams, tables, and equations to find the missing numbers in Chapter 5. Now we will consolidate the work and see how to find solutions to the given equation.
Worked Example 7.18: Working with equations and a table
The table below summarises the equation \(y = 6x + 3\). However, there is a missing number in the \(y\)-values.
| \(x\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y\) | \(15\) | \(21\) | \(?\) | \(33\) | \(39\) |
- What is the missing number?
- Find a solution to the equation \(15 = 6x + 3\).
Calculate the missing value.
This question asks us to find one of the \(y\)-values for the equation \(y = 6x + 3\). In order to do this calculation, we must find the correct input value to use. From the table we can get input value to use: \(x = 4\).
To find the corresponding output value, substitute \(x = 4\) into the equation. Then calculate the answer for \(y\).
Plug in \(x = 4\):
\[\begin{align} y &= 6x + 3 \\ y &= 6(4) + 3 \\ y &= 24 + 3 \\ y &= 27 \end{align}\]The missing value from the table is the output value of \(y = 27\).
Identify the correct pair of coordinates.
We have an equation, and we need to identify which ordered pair is a solution to the equation. Remember that a solution for the equation has values for \(x\) and \(y\) which fit into the equation.
The table in the question shows five solutions to the equation (including the one with the \(?\)): each pair of numbers in the table shows a pair of numbers that solve the equation.
The correct pair of numbers from the list is highlighted in the table below. This pair means that if we put \(x = 2\) into the equation \(15 = 6x + 3\), then we will get \(y = 15\) out.
| \(x\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y\) | \(15\) | \(21\) | \(?\) | \(33\) | \(39\) |
That is what it means to solve the equation: the two numbers work when you substitute them into the equation.
Worked Example 7.19: Working with equations and a flow diagram
The flow diagram below summarises the equation \(y = 2x\). However, there is a missing number in the output values.
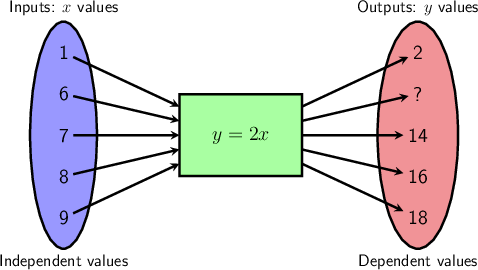
- What is the missing number?
- Write down the solutions to the equation \(y = 2x\) shown in the diagram.
Find the corresponding input value for the missing output value.
This question asks us to find one of the output values for the equation \(y = 2x\). In order to do this calculation, we must find the correct input value to use. From the flow diagram we can get input value to use: \(x = 6\).
Calculate the missing value.
To calculate the corresponding output value, substitute \(x = 6\) into the equation. Then calculate the answer for \(y\).
If \(x = 6\):
\[\begin{align} y &= 2x \\ y &= 2(6) \\ &= 12 \end{align}\]The missing value from the diagram is the output value of \(y = 12\).
Find all the solutions from the flow diagram.
Remember that a solution for the equation has values for \(x\) and \(y\) that fit into the equation.
The flow diagram in the question shows five solutions to the equation (including the one with the \(?\)). Each pair of numbers in the flow diagram shows a pair of numbers that solve the equation.
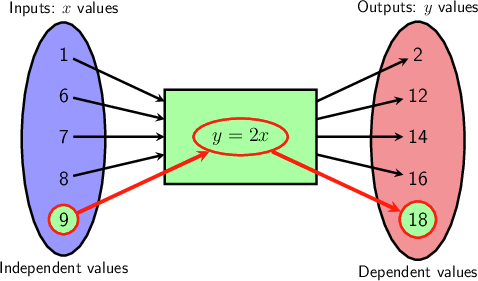
The pairs of numbers from the flow diagram will give the solutions of the equation. For example, the pair \((9; 18)\) is a solution, which means that if we put \(x = 9\) into the equation, then we will get \(y = 18\) out. That is what it means to solve the equation: the two numbers work when you substitute them into the equation.
So, the following pairs solve the equation: \((1;2), (6;12), (7;14), (8;16), (9;18)\).
There are many more pairs of numbers that solve the equation \(y = 2x\). In fact, there are an infinitely many solutions for this equation, because there are an infinite number of numbers to use as inputs and outputs!
