22.5 Solving problems
Knowing how to set up and solve equations will help you solve real-world problems. It helps to break the word problems down, separate the knowns and unknowns, and then transform the words and numbers into mathematical equations.
These steps will help you:
- Read the problem carefully.
- Write down what you know and what you don’t know.
- Assign variables to the unknowns and set up the equation.
- Solve the equation.
- Reflect on the answer to check that it seems reasonable.
- Give the answer as a sentence.
Worked Example 22.6: Calculating costs
Last Friday, Sifiso went to the movies with his friends. He bought chips and sweets to eat while he was there. The sweets cost \(\text{R} 13\) more than the chips, and the movie ticket cost twice what the sweets cost.
Let the cost of the chips be \(c\) rand.
- Write an expression for the cost of the sweets, in terms of \(c\).
- Write a simplified expression for the cost of the movie ticket, in terms of \(c\).
- If the total cost of Sifiso’s night at the movies was \(\text{R} 99\), use an equation to calculate the cost of the chips.
Write an expression for the cost of the sweets.
The chips cost \(c\), and the sweets costs \(\text{R} 13\) more than the chips. We must add \(13\) to \(c\).
\[\begin{align} \text{cost of sweets} &= \text{cost of chips} + 13 \\ &= c + 13 \end{align}\]Write an expression for the cost of the movie.
The movie ticket cost twice what the sweets cost. We must multiply the expression for the cost of sweets by \(2\).
\[\begin{align} \text{cost of movie} &= 2 \times (\text{cost of sweets}) \\ &= 2 \times (c + 13) \\ &= 2c + 26 \end{align}\]Set up an equation to work out the cost of the chips.
We were told that the total cost of the outing was \(\text{R} 99\). This means that if we add together the costs of the chips, the sweets, and the movie, it will come to \(\text{R} 99\).
\[\begin{align} \text{chips} + \text{sweets} + \text{movie} &= 99 \\ c + (c + 13) + (2c + 26) &= 99 \end{align}\]Solve the equation.
\[\begin{align} c + (c + 13) + (2c + 26) &= 99 \\ 4c + 39 &= 99 \\ 4c + 39 - 39 &= 99 - 39 \\ 4c &= 60 \\ \frac{4c}{4} &= \frac{60}{4} \\ \therefore c &= 15 \end{align}\]Reflect on the answer to check that it is reasonable.
\(\text{R} 15\) seems a reasonable answer for a packet of chips, if the sweets cost \(\text{R} 13\) more than the chips.
Give the answer as a sentence.
The chips cost \(\text{R} 15\).
Worked Example 22.7: Calculating temperature
Lesego is conducting an experiment in which the temperature of a solution is measured carefully. The temperature is \(111^{\circ}\) at the end of the first minute, and then it falls by \(4^{\circ}\) every minute after that.
- Determine a formula to calculate the temperature (\(T\)) after \(m\) minutes.
- After how many minutes will the temperature in the experiment be equal to \(−41^{\circ}\)?
Write out the first few terms of the pattern.
We know that the temperature is \(111^{\circ}\) at the end of the first minute, and then it falls by \(4^{\circ}\) every minute after that. We can represent the first few terms of the pattern in a table:
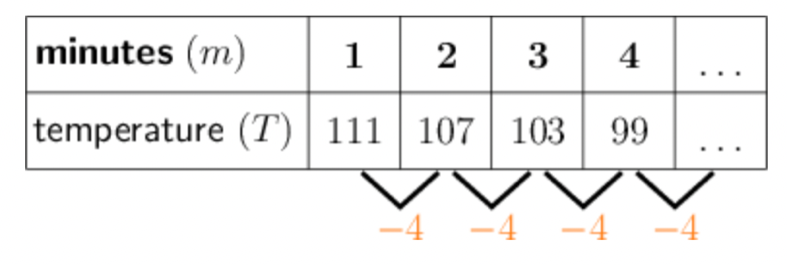
The pattern has a constant difference of \(−4\), so it is a linear pattern.
Determine the formula.
Linear patterns always have a formula that includes the term number multiplied by the constant difference, as well as a constant term.
Therefore, we know that this pattern has the formula \(T = - 4m + \square\). We still need to determine the value of the unknown constant term.
To determine the value of the constant term, we will look at the first term.
We know that the value of the first term is \(111\) (the temperature is \(111^{\circ}\) at the end of the first minute).
So we have:
\[\begin{align} 111 &= - 4 \times 1 + \square \\ \therefore 111 &= - 4 + \square \\ \therefore\ \square &= 115 \end{align}\]Therefore, the formula is \(T = - 4m + 115\).
Use the formula from Step 2.
In Step 2, we determined that the formula for the temperature after \(m\) minutes is \(T = - 4m + 115\). We will substitute \(−41\) for the temperature and solve for \(m\).
\[\begin{align} T &= - 4m + 115 \\ - 41 &= - 4m + 115 \\ - 156 &= - 4m \\ m &= \frac{- 156}{- 4} \\ \therefore m &= 39 \end{align}\]Reflect on the answer to check that it is reasonable.
\(39\) minutes seems reasonable for the number of minutes.
Give the answer as a sentence.
The temperature will be equal to \(- 41^{\circ}\) after \(39\) minutes.
Worked Example 22.8: Calculating proportion
Livhu, Rofhiwa, and Humbu shared a packet of sweets.
- Livhu ate five fewer than Rofhiwa.
- Humbu ate three times more than Livhu and Rofhiwa combined.
- Altogether, they ate \(28\) sweets.
How many sweets did Rofhiwa eat?
Choose the unknown variable.
Let the number of sweets eaten by Rofhiwa be \(r\).
Express each person’s quantity in terms of \(r\).
Write Livhu’s sweets in terms of \(r\):
We are told that Livhu eats five fewer than Rofhiwa. This means that
\[\begin{align} \text{Livhu's sweets} &= \text{Rofhiwa's sweets} - 5 \\ &= r - 5 \end{align}\]Write Humbu’s sweets in terms of \(r\):
We also know that Humbu eats three times more than Livhu and Rofhiwa combined. This means that we have to add Livhu and Rofhiwa’s sweets, and then multiply this by \(3\).
\[\begin{align} \text{Humbu's sweets} &= 3 \times \left(\text{Livhu's sweets} + \text{Rofhiwa's sweets} \right) \\ &= 3 \times (r - 5 + r) \\ &= 3 \times (2r - 5) \\ &= 6r - 15 \end{align}\]Write the total number of sweets in terms of \(r\).
We are told that Livhu, Rofhiwa, and Humbu eat \(28\) sweets in total. This means that if we add together the number of sweets of all three people, we will get \(28\).
\[\begin{align} \text{Livhu's sweets} + \text{Rofhiwa's sweets} + \text{Humbu's sweets} &= 28 \\ (r - 5) + r + (6r - 15) &= 28 \\ 8r - 20 &= 28 \\ 8r - 20 + 20 &= 28 + 20 \\ 8r &= 48 \\ \frac{8r}{8} &= \frac{48}{8} \\ \therefore r &= 6 \end{align}\]Reflect on the answer to check that it is reasonable.
Work out how many sweets each person ate and add:
- Livhu: \(r - 5 = 6 - 5 = 1\)
- Humbu: \(6r - 15 = 36 - 15 = 21\)
- Rofhiwa: \(6\)
The answer is correct.
Give the answer as a sentence.
Rofhiwa ate six sweets.
Worked Example 22.9: Calculating with data bundles
Abraham uses the internet on his cellphone for homework assignments. This uses up data, which can be used in-bundle or out-of-bundle. Abraham’s cellphone network charges different rates for in-bundle and out-of-bundle data usage.
Last week, he used \(44 \text{ MB}\) of data in-bundle, and \(6 \text{ MB}\) of data out-of-bundle. Out-of-bundle data costs \(\text{R} \text{1,50}\) more than twice the cost of in-bundle data, per \(\text{MB}\).
Let the cost of in-bundle data (per \(\text{MB}\)) be \(z\).
- Write an expression for the cost of out-of-bundle data (per \(\text{MB}\)), in terms of \(z\).
- Abraham paid \(\text{R} \text{109,80}\) for his data last week. (He got into big trouble with his mom.) Use an equation to calculate the cost of both in-bundle and out-of-bundle data, per \(\text{MB}\).
Write an expression for the cost of out-of-bundle data.
Out-of-bundle data costs \(\text{R} \text{1,50}\) more than twice the cost of in-bundle data, per \(\text{MB}\). We must add \(\text{R} \text{1,50}\) to the product of \(2\) and \(z\).
\[\begin{align} & \text{out-of-bundle data cost (per MB)} \\ & = 2 \times (\text{cost of in-bundle data}) + \text{1,5} \\ & = 2 \times (z) + \text{1,5} \\ & = 2z + \text{1,5} \end{align}\]Set up the equation.
Abraham’s total data costs are the sum of the amounts spent on in-bundle data and out-of-bundle data. To work out the amount spent on each type of data, we must multiply the number of \(\text{MBs}\) used by the cost of that type of data.
Last week’s in-bundle costs:
\[\begin{align} \text{cost} &= \text{number of MBs} \times \text{cost per MB} \\ &= 44 \times z \\ &= 44z \end{align}\]Last week’s out-of-bundle costs:
\[\begin{align} \text{cost} &= \text{number of MB} \times \text{cost per MB} \\ &= 6 \times (2z + \text{1,5}) \\ &= 12z + 9 \end{align}\]We can now use this information to set up an equation.
\[\begin{align} \text{total costs} &= \text{in-bundle costs} + \text{out-of-bundle costs} \\ \therefore \text{109,8} &= 44z + (12z + 9) \end{align}\]Solve the equation.
\[\begin{align} \text{109,8} &= 44z + (12z + 9) \\ \text{109,8} &= 56z + 9 \\ \text{109,8} - 9 &= 56z + 9 - 9 \\ \text{100,8} &= 56z \\ \frac{\text{100,8}}{56} &= \frac{56z}{56} \\ \therefore \text{1,8} &= z \end{align}\]In-bundle data costs \(\text{R} \text{1,80}\) per \(\text{MB}\).
Calculate the cost of out-of-bundle data.
The question also asks for the cost of out-of-bundle data, per \(\text{MB}\). We can use the value of \(z\), and the expression that we set up in Step 1.
\[\begin{align} \text{cost of out-of-bundle data (per MB)} &= 2z + \text{1,5} \\ &= 2(\text{1,8}) + \text{1,5} \\ &= \text{3,6} + \text{1,5} \\ &= \text{5,1} \end{align}\]Give the answer as a sentence.
Out-of-bundle data costs \(\text{R} \text{5,10}\) per \(\text{MB}\).
