6.5 Using laws to simplify expressions
Distributive law
To “distribute” means to deliver or pass around. For example, before a test, the teacher must distribute the test paper to each student in the class. Recall the distributive property of multiplication over addition (or subtraction):
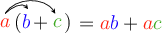
We also call the distributive property the distributive law.
For example, we use the distributive law to multiply out the following:
\[5(y - 6)\]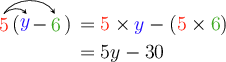
We can’t simplify \(5y - 30\) any further, because \(5y\) and \(- 30\) are not like terms.
Worked example 6.17: Distributive law
Distribute in order to expand this expression: \(5(10 + g)\)
Apply the distributive law:
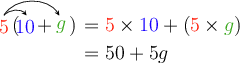
Commutative law
Remember the commutative property of multiplication:
\[a \times b = b \times a\]For example, \(3 \times 5 = 5 \times 3\).
We also call the commutative property the commutative law.
Worked example 6.18: Distributive and commutative law
Expand the following expression by multiplying out the brackets:
\[(7x - 3)5\]Use the commutative law.
\[(7x - 3)5 = 5(7x - 3)\]Apply the distributive law.
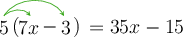
Worked example 6.19: Simplify trinomials
Distribute in order to expand this expression:
\[5(4f^{2} + 2f + 5)\]Apply the distributive law.
For the expression \(5(4f^{2} + 2f + 5)\), you must distribute the 5 to all three of the terms in the brackets.
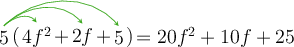
Remember, to simplify an expression:
- separate it into terms
- simplify each term (if needed)
- add or subtract like terms from left to right.
Worked example 6.20: Simplify expressions with like terms
Simplify the following expression:
\[5 + 2(5n - 7)\]Separate the expression into terms.
\(5 + 2(5n - 7)\) has two terms: \(5\) and \(+ 2(5n - 7)\).
Simplify using the distributive law.
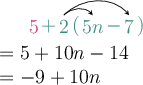
Adding and subtracting algebraic terms
We have already come across the commutative and associative laws of operations. We will now use these laws to help us form equivalent algebraic expressions.
- Commutative law: The order in which we add or multiply numbers does not change the
answer:
\(a + b = b + a\) and \(ab = ba\). - Associative law: The way in which we group three or more numbers when adding or multiplying
does not change the answer:
\((a + b) + c = a + (b + c)\) and \((ab)c = a(bc)\).
Worked example 6.21: Adding algebraic terms
Add \(5r^{2} + 5r - 4\) to \(4r^{2} - r\).
Write and simplify the expression.
We must start with \(4r^{2} - r\) and add \(5r^{2} + 5r - 4\) to it.
\[\left( 4r^{2} - r \right) + \left( 5r^{2} + 5r - 4 \right)\] \[= 4r^{2} - r + 5r^{2} + 5r - 4\] \[= 9r^{2} + 4r - 4\]\[+ \ (5r^{2} + 5r - 4)\ = + 1(5r^{2} + 5r - 4)\]When we distribute in \(+1\), the signs don’t change.
Worked example 6.22: Subtracting algebraic terms
Subtract \(4r - t\) from \(5r + 5t - 4\).
Write and simplify the expression.
We must start with \(5r + 5t - 4\) and subtract \(4r - t\) from it.
\[(5r + 5t - 4) - (4r - t)\] \[= 5r + 5t - 4 - 4r + t\] \[= r + 6t - 4\]\[- (4r - t)\ = - 1(4r - t)\]When we distribute in the \(−1\), all the signs change!
