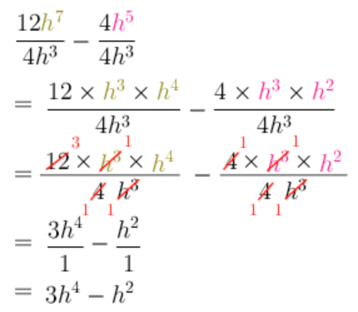8.2 Operations with algebraic expressions
You have learnt about terms in algebraic expressions. Let’s look at some new terminology that we will use in this chapter. An algebraic expression that has:
- only one term is called a monomial
- two terms is called a binomial
- three terms is called a trinomial.
- monomial
- an algebraic expression that has one term
- binomial
- an algebraic expression that has two terms
- trinomial
- an algebraic expression that has three terms
Multiplying and dividing monomials
When multiplying or dividing one monomial by another, and both have constants and variables, we use the laws of exponents. The laws of multiplication and division of exponents, as well as raising to a power will be very handy in this chapter:
- \(a^{m} \times a^{n} = a^{m + n}\)
- \(\frac{a^{m}}{a^{n}} = a^{m - n}\)
- \(\left(a^{m} \right)^{n} = a^{mn}\)
These laws also apply to more than one monomial. For example:
\[\begin{align} x^{2} \times x^{4} \times x^{6} &= x^{2 + 4 + 6} \\ &= x^{12} \end{align}\]and
\[\begin{align} \frac{y^{3} \times y^{5}}{y^{4}} &= \frac{y^{3 + 5}}{y^{4}} \\ &= \frac{y^{8}}{y^{4}} \\ &= y^{8 - 4} \\ &= y^{4} \end{align}\]If there are different bases and constant factors in the algebraic expressions, follow these rules of multiplication and division:
- Multiply the constant factors, and multiply the powers of the same base.
- Divide the constant factors, and divide the powers of the same base.
Worked Example 8.1: Multiplying algebraic monomials
Simplify the following expression:
\[\left(- 3r^{2} \right) \times ( - 4t) \times t^{3} \times 3r^{4}\]Regroup the expression.
We must group the constant factors together and the same variables together:
\[\begin{align} &\left(- 3r^{2} \right) \times (- 4t) \times t^{3} \times 3r^{4} \\ =&\ (- 3) \times (- 4) \times 3 \times r^{2} \times r^{4} \times t \times t^{3} \end{align}\]Multiply the constant factors, and multiply the powers of the same base.
\[\begin{align} &( - 3) \times ( - 4) \times 3 \times r^{2} \times r^{4} \times t \times t^{3} \\ =&\ 36 \times r \times r \times r \times r \times r \times r \times t \times t \times t \times t \\ =&\ 36r^{6}t^{4} \end{align}\]Exponents tell us how many times to multiply a base.
When we multiply powers of the same base, we can add the exponents:
\[\begin{align} &\left( - 3r^{2} \right) \times ( - 4t) \times t^{3} \times 3r^{4} \\ =&\ 36 \times r^{2 + 4} \times t^{1 + 3} \\ =&\ 36r^{6}t^{4} \end{align}\]
Worked Example 8.2: Dividing algebraic monomials
Simplify the following expression:
\[24t^{7} \div 4t^{5}\]Rewrite the division as a fraction.
We can write division as a fraction: \(a \div b = \frac{a}{b}\).
This question is written with a division symbol (\(\div\)), but this is the same as writing it as a fraction:
\[24t^{7} \div 4t^{5} = \frac{24t^{7}}{4t^{5}}\]Expand the powers.
We will group the numbers together, and the powers of the same base together, and see what we can simplify.

Algebraic fractions
The algebraic expressions that involve division are called algebraic fractions. The rules that govern operations with fractions also apply to algebraic fractions.
Here are some important things to remember about fractions:
- When multiplying fractions, we multiply the numerators and multiply the denominators: \(\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\).
- So, we can also go the opposite way to separate the fraction when we have a fraction with only products: \(\frac{a \times c}{b \times d} = \frac{a}{b} \times \frac{c}{d}\)
- When we divide any number by itself, other than zero, we get \(1\). For example, \(\frac{5}{5} = 1\). Therefore, \(\frac{a}{a} = 1\) (as long as \(a\) is not equal to zero).
Worked Example 8.3: Simplifying algebraic fractions
Simplify the following expression:
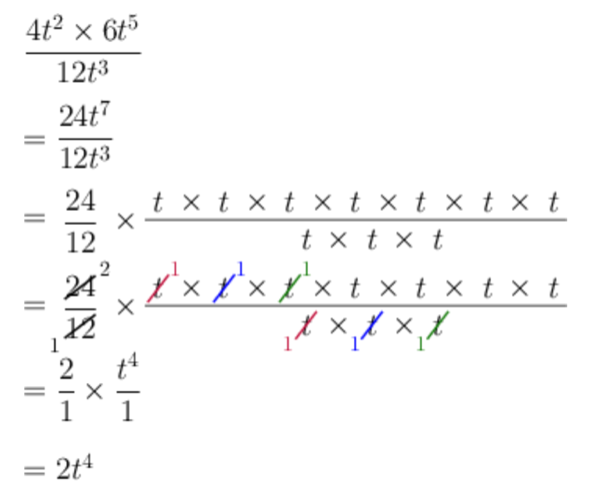
\[\frac{4t^{2} \times 6t^{5}}{12t^{3}}\]Simplify the numerator and the denominator.
We have a product in the numerator, so we group constants and variables:
\[\begin{align} & 4t^{2} \times 6t^{5} \\ = &\ 4 \times 6 \times t^{2} \times t^{5} \\ = &\ 24 \times t^{2 + 5} \\ = &\ 24t^{7} \end{align}\]The denominator doesn’t need to be simplified: \(12t^{3}\).
Expand the powers.
We will group the numbers together, and the powers of the same base together, and see what we can simplify.
Worked Example 8.4: Simplifying algebraic fractions
Simplify the following expression:
\[\frac{10w^{3}y^{3}}{25wy^{3}}\]Then evaluate the expression for \(w = 3\) and \(y = 9\).
Expand the powers.
We will group the numbers together, and the powers of the same base together, and see what we can simplify.

When dividing powers of the same base, we can subtract the exponents:
- If the coefficient in the numerator is larger: \(\frac{x^{m}}{x^{n}} = x^{m - n}\)
- If the coefficient in the denominator is larger: \(\frac{x^{m}}{x^{n}} = \frac{1}{x^{n - m}}\)
Use the simplified expression and substitute.
In Step 1, we determined that \(\frac{10w^{3}y^{3}}{25wy^{3}}\) is equal to \(\frac{2w^{2}}{5}\). Therefore, we can substitute \(w = 3\) into the simplified expression:
\[\begin{align} \frac{10w^{3}y^{3}}{25wy^{3}} & = \frac{2w^{2}}{5} \\ & = \frac{2(3)^{2}}{5} \\ & = \frac{2 \times 9}{5} \\ & = \frac{18}{5} \end{align}\]The variable \(y\) cancelled out in the simplification. So, the value of the expression does not depend on the value of \(y\). If you want to, you can subsitute the values of \(y\) and \(w\) into the original expression. You will get the same answer, but it will be a lot more work to calculate.
When working with algebraic fractions, you can also be asked to add or subtract them. Or you might even need to do all operations in the same algebraic expression.
To simplify an expression:
- Separate it into terms. Terms are separated by addition and subtraction symbols, and joined into one by multiplication and division symbols, and brackets.
- Simplify each term (if needed).
- Add or subtract like terms from left to right (if possible).
Remember, just like with common fractions, when adding or subtracting algebraic fractions, you will often need to find the common denominator.
When adding (or subtracting) fractions, if the denominators are the same, then we can add (or subtract) the numerators: \(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\).
So, we can also go the opposite way to separate the fraction when we have a fraction with addition (or subtraction) in the numerator: \(\frac{a + b}{c} = \frac{a}{c} + \frac{b}{c}\).
Worked Example 8.5: Adding and subtracting algebraic fractions
Simplify the following expression:
\[\frac{12h^{7}}{4h^{3}} - \frac{4h^{5}}{4h^{3}}\]Each fraction is its own term. This expression has two terms, so it is a binomial.
We will simplify each fraction, then see if we can add the results.
Simplify the first fraction.
\[\begin{align} \frac{12h^{7}}{4h^{3}} &= \frac{12}{4} \times \frac{h^{7}}{h^{3}} \\ &= 3h^{7 - 3} \\ &= 3h^{4} \end{align}\]Simplify the second fraction.
\[\begin{align} \frac{4h^{5}}{4h^{3}} &= \frac{4}{4} \times \frac{h^{5}}{h^{3}} \\ &= 1h^{5 - 3} \\ &= h^{2} \end{align}\]Subtract the answers.
\[3h^{4} - h^{2}\]We can’t add \(3h^{4}\) and \(- h^{2}\), because they are not like terms (they do not have exactly the same base and exponent).
You do not need to do simplifications step by step. You can simplify without writing out each fraction separately:
Mixed operations with algebraic fractions
Worked Example 8.6: Simplifying mixed operations with algebraic fractions
Simplify the following expression:
\[\frac{24g^{5} - 3g^{3} + 15g^{2}}{- 3g^{2}}\]Separate the fractions.
Since the denominator is negative, we must take extra care when dividing the coefficients to ensure that we get the correct signs.
\[\begin{align} &\frac{24g^{5} - 3g^{3} + 15g^{2}}{- 3g^{2}} \\ =&\ \frac{24g^{5}}{- 3g^{2}} - \frac{3g^{3}}{- 3g^{2}} + \frac{15g^{2}}{- 3g^{2}} \end{align}\]Simplify each fraction.
Use the exponents rule of division to simplify each fraction:
\[\begin{align} \frac{24g^{5}}{- 3g^{2}} &= \left( 24 \div ( - 3) \right) \times \left( g^{5 - 2} \right) \\ &= - 8g^{3} \end{align}\] \[\begin{align} \frac{3g^{3}}{- 3g^{2}} &= \left( 3 \div ( - 3) \right) \times \left( g^{3 - 2} \right) \\ &= - 1 \times g^{1} \\ &= - g \end{align}\] \[\begin{align} \frac{15g^{2}}{- 3g^{2}} &= \left( 15 \div ( - 3) \right) \times \left( g^{2 - 2} \right) \\ &= - 5 \times g^{0} \\ &= - 5 \times 1 \\ &= - 5 \end{align}\]Collect the terms.
\[\begin{align} & \frac{24g^{5}}{- 3g^{2}} - \frac{3g^{3}}{- 3g^{2}} + \frac{15g^{2}}{- 3g^{2}} \\ = & - 8g^{3} - ( - g) - 5 \\ = & - 8g^{3} + g - 5 \end{align}\]Worked Example 8.7: Simplifying mixed operations with algebraic fractions
Simplify the following expression:
\[2t^{3} + \frac{16t^{4} - 20t^{2} + 4t}{4t}\]Evaluate the expression if \(t = - 2\).
Separate the fraction term.
This expression has two terms. First, we will simplify the fraction term, then we will see if we can add any like terms.
\[\begin{align} & 2t^{3} + \frac{16t^{4} - 20t^{2} + 4t}{4t} \\ = &\ 2t^{3} + \left( \frac{16t^{4}}{4t} - \frac{20t^{2}}{4t} + \frac{4t}{4t} \right) \end{align}\]Simplify.
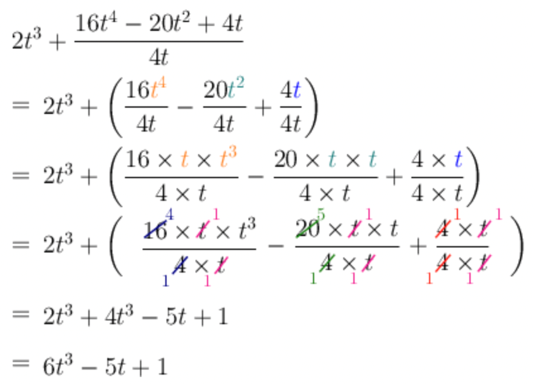
Evaluate the expression.
In Step 2, we determined that \(2t^{3} + \frac{16t^{4} - 20t^{2} + 4t}{4t}\) is equal to \(6t^{3} - 5t + 1\).
Therefore, we can substitute \(t = - 2\) into the simplified expression:
\[\begin{align} & 2t^{3} + \frac{16t^{4} - 20t^{2} + 4t}{4t} \\ = &\ 6t^{3} - 5t + 1 \\ = &\ 6( - 2)^{3} - 5( - 2) + 1 \\ = &\ 6( - 8) + 10 + 1 \\ = & - 48 + 10 + 1 \\ = & - 37 \end{align}\]Worked Example 8.8: Simplifying mixed operations with algebraic fractions
Simplify the following expression:
\[\frac{18t^{3} + \left( - 2t^{2} \right)^{3} - 10t^{4}}{2t^{2}}\]Simplify the term in the numerator within the brackets.
Exponents tell us how many times to multiply a base by itself.
We must treat the entire term within the brackets as the base. So, the base is \(- 2t^{2}\) and the exponent tells us to multiply this base by itself three times.
Separate the fractions.