8.4 Simplifying algebraic expressions
Distributive law
To distribute means to deliver or pass around. For example, before a test, the teacher must distribute the test paper to each learner in the class. Recall the distributive property of multiplication over addition (or subtraction):
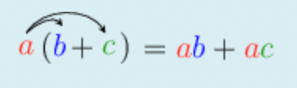
The distributive properties may be described as follows:
- \(a(b + c) = ab + ac\)
- \(a(b - c) = ab - ac\)
where \(a\), \(b\) and \(c\) can be any numbers.
We use this property when simplifying algebraic expressions. For example, to simplify \(5(y - 6)\), we follow these steps:
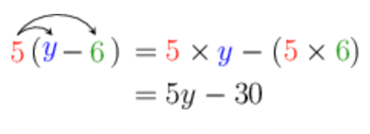
When evaluating an algebraic expression, the given value could be substituted into the expression before or after simplifying. The answer must be the same. For example, to determine the value of \(5(y - 6)\) if \(y = 9\), you substitute \(9\) into the expression:
\[\begin{align} 5(9 - 6) &= 5(3) \\ &= 15 \end{align}\]We can also substitute into the simplified expression:
\[\begin{align} 5(9) - 30 &= 45 - 30 \\ &= 15 \end{align}\]The process of writing product expressions as sum expressions is called expansion. It is sometimes also referred to as multiplication of algebraic expressions.
When you are not sure whether you simplified an expression correctly, you should always check your work by evaluating the original expression and the simplified expression for some values of the variables.
For example, we simplify \(x(x - 1) + 2x - 1\):
\[\begin{align} & x(x - 1) + 2x - 1 \\ &= x^{2} - x + 2x - 1 \\ &= x^{2} + x - 1 \end{align}\]Now, substitute any number, e.g. \(x = 1\), into the expression you were given and into the simplified expression:
\[\begin{align} & x(x - 1) + 2x - 1 \\ &= (1)(1 - 1) + 2(1) - 1 \\ &= 1(0) + 2 - 1 \\ &= 2 - 1 \\ &= 1 \end{align}\]and
\[\begin{align} & x^{2} + x - 1 \\ &= (1)^{2} + 1 - 1 \\ &= 1 + 1 - 1 \\ &= 1 \end{align}\]The answer is the same, so there is a good chance that we simplified correctly and \(x(x - 1) + 2x - 1 = x^{2} + x - 1\).
The substitution step doesn’t guarantee that the simplifications were done correctly, but it is a good step in checking the work.
Worked Example 8.15: Using the distributive law to simplify algebraic expressions
Simplify the following expression:
\[6(y - 5)\]Apply the distributive property.
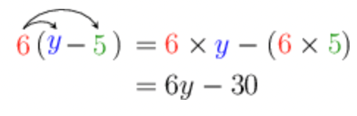
We can’t simplify \(6y - 30\) any further, because \(6y\) and \(- 30\) are not like terms.
Worked Example 8.16: Using the distributive law to simplify algebraic expressions
Expand the following expression by multiplying out the brackets:
\[- 2(y - 5)\]Apply the distributive property.
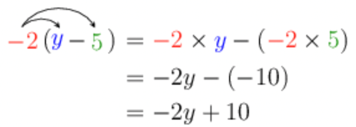
Don’t forget to distribute the negative to the second term!
Worked Example 8.17: Using the distributive law to simplify trinomials
Distribute in order to expand this expression:
\[5\left(4f^{2} + 2f + 5 \right)\]Apply the distributive law
For the expression \(5\left(4f^{2} + 2f + 5 \right)\), you must distribute the \(5\) to all three terms in the brackets.
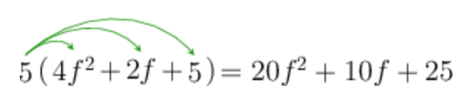
We can’t simplify any further because there are no like terms.
Adding, subtracting and simplifying algebraic expressions
Worked Example 8.18: Adding algebraic expressions
Add \(5r^{2} + 5r - 4\) to \(4r^{2} - r\).
Write the expression.
We must start with \(4r^{2} - r\) and add \(5r^{2} + 5r - 4\) to it.
\[\left( 4r^{2} - r \right) + \left( 5r^{2} + 5r - 4 \right)\]Simplify the expression.
\[\begin{align} & \left( 4r^{2} - r \right) + \left( 5r^{2} + 5r - 4 \right) \\ &= 4r^{2} - r + 5r^{2} + 5r - 4 \\ &= 9r^{2} + 4r - 4 \end{align}\]\[+ \left( 5r^{2} + 5r - 4 \right) = + 1(5r^{2} + 5r - 4)\]When we distribute \(+1\), the signs don’t change.
Worked Example 8.19: Subtracting algebraic expressions
Subtract \(4r - t\) from \(5r + 5t - 4\).
Write the expression.
We must start with \(5r + 5t - 4\) and subtract \(4r - t\) from it.
\[(5r + 5t - 4) - (4r - t)\]Simplify.
\[\begin{align} & (5r + 5t - 4) - (4r - t) \\ &= 5r + 5t - 4 - 4r + t \\ &= r + 6t - 4 \end{align}\]\[- (4r - t) = - 1(4r - t)\]When we distribute the \(−1\), all the signs change!
To simplify an expression:
- Separate it into terms. Terms are separated by addition and subtraction symbols, and joined into one by multiplication and division symbols, and brackets.
- Simplify each term (if needed).
- Add or subtract like terms from left to right.
Worked Example 8.20: Simplifying and collecting terms in algebraic expressions
Simplify the following by multiplying and collecting like terms:
\[- 9r + 3r(t + 3)\]Separate the expression into terms.
\(- 9r + 3r(t + 3)\) has two terms: \(- 9r\) and \(+ 3r(t + 3)\). We must simplify the second term using the distributive law, before collecting like terms.
Simplify using the distributive property.
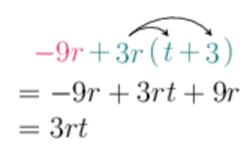
You might think that \(- 9r + 9r = 0r\). This is true! But, it is not fully simplified, because
\[0r = 0 \times r\]When we multiply any number by zero, we get zero.
Therefore, \(0r = 0\).
We always write \(0\) instead of \(0r\).
