18.3 Organise data
After data has been collected, the next step is to organise the data – that is, to bring it together in a systematic way that makes it easier to read. We can organise data by using tallies, frequency tables and stem-and-leaf diagrams. We can also group data into intervals.
Tallies
Tallies are a way of counting by drawing a short vertical line to record each item as you count it. To make reading the tally marks easier, for every fifth mark, you draw a diagonal line through the first four lines.
For example:
| Number | Description | Tally |
|---|---|---|
| \(8\) | \(1\) group of \(5\) and three vertical lines |  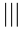 |
| \(12\) | \(2\) groups of \(5\) and two vertical lines |   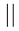 |
| \(15\) | \(3\) groups of \(5\) |    |
If we are given the tallies and have to find the number they represent, we count the groups of \(5\), then multiply the number of groups by \(5\) and add the individual strokes.
For example:
| Tally | Calculation | Answer |
|---|---|---|
 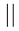 |
\((1 \times 5) + 2\) | \(5 + 2 = 7\) |
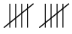 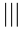 |
\((2 \times 5) + 3\) | \(10 + 3 = 13\) |
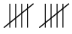 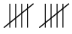  |
\((4 \times 5) + 4\) | \(20 + 4 = 24\) |
Frequency tables
When we have finished counting and adding up all the tally marks, the total number of tallies tell us how many times an event occurred. This is called the frequency.
- frequency
- how many times an event or observation occurred
A frequency table shows the list of different categories (for example, recyclable items), tallies for the number of times each item occurs, and the total number of tally marks.
For example:
The frequency table below shows the number of recycled items collected.
| Recyclable item | Tally | Frequency |
|---|---|---|
| Plastic bottle |  |
\(5\) |
| Cardboard box |  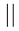 |
\(7\) |
| Tin can | 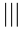 |
\(3\) |
| Glass bottle | 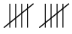 |
\(10\) |
So the frequency table shows that the frequency of plastic bottles was \(5\) and the frequency of glass bottles was \(10\).
Worked Example 18.2: Using tallies to complete a frequency table
The table shows the colours of cars parked outside a shopping centre.
| red | blue | white | blue | white |
| black | red | white | white | red |
| blue | white | black | white | white |
Use tallies to complete the frequency table.
| Colour | Tally | Frequency |
|---|---|---|
| Blue | ||
| Red | ||
| White | ||
| Black |
Use tallies to record the frequency of each colour of car in the parking lot.
Choose a method for reading and recording the data in the table. For example, you could read the data in each row from left to right or you could read the data in each column from top to bottom.
Be sure to keep to a regular approach so that you don’t miss any information.
| Colour | Tally | Frequency |
|---|---|---|
| Blue | 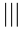 |
\(3\) |
| Red | 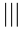 |
\(3\) |
| White |  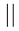 |
\(7\) |
| Black | 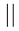 |
\(2\) |
Check that the sum of the frequencies equals the number of data points.
The number of data points in the set is the total number of items counted, in this case, it is the total number of cars. The data table has \(5\) columns and \(3\) rows, so there are \(5 \times 3 = 15\) data points.
It is good practice to make sure that the sum of the frequency column is equal to the number of data points in the set: \(3 + 3 + 7 + 2 = 15\).
Stem-and-leaf plots
A stem-and-leaf plot is a special representation of numerical data. Each data point is split into two parts; the stem part and the leaf part. The stem part determines the row in which the leaf part will be recorded. The leaf part is always a single digit.
For example:
- \(27\) can be split into \(2 \ \vert \ 7\) where \(2\) is the stem part and \(7\) is the leaf part.
- \(58\) can be split into \(5 \ \vert \ 8\) where \(5\) is the stem part and \(8\) is the leaf part.
- \(104\) can be split into \(10 \ \vert \ 4\) where \(10\) is the stem part and \(4\) is the leaf part. The leaf part is always a single digit, and here it is \(4\), so the leaf part must be \(10\).
Worked Example 18.3: Organising data in a stem-and-leaf plot
Represent the given data set as a stem-and-leaf plot.
\[45; 23; 86; 91; 42; 50; 12; 84; 47; 45; 22; 95; 39; 78; 69\]Record each data point on a stem-and-leaf plot.
In this data set, all the numbers have only two digits, so each stem will have one digit, and each leaf will have one digit.
Draw up your table starting with the stem numbers in your data set. In this data set, the stems are numbers \(1\) to \(9\).
Look for all the numbers in the data set that start with \(1\). There is only one, which is \(12\). Record that number with the stem \(1\) and the leaf \(1\).
Then look for all the numbers that start with \(2\). There are two numbers, \(23\) and \(22\). So you will have two numbers in the leaf column, \(3\) and \(2\).
Do the same for all the other numbers from \(3\) to \(9\).
| Stem | Leaf |
|---|---|
| \(1\) | \(2\) |
| \(2\) | \(3\) \(2\) |
| \(3\) | \(9\) |
| \(4\) | \(5\) \(2\) \(7\) \(5\) |
| \(5\) | \(0\) |
| \(6\) | \(9\) |
| \(7\) | \(8\) |
| \(8\) | \(6\) \(4\) |
| \(9\) | \(1\) \(5\) |
Arrange the leaf values in ascending order.
When we have recorded all the data points on the stem-and-leaf-plot, we arrange the leaf values in ascending order (from smallest value to largest) in each row.
| Stem | Leaf |
|---|---|
| \(1\) | \(2\) |
| \(2\) | \(2\) \(3\) |
| \(3\) | \(9\) |
| \(4\) | \(2\) \(5\) \(5\) \(7\) |
| \(5\) | \(0\) |
| \(6\) | \(9\) |
| \(7\) | \(8\) |
| \(8\) | \(4\) \(6\) |
| \(9\) | \(1\) \(5\) |
Check that the count of the leaf values equals the number of data points.
Make sure that the sum of the number of leaf values is equal to the number of data points in the data set:
\[1 + 2 + 1 + 4 + 1 + 1 + 1 + 2 + 2 = 15\]The data set has \(15\) data points.
Grouping data into intervals
We can also organise data by grouping data points into intervals (or classes). Intervals are a range of values that are consistently defined and equal in size. Intervals must not overlap, and there must be no gaps in the values between intervals.
The table below shows intervals of equal size in the first column. This is the correct method for defining the
number range of intervals.
The second column shows intervals that overlap, and intervals that are also different in size. This is not
correct.
| Example: Correctly defined intervals | Example: Incorrectly defined intervals |
|---|---|
| \(20–29\) | \(20–30\) |
| \(30–39\) | \(30–39\) |
| \(40–49\) | \(41–49\) |
Worked Example 18.4: Grouping data into intervals
Complete the frequency table for the given data set.
Recorded weights of baby rhinos (in kilograms):
\[42; 51; 45; 47; 46; 56; 51; 53; 59; 60; 62; 48; 49; 46; 41\]
| Baby rhino weight (kg) | Tally | Frequency |
|---|---|---|
| \(40–44\) | ||
| \(45–49\) | ||
| \(50–54\) | ||
| \(55–59\) | ||
| \(60–64\) |
Mark a tally for each data point and determine the frequency.
For each data point, identify the correct interval for the value of the data point and mark a tally in the appropriate row. When all the data points have been recorded, add up the tallies to determine the frequency.
| Baby rhino weight (kg) | Tally | Frequency |
|---|---|---|
| \(40–44\) | 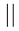 |
\(2\) |
| \(45–49\) | 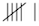 |
\(6\) |
| \(50–54\) | 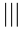 |
\(3\) |
| \(55–59\) | 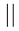 |
\(2\) |
| \(60–64\) | 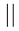 |
\(2\) |
Check that the sum of the frequencies equals the number of data points.
The data set has \(15\) data points.
Make sure that the sum of the frequency column is equal to the number of data points in the data set:
\[2 + 6 + 3 + 2 + 2 = 15\]