10.2 Construction instruments

A construction in mathematics is an accurate drawing of lines and angles. For most constructions, you should only use a pencil, a ruler and a pair of compasses.

1. A ruler. Use your ruler when you need to draw straight lines. Make sure the ruler is lined up accurately, and press down firmly on the ruler so that it does not move when drawing the line. When drawing a line of a specific length, use the markings on the ruler to be as accurate as possible.
   
2. A pair of compasses is an instrument for drawing circles. It can also be called “a compass”. A compass has a hinge that allows the width of the legs to be adjusted. A compass has two legs:
   • One leg has a sharp point so that you can put it firmly into position on a piece of paper. When you draw a circle, the sharp point will stay on the dot where you positioned it. The sharp point must not move.
   • The other leg has a space to insert a pencil. When you draw a circle, you move this leg around in a smooth movement, and the pencil will draw the circle on the page. Always use a sharp pencil.
   

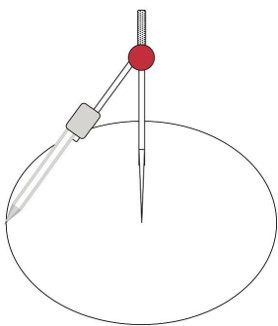
For constructions with a compass, you can either draw a full circle or you can draw short sections of a circle, where needed.

In the diagram below, \(A\) is the centre of the circle and \(BC\) is the diameter of the circle. This means that \(AB\) is a radius of the circle and \(AC\) is also a radius of the circle.

\[AB = AC\]

When we do constructions we seldom draw a complete circle. The solid lines drawn at \(B\) and \(C\) are called arcs.

arc

a part of the circumference of a circle

We will draw arcs in all the constructions that follow.