10.3 Constructing perpendicular lines
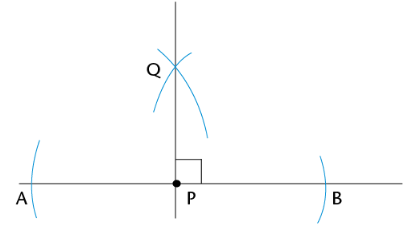
Perpendicular lines intersect at right angles to each other. In the diagram below, \(PQ\) is perpendicular to \(AB\). We use a small square to indicate that the lines intersect at right angles. We use the symbol, \(\perp\), to indicate that two lines are perpendicular to each other. For example, \(AB \perp PQ\).
- perpendicular lines
- lines that intersect at right angles (\(90^{\circ}\)) to each other
The worked example below shows the steps for constructing a perpendicular bisector of a line segment. To bisect a line segment means to divide the line into two equal parts. Later on in this chapter, you will also learn how to bisect an angle. This means to divide a given angle into two equal angles.
- bisect
- to divide into two equal parts
A perpendicular bisector is a line that intersects another line at right angles and divides the second line into two equal parts.
Constructing a perpendicular bisector
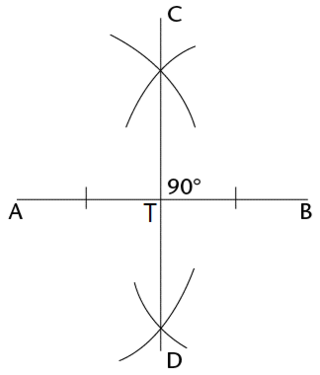
Worked Example 10.1: Constructing a perpendicular bisector of a line segment
- Draw line segment \(AB = 8 \text{ cm}\).
- Construct line \(CD\), the perpendicular bisector of \(AB\). Label the intersection of \(AB\) and \(CD\) as point \(T\).
- Measure \(AT\) and \(TB\). Are they equal?
Draw line segment.
Use a ruler and draw a line. Mark point \(A\) on the line. Make the width of the compass equal to \(8 \text{ cm}\). Place the point of the compass on point \(A\) and mark an arc for point \(B\) on the line. Be as accurate as possible.
Construct two arcs on either side of the line that are the same distance from point \(A\).
Place the point of the compass on point \(A\). Draw arcs above and below the line \(AB\).

Construct two arcs on either side of the line that are the same distance from point \(B\).
Without changing the compass width, place the point of the compass on point \(B\). Draw arcs above and below the line \(AB\). The two arcs above the line should intersect (point \(C\)) as should those below the line (point \(D\)).

Draw line \(CD\) perpendicular to line \(AB\).
Use a ruler to draw the line segment \(CD\).
Use a ruler to measure the length of \(AT\) and \(TB\).
When you measure, you should find that:
\[\begin{align} AT &= 4 \text{ cm} \\ TB &= 4 \text{ cm} \\ \therefore AT &= TB \end{align}\]\(\therefore\ CD\) is the perpendicular bisector of \(AB\).
The symbol \(\therefore\) means “therefore”. It shows that a mathematical statement is a logical next step or conclusion that is true because of the step above.
Constructing a perpendicular line at a given point on the line
Worked Example 10.2: Constructing a perpendicular line at a given point on the line
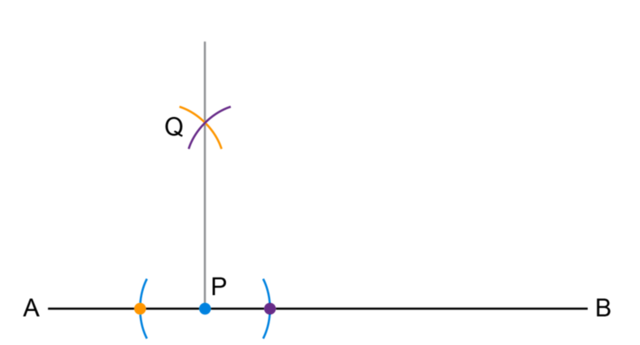
\(P\) is a point on the line \(AB\). Construct line \(PQ\) such that \(AB \perp PQ\).
Draw line \(AB\) with point \(P\) anywhere on line \(AB\).
Construct two arcs that are the same distance from point \(P\).
Place your compass on the point \(P\). Draw an arc across the line \(AB\) on each side of the point \(P\). Make sure to keep the width of the compass exactly the same when drawing both arcs.
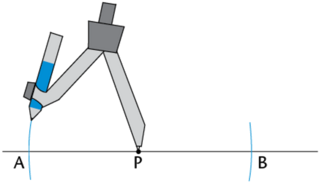
Construct two intersecting arcs above the point \(P\).
Open your compass so that it is wider than the distance \(AP\). Place the compass on point \(A\) and draw an arc above point \(P\).
Keeping the width of the compass the same, place the compass on point \(B\) and draw another arc above point \(P\). Label the point of intersection \(Q\).

Draw line \(PQ\) perpendicular to line \(AB\).
Use your ruler to join the point \(Q\) and point \(P\).
\(PQ\) is perpendicular to \(AB\). We can write this as: \(PQ \perp AB\) or \(AB \perp PQ\). Both statements mean the same thing.
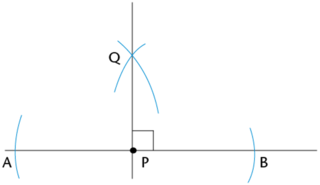
If you have to do a construction involving a line that is not horizontal on the page in front of you, it might be easier to turn your workbook so that the line is horizontal.
Never erase any construction lines after you have completed a construction.
Worked Example 10.3: Constructing a perpendicular line from a given point above the line
Point \(P\) lies above the line \(AB\). Construct line \(PQ\) such that \(AB \perp PQ\).
Construct two arcs on \(AB\) that are the same distance from point \(P\).
Place the point of your compass on the point \(P\). Draw arcs that cut the line on both sides of point \(P\). Make sure to keep the width of the compass exactly the same when drawing the two arcs.
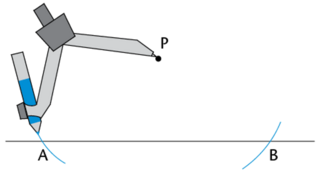
Construct two intersecting arcs below the line \(AB\).
Do not change the width of the compass. Place the point of the compass on point \(A\) and construct an arc below the line. Keeping the width of the compass the same, place the point of the compass on point \(B\) and construct another arc below the line. Label the point of intersection \(Q\).
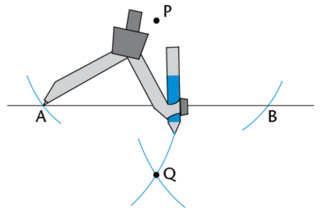
Draw line \(PQ\) perpendicular to line \(AB\).
Use your ruler to draw the line \(PQ\).
\(PQ\) is perpendicular to \(AB\), or \(PQ \perp AB\).
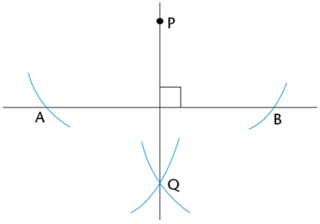
When we construct a perpendicular line from a point above the line, this can also be called dropping a perpendicular line from a given point.
Construct perpendicular lines
Given line segment \(PQ = 6 \text{ cm}\):
- Construct \(ST\), the perpendicular bisector of \(PQ\).
- Label point \(V\), the point of intersection of \(PQ\) and \(ST\).
- Measure the length of \(PV\) and \(VQ\).
Follow these steps to construct a perpendicular line inside a triangle.
- Use a ruler to draw \(\triangle JKL\). Choose any lengths for the sides of \(\triangle JKL\).
- Mark point \(M\) anywhere along the side \(JK\) of \(\triangle JKL\).
- Construct a perpendicular line at point \(M\).
Follow these steps to construct a perpendicular line inside a triangle.
- Use a ruler to draw \(\triangle ABC\). Choose any lengths for the sides of \(\triangle ABC\).
- Use a ruler to measure the length of each side of the triangle. Which is the longest side?
- Mark point \(D\) anywhere inside \(\triangle ABC\).
- Drop a perpendicular line from point \(D\) to the longest side of the \(\triangle ABC\).
Given line segment \(CD = 9 \text{ cm}\):
- Construct \(FG\), the perpendicular bisector of \(CD\).
- Label point \(K\), the point of intersection of \(CD\) and \(FG\).
- Measure and confirm that \(CK = KD\).
Follow these steps to do constructions in a triangle.
- Use a ruler to draw \(\triangle XYZ\). Choose any lengths for the sides of \(\triangle XYZ\). All
the
interior angles must be less than \(90^{\circ}\). An example triangle is shown below.
- Construct the perpendicular bisector of \(XY\).
- Construct the perpendicular bisector of \(YZ\).
- What do you notice about these two lines?
- Do you think that your observation about the perpendicular bisector of \(XY\) and perpendicular bisector of \(YZ\) would also be true for the perpendicular bisector of \(ZX\)?
Tumi used a compass and ruler to complete a geometric construction. Each step of her construction is shown below.
- Study the diagrams. What did Tumi construct?
- Tumi needs help completing her work. Write a short sentence for each diagram describing the method used for each step of the construction. Use your own words and make your sentences as clear and simple as possible.
- Step 1:

- Step 2:

- Step 3:
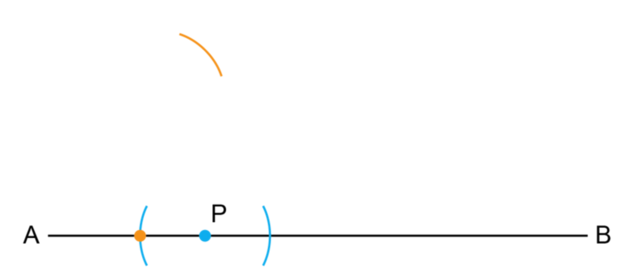
- Step 4:
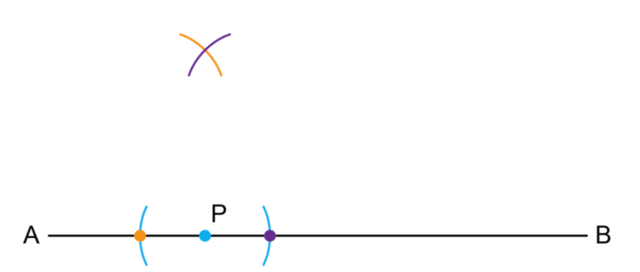
- Step 5: