10.8 Properties of geometric figures
In this section, we will investigate the properties of triangles and quadrilaterals by constructing different types of triangles, including equilateral triangles and isosceles triangles. We will also investigate the properties of different quadrilaterals, including squares, rectangles, rhombuses and parallelograms. For most of our investigations, we will focus on the sum of the interior angles of shapes and some of the special relationships between sides and angles.
Investigating the properties of triangles
Finding the sum of the interior angles of a triangle
- What do you know about the sum of angles on a straight line? Complete the sentence: The sum of angles on a straight line …
- Express your answer to Question 1 mathematically. You can also include a diagram in your answer.
- Use a ruler and a pencil to construct any \(\triangle ABC\). You can choose any length for the sides of the triangle and any angles for the interior angles of the triangle.
Label the interior angles \(\hat{A}, \hat{B}\) and \(\hat{C}\). An example is shown below.
Cut the triangle into three pieces.
Draw a straight line on a piece of paper. Mark a point in the middle of the line. Can you arrange the three vertices of \(\triangle ABC\) at the point on the straight line? An example is shown below.
- What can you deduce about the sum of angles in a triangle? Complete the sentence: The sum of angles in a triangle …
- Express your answer to Question 7 mathematically.
Worked Example 10.17: Calculating the size of a missing angle in a triangle
\(\triangle ABC\) has three angles of different sizes. This means it is a scalene triangle. Calculate the size of \(\hat{B}\) in \(\triangle ABC\).
Write an expression for the sum of angles in a triangle.
We know that the sum of the interior angles of a triangle is equal to \(180^{\circ}\).
\(\hat{A} + \hat{B} + \hat{C} = 180^{\circ}\).
Calculate the size of \(\hat{B}\).
From the information given in the diagram, we know that \(\hat{A} = 81^{\circ}\) and \(\hat{C} = 53^{\circ}\).
So
\[\begin{align} \hat{A} + \hat{B} + \hat{C} &= 180^{\circ} (\text{sum } \angle \text{s in } \triangle) \\ 81^{\circ} + \hat{B} + 53^{\circ} &= 180^{\circ} \\ \hat{B} &= 180^{\circ} − 53^{\circ} − 81^{\circ} \\ \therefore \hat{B} &= 46^{\circ} \end{align}\]Equilateral triangles
An equilateral triangle is a triangle with all sides equal in length. The following activity is an investigation into the interior angles of an equilateral triangle.
- equilateral triangle
- a triangle with all sides equal in length
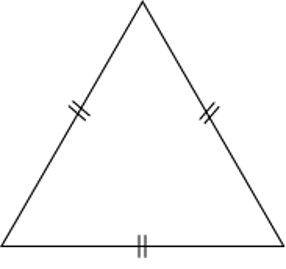
Investigating the interior angles of an equilateral triangle
- What do you know about the sides of an equilateral triangle? Write a short sentence and include a diagram in your answer.
- We have already learned how to construct a triangle given the lengths of all three sides. You might need to go back and revise the method for constructing a triangle given all three sides. Then, construct \(\triangle PQR\) such that \(PQ = QR = RP\). You can choose any length for the sides of the triangle.
- Check the accuracy of your construction by measuring the length of each side of the triangle.
- Use a protractor to measure the size of angles \(\hat{P}\), \(\hat{Q}\) and \(\hat{R}\).
- What do you notice?
- What can you deduce about the interior angles of an equilateral triangle?
- Complete the sentence: The interior angles of an equilateral triangle are … and the size of each angle is \(\ldots^{\circ}\).
- Do you think the following statement is true or false? A triangle with longer sides than \(\triangle PQR\) would have bigger interior angles and a triangle with shorter sides than \(\triangle PQR\) would have smaller interior angles.
Isosceles triangles
An isosceles triangle is a triangle with two equal sides.
- isosceles triangle
- a triangle with two sides that are equal
The diagram below shows isosceles triangle \(\triangle DEF\) with \(DE = FD\).
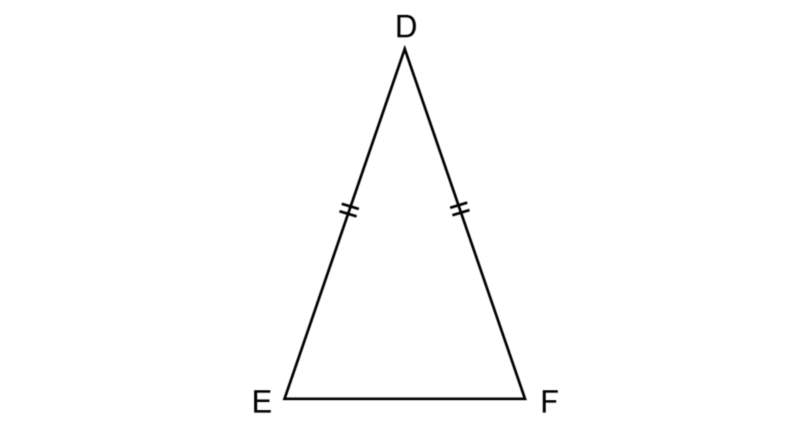
The following activity is an investigation into the interior angles of an isosceles triangle.
Investigating the interior angles of an isosceles triangle
- Use a ruler and a compass to complete the steps for constructing isosceles triangle \(\triangle TRS\).
- Draw a line segment and mark points \(T\) and \(R\) on the line. \(TR\) is the base of the triangle. You can choose any length for \(TR\).
- Set the width of the compass to be wider than the midpoint of \(TR\). Place the compass on \(T\) and make an arc above the line \(TR\).
- Keeping the width of the compass the same, place the compass on point \(R\) and draw an arc that
intersects the other arc. Label the point \(S\).
- Draw sides \(RS\) and \(ST\).
- Use a ruler to measure the length of each side of \(\triangle TRS\).
- \(TR = …\)
- \(RS = …\)
- \(ST = …\)
- Use a protractor to measure the size of each interior angle of \(\triangle TRS\):
- \(\hat{T} = …\)
- \(\hat{R} = …\)
- \(\hat{S} = …\)
- What do you notice about the base angles of \(\triangle TRS\)?
- Complete the sentence: If a triangle has two sides of equal length, then it is called an …. triangle and the base angles of the triangle are …
- Complete the following expression: \(\hat{T} + \hat{R} + \hat{S} = …\)
Worked Example 10.18: Calculating the interior angles of an isosceles triangle
The diagram shows isosceles triangle \(\triangle ABC\) with \(AC = BC\). Determine the values of \(y\) and \(x\), giving reasons for your answer.
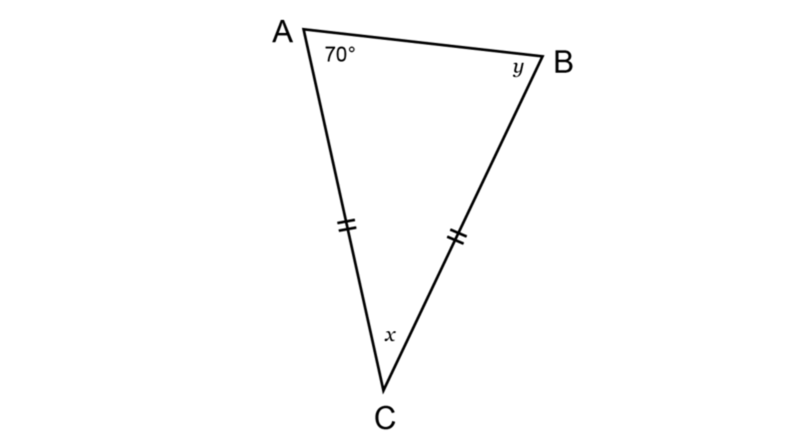
Use the given information to find the value of \(y\).
The information on the diagram shows that \(BC = AC\). We know that the base angles of an isosceles triangle are equal (reason: angles opposite equal sides).
So, \(C\hat{A}B = C\hat{B}A\).

Determine the value of \(x\).
The sum of the interior angles of a triangle is \(180^{\circ}\).
\[\begin{align} \hat{A} + \hat{B} + \hat{C} &= 180^{\circ} (\angle \text{ sum in } \triangle) \\ x + 70^{\circ} + 70^{\circ} &= 180^{\circ} \\ x + 140^{\circ} &= 180^{\circ} \\ x &= 180^{\circ} − 140^{\circ} \\ x &= 40^{\circ} \end{align}\]Check your solution.
A quick calculation will show that the sum of the three interior angles of \(\triangle ABC\) adds up to \(180^{\circ}\).
\[\begin{align} \hat{A} + \hat{B} + \hat{C} &= 180^{\circ} \\ 40^{\circ} + 70^{\circ} + 70^{\circ} &= 180^{\circ} \end{align}\]Investigating properties of quadrilaterals
Finding the sum of the interior angles of a quadrilateral.
- What do you know about the sum of angles in a triangle? Complete the sentence: The sum of angles in a triangle …
- Express your answer to question 1 mathematically. You can also include a diagram in your answer.
- Use a ruler and a pencil to construct quadrilateral \(MNPQ\). You can choose any lengths for the sides of
the quadrilateral. Label the vertices of \(MNPQ\).
An example is shown below. Do not copy this shape, draw your own quadrilateral.
- Complete the sentence: The sum of the interior angles of \(MNPQ = \hat{M} + … + … + …\)
- Draw diagonal \(MP\).
- What do you notice? Name the two shapes that are formed by diagonal \(MP\).
- What do you know about the sum of the interior angles of this shape?
- Complete the following: Sum of interior angles of \(MNPQ\) = \(2\) \(\times\) sum of interior angles of a .. = \(2 \times …^{\circ}\) = \(…^{\circ}\)
- What can you deduce about the sum of the interior angles of a quadrilateral?
- Complete the sentence: The sum of the interior angles of a quadrilateral is equal to \(\ldots^{\circ}\).
Opposite sides and angles of a parallelogram
- Use a ruler and a compass to complete the steps for constructing parallelogram \(ABCD\).
- Draw a line segment and mark points \(A\) and \(B\) on the line. \(AB\) is one side of parallelogram \(ABCD\).
- At point \(A\), draw a line segment at any angle to side \(AB\) and mark point \(D\) on the line. \(AD\)
is the side of parallelogram \(ABCD\) adjacent to \(AB\).
- Set the width of the compass to be narrower than \(AD\). Place the compass on \(A\) and make a wide arc that cuts \(AB\) and \(AD\).
- Keeping the width of the compass the same, place the compass on \(D\) and draw a wide arc that cuts the line above point \(D\).
- Set the width of the compass to the length \(FG\) (green dotted line). Keeping the width of the compass
the same, place the compass on the point where the arc cuts the line above \(D\). Make an arc that cuts the
other arc.
- Construct a line through the point of intersection and point \(D\) and parallel to side \(AB\).
- Set the width of the compass to the length \(AG\). Keeping the width of the compass the same, place the compass on \(B\) and make a wide arc that cuts the line \(AB\) to the right of \(B\).
- Set the width of the compass to the length \(FG\). Keeping the width of the compass the same, place the compass on the point where the arc cuts the line to the right of \(B\). Make an arc that cuts the other arc.
- Construct a line through the point of intersection and point \(B\) and parallel to side \(AD\).
- Label the point of intersection of the two lines, point \(C\).
- Use a ruler to measure the lengths of the sides:
- \(AB = …\)
- \(BC = …\)
- \(CD = …\)
- \(DA = …\)
- What do you notice about opposite sides of a parallelogram?
- Use a protractor to measure the size of the interior angles:
- \(\hat{A} = …\)
- \(\hat{B} = …\)
- \(\hat{C} = …\)
- \(\hat{D} = …\)
- What do you notice about opposite angles of a parallelogram?
- Complete the expression: The sum of the interior angles of \(ABCD = … + … + … + … = …^{\circ}\).
Worked Example 10.19: Calculating interior angles of a quadrilateral
In quadrilateral \(QRST\), \(\hat{R} = 110^{\circ}, \hat{S} = 104^{\circ}\) and \(\hat{T} = 47^{\circ}\).
Find the value of \(x\), giving a reason for your answer.
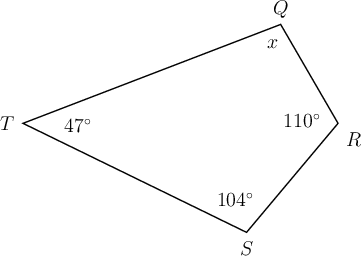
Use what you know about the interior angles of a quadrilateral.
For any quadrilateral, the sum of the interior angles \(= 2 \times 180^{\circ} = 360^{\circ}\).
In quadrilateral \(QRST\), \(\hat{Q} + \hat{R} + \hat{S} + \hat{T} = 360^{\circ}\).
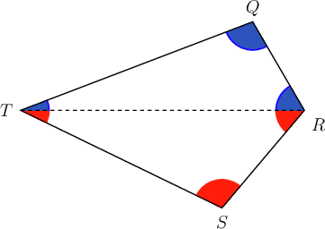
Determine the values of \(x\).
\[\begin{align} \hat{Q} + \hat{R} + \hat{S} + \hat{T} &= 360^{\circ} (\text{sum of } \angle \text{s in quad}) \\ x + 110^{\circ} + 104^{\circ} + 47^{\circ} &= 360^{\circ} \\ x &= 360^{\circ} − 261^{\circ} \\ x &= 99^{\circ} \end{align}\]Check your answer
A quick calculation will show that the sum of the interior angles of \(QRST\) adds up to \(360^{\circ}\).
\[\begin{align} \hat{Q} + \hat{R} + \hat{S} + \hat{T} &= 360^{\circ} \\ 110^{\circ} + 104^{\circ} + 47^{\circ} + 99^{\circ} &= 360^{\circ} \end{align}\]Properties of parallelograms
- A parallelogram has two pairs of opposite sides that are equal and parallel.
- The interior opposite angles of a parallelogram are equal.
- Opposite sides are equal.
- Opposite sides are parallel.
- Opposite angles are equal.
