14.5 Solving problems
Worked Example 14.9: Working with money
Two friends reach into their pockets and pull out the change they have. Ahmed has \(\text{R}\,\text{2,25}\) and Sujatha has \(\text{R}\,\text{2,55}\). Who has more money? Which amount is larger?
Use your knowledge to find the answer.
We have two numbers, and we must decide which of them is bigger: \(\text{R}\,\text{2,25}\) or \(\text{R}\,\text{2,55}\). Your experience with money probably helps you understand which number is bigger, and who has more money!
Use a number line to check your answer.
It is also helpful to mark the numbers on the number line. The number \(\text{2,25}\) sits exactly in the middle of \(\text{2,2}\) and \(\text{2,3}\). Remember that \(\text{2,2} = \text{2,20}\) and \(\text{2,3} = \text{2,30}\) and between them are these ten numbers: \(\text{2,21}\) and \(\text{2,22}\) and \(\text{2,23}\) and so on, up to \(\text{2,29}\) and then \(\text{2,30}\).
\(\text{2,25}\) is in the middle of these ten divisions. You can see this on the number line below.
The number \(\text{2,55}\) sits in the middle of \(\text{2,50}\) and \(\text{2,60}\).
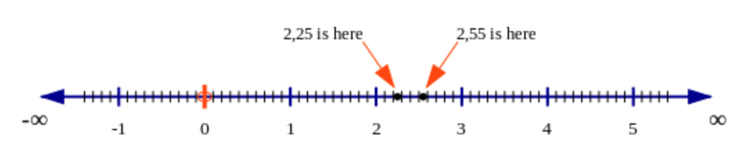
For two numbers on the number line, the one on the right is always greater than the one on the left. Therefore, \(\text{2,55}\) must be the bigger number. This makes sense because \(\text{R}\,\text{2,55}\) is more money than \(\text{R}\,\text{2,25}\).
Remember that the inequality symbol always opens to the larger number, like a creature eating the larger snack! It is like this:
Therefore, the correct answer is: Sujatha has more money because \(\text{R}\,\text{2,25} < \text{R}\,\text{2,55}\). (In words, the inequality means, “\(\text{R}\,\text{2,25}\) is less than \(\text{R}\,\text{2,55}\)”.)
You will see decimal numbers in calculations with different measurements. For example, when calculating the perimeter or area of a shape, the side measurements could be given in decimal notation.
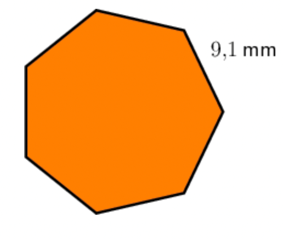
The side of this regular heptagon is \(\text{9,1} \text{ mm}\). To find its perimeter, you need to add all the sides or multiply the \(\text{9,1} \text{ mm}\) side length by \(7\):
If we walk all the way around the shape we walk \(\text{9,1} \text{ mm}\) seven times, so
\[\begin{align} P &= 7 \times \text{9,1} \\ &= \text{63,7} \text{ mm} \end{align}\]Worked Example 14.10 Calculating area with decimals
Consider the following rectangle.
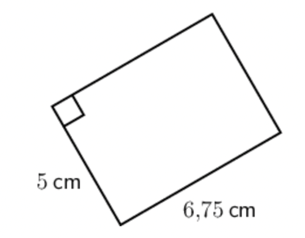
- Determine the perimeter of the rectangle and select the correct unit.
- Determine the area of the rectangle and select the correct unit.
Determine the perimeter by adding all the sides.
To find the perimeter of a polygon, we add up all of the sides as if we are walking around the edge of the shape. Perimeter is a distance, so it is measured in units of length (such as centimetres, metres or kilometres).
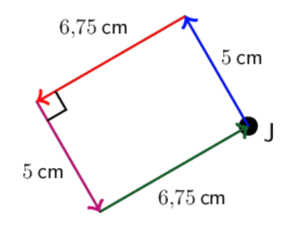
If we start at Point J and walk around the shape, we get
\[\begin{align} P &= 5 + \text{6,75} + 5 + \text{6,75} \\ &= \text{23,5} \text{ cm} \end{align}\]The opposite sides of a rectangle are the same length. If we let one side be \(l\) and the other side be \(b\), then the perimeter is
\[\begin{align} P &= l + b + l + b \\ &= 2l + 2b \end{align}\]
Determine the area by calculating the number of square centimetres taken up by the shape.
To calculate the area of the rectangle, we must work out how many square centimetres (\(\text{cm}^{2}\)) will fit in the space.
We use the formula for area of a rectangle:
\[\begin{align} A &= l \times b \\ &= 5 \times \text{6,75} \\ &= \text{33,75} \text{ cm}^{2} \end{align}\]
