To write these algebraic products in exponential form, we count the number of times a variable is multiplied by itself in each expression.
\[x \times x \times x \times x \times x \times x \times x \times x = x^{8}\]3.4 Calculations using numbers in exponential form: Laws of exponents
Now that you know how to work with whole numbers and integers when using exponents, you can learn to use the algebraic rules for exponents.
The exponential form \(a^{b}\) is read as “\(a\) to the power of \(b\)”, where \(a\) is called the base and \(b\) is called the exponent or index. The number at \(b\) indicates the number of factors that are multiplied.
For example, \(a^{3} = a \times a \times a\) and \(a^{6} = a \times a \times a \times a \times a \times a\).
Product of powers
Suppose we are asked to simplify \(3^{2} \times 3^{4}\). We can do this calculation in two different ways: We can calculate each exponent and then multiply the answers, or we can use a special rule, the product of powers.
Let’s see how the solution works.
\[3^{2} \times 3^{4} = (3 \times 3) \times (3 \times 3 \times 3 \times 3)\] \[= 9 \times 81\] \[= 729\] \[= 3^{6}\]There are \(2\) factors of \(3\) in \(3^{2}\), and there are \(4\) factors of \(3\) in \(3^{4}\).
The base (\(3\)) is a repeated factor. The exponents (\(2\) and \(4\)) tell us the number of times each factor is repeated.
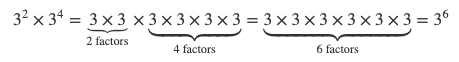
So, \(3^{2} \times 3^{4} = 3^{2 + 4}\).
The product of powers rule states that when you multiply two or more powers that have the same base, the answer has the same base, but its exponent is equal to the sum of the exponents of the numbers you are multiplying.
We can express this algebraically as \(a^{m} \times a^{n} = a^{m + n}\), where \(m\) and \(n\) are natural numbers and \(a\) is not zero. We write these conditions as \(m\) \(\mathbb{\in N,\ }\) \(n\) \(\mathbb{\in N}\) and \(a \neq 0\).
- product of powers rule
- \(a^{m} \times a^{n} = a^{m + n}\); \(m\) \(\mathbb{\in N,\ }\) \(n\) \(\mathbb{\in N}\) and \(a \neq 0\).
Remember, \(a^{1} = a\) and \(1^{a} = 1\).
Any number raised to a power \(1\) is equal to the number itself.
The number \(1\) raised to any power is equal to \(1\).
For example, \(1\ 000^{1} = 1\ 000\), and \(1^{1\ 000} = 1\).
Write each of the following products in exponential form.
\((a \times a \times a \times a) \times (a \times a \times a) \times (a \times a) \times a^{1}\) \(= (a^{4}) \times (a^{3}) \times (a^{2}) \times a^{1}\) \(= a^{4 + 3 + 2 + 1}\) \(= a^{10}\)
Simplify the following expressions. Give your answer with an exponent, for example: \(2^{5}\).
Use the product of powers rule to simplify these numeric expressions. Remember to apply this rule only to the exponents that have the same bases.
\[3^{9} \times 3^{2} = 3^{9 + 2} = 3^{11}\]Simplify the expressions. Your answer should include an exponent.
- \[x^{9} \times {x}^2\]
- \[y^{4} \times y^{6}\]
- \[a^{3} \times a^{4} \times a^{5}\]
- \[b^{3} \times c^{4} \times b^{4} \times c^{6}\]
When working with variables as bases, the product of power rule works the same way.
- \[x^{9} \times x^{2} = x^{9 + 2} = x^{11}\]
- \[y^{4} \times y^{6} = y^{4 + 6} = y^{10}\]
- \[a^{3} \times a^{4} \times a^{5} = a^{3 + 4 + 5} = a^{12}\]
- \[b^{3} \times c^{4} \times b^{4} \times c^{6}\] \[= (b^{3} \times b^{4}) \times (c^{4} \times c^{6})\] \[= b^{3 + 4} \times c^{4 + 6}\] \[= b^{7} \times c^{10}\] \[= b^{7}c^{10}\]
Quotient of powers
Suppose we are asked to divide \(5^{6} \div 5^{3}\).
We can expand each power and see what happens:
\[5^{6} \div 5^{2} = (5 \times 5 \times 5 \times 5 \times 5 \times 5) \div (5 \times 5)\] \[= \frac{5 \times 5 \times 5 \times 5 \times \mathbf{5 \times 5}}{\mathbf{5 \times 5}}\] \[=5 \times 5 \times 5 \times 5\] \[= 5^{4}\] \[= 5^{6 - 2}\]The quotient of powers rule states that when you divide powers with the same base, the answer has the same base, but its exponent is equal to the difference of the exponents of the numbers you are dividing.
We can express this algebraically as \(a^{m} \div a^{n} = a^{m - n}\), where \(m\) and \(n\) are natural numbers and \(a\) is not zero (\(m\) \(\mathbb{\in N,\ }\) \(n\) \(\mathbb{\in N}\) and \(a \neq 0\)).
- quotient of powers rule
- \(a^{m} \div a^{n} = a^{m - n}\); \(m\) \(\mathbb{\in N,\ }\) \(n\) \(\mathbb{\in N}\) and \(a \neq 0\).
Simplify the following. Do not use a calculator.
- \[\frac{3^{17}}{3^{12}}\]
- \[6^{17} \div 6^{14}\]
- \[5^{7} \div 5\]
- \[10^{20} \div 10^{20}\]
Remember, when we divide the same bases, we subtract the exponents.
- \[\frac{3^{17}}{3^{12}} = 3^{17 - 12} = 3^{5} = 243\]
- \[6^{17} \div 6^{14} = 6^{17 - 14} = 6^{3} = 216\]
- \(5^{7} \div 5 = 5^{7 - 1} = 5^{6}\)
Be careful: \(5 = 5^{1}\), but \(5 \neq 5^{0}\)! - \[10^{20} \div 10^{20} = 10^{20 - 20} = 10^{0} = 1\]
Simplify.
- \[x^{7} \div x^{5}\]
- \[y^{11} \div y^{8}\]
- \[\frac{t^{21}}{t^{15}}\]
- \[n^{11} \div n^{8} \div n^{3}\]
- \[x^{7} \div x^{5} = x^{7 - 5} = x^{2}\]
- \[y^{11} \div y^{8} = y^{11 - 8} = y^{3}\]
- \[\frac{t^{21}}{t^{15}} = t^{21 - 15} = t^{6}\]
- \[n^{11} \div n^{8} \div n^{3} = n^{11 - 8} \div n^{3} = n^{3} \div n^{3} = n^{3 - 3} = n^{0} = 1\]
Raising a power to a power
Suppose we are asked to simplify \(\left( 3^{2} \right)^{4}\). We can also do this calculation in two different ways: We can calculate inside the brackets and then raise the answer to another power, or we can use a special rule – the raising a power to another power rule.
Let’s see how the solution works.
\[\left( 3^{2} \right)^{4} = (3 \times 3) \times \left( 3 \times 3) \times (3 \times 3 \right) \times (3 \times 3)\] \[= 3^{8}\]There are \(2\) factors of \(3\) in \(3^{2}\), and there are \(2 \times 4 = 8\) factors of \(3\) in \(\left( 3^{2} \right)^{4}\).
So, to simplify \(\left( x^{2} \right)^{5}\) we can write it out as a product of powers, or we can use a shortcut.
\[\left( x^{2} \right)^{5} = \left( x^{2} \right) \times \left( x^{2} \right) \times \left( x^{2} \right) \times \left( x^{2} \right) \times \left( x^{2} \right)\] \[= (x \times x) \times (x \times x) \times (x \times x) \times (x \times x) \times (x \times x)\] \[= x^{10}\]\(2 \times 5 = 10\) factors
The raising a power to a power rule states that when a base is raised to more than one power, the powers are multiplied.
We can express this algebraically:
\(a^{m} \div a^{n} = a^{m - n}\); \(m\) \(\mathbb{\in N,}\) \(n\) \(\mathbb{\in N}\) and \(a \neq 0\).
- raising a power to a power rule
- \(a^{m} \div a^{n} = a{m - n}\); \(m\) \(\mathbb{\in N,}\) \(n\) \(\mathbb{\in N}\) and \(a \neq 0\).
Simplify.
- \[\left( 5^{4} \right)^{10}\]
- \[\left( 10^{4} \right)^{5}\]
- \[\left( 6^{4} \right)^{4}\]
- \[\left( x^{2} \right)^{5}\]
We can use the rule and multiply the powers.
- \[\left( 5^{4} \right)^{10} = 5^{4 \times 10} = 5^{40}\]
- \[\left( 10^{4} \right)^{5} = 10^{4 \times 5} = 10^{20}\]
- \[\left( 6^{4} \right)^{4} = 6^{4 \times 4} = 6^{16}\]
- \[\left( x^{2} \right)^{5} = x^{2 \times 5} = x^{10}\]
Write \(5^{15}\) as a power of \(5\) in two different ways.
To write \(5^{15}\) as a power of \(5\), we need to find the second factor of \(15\).
\[15 = 5 \times \mathbf{3}\]So, \(5^{15}=5^{5×3}=(5^{5})^{3}\) or \(5^{15}=(5^{3})^{5}\)
Power of a product
\(12^{2}\) can be written in terms of its factors as \((2 \times 6)^{2}\) or as \((3 \times 4)^{2}\).
We already know that \(12^{2} = 144\).
What this tells us is that both \((2 \times 6)^{2}\) and \((3 \times 4)^{2}\) also equal to \(144\).
We write \(12^{2}\):
\[12^{2} = (2 \times 6)^{2} = 2^{2} \times 6^{2} = 4 \times 36 = 144\]or
\[12^{2} = (3 \times 4)^{2} = 3^{2} \times 4^{2} = 9 \times 16 = 144\]A product raised to a power is the product of the factors, with each raised to the same power. Therefore, the power of a product rule, in algebraic notation, is \((a \times b)^{m} = a^{m} \times b^{m}\); \(m\) \(\mathbb{\in N}\), \(a≠0\) and \(b≠0\).
- power of a product rule
- \((a \times b)^{m} = a^{m} \times b^{m}\); \(m\) \(\mathbb{\in N}\), \(a≠0\) and \(b≠0\).
Write each exponent as a product of two exponents.
- \[(5 \times 2)^{4}\]
- \[(9)^{7}\]
- \[(7 \times 100)^{3}\]
- \[(2\ 000)^{2}\]
Use the power of a product rule.
- \[(5 \times 2)^{4} = 5^{4} \times 2^{4}\]
- \[(9)^{7} = (3 \times 3)^{7} = 3^{7} \times 3^{7}\]
- \[(7 \times 100)^{3} = 7^{3} \times 100^{3}\]
- \[(2\ 000)^{2} = (2 \times 1\ 000)^{2} = 2^{2} \times {1\ 000}^{2}\]
You can write \({2\ 000}^{2}\) as a product of different factors.
Write each of the following expressions with one base.
- \[3^{2} \times 5^{2}\]
- \[5^{3} \times 2^{3}\]
- \[7^{4} \times 4^{4}\]
- \[2^{3} \times 6^{3}\]
The exponents are the same, so we can use the rule.
- \[3^{2} \times 5^{2} = (3 \times 5)^{2} = 15^{2}\]
- \[5^{3} \times 2^{3} = (5 \times 2)^{3} = 10^{3}\]
- \[7^{4} \times 4^{4} = (7 \times 4)^{4} = 28^{4}\]
- \[2^{3} \times 6^{3} = (2 \times 6)^{3} = 12^{3}\]
To multiply the bases of the powers, the exponents need to be the same.
\(3^{2} \times 5^{2} = (3 \times 5)^{2}\)
\(3^{2} \times 5^{3} \neq (3 \times 5)^{6}\)
Simplify the following expressions.
- \[(2x)^{3}\]
- \[(xy)^{4}\]
- \[(5y)^{2}\]
- \[(6b)^{3}\]
When simplifying algebraic expressions that have a number as a coefficient, we can calculate the value of the number to simplify the expression further.
- \[(2x)^{3} = 2^{3}x^{3} = 8x^{3}\]
- \[(xy)^{4} = x^{4}y^{4}\]
- \[(5y)^{2} = 5^{2}y^{2} = 25y^{2}\]
- \[(6b)^{3} = 6^{3}b^{3} = 216b^{3}\]
Mixed calculations
Whenever you work out an expression, you must follow the order of operations, BODMAS. However, we need to include exponents!
With exponents, BODMAS becomes BOEDMAS:
- BO ⟶ Do all operations inside of brackets first; leave the operations outside of the brackets until later.
- E ⟶ Do any exponents; exponents always come before multiplication and division!
- DM ⟶ Do division and multiplication from left to right; division does not always come before multiplication.
- AS ⟶ Do addition and subtraction from left to right; addition does not always come before subtraction.
It is therefore helpful to think of the order of operations with exponents in four pieces:
BO-E-DM-AS
Now let’s work out the value of this expression: \(5^{2} + 14\). The expression includes an exponent and addition. The first calculation we do must be the exponent part, \(5^{2}\). Then we will do the addition.
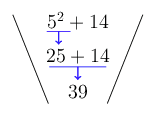
Your working should look like this. The steps are highlighted by the blue underline and arrow.
Notice how the numbers come down, and the working is like the shape of a funnel. It is very important to organise your work like this: it will help you avoid mistakes!
The correct answer is \(5^{2} + 14 = 39\).
Simplify the following:
- \[3^{3} + \sqrt[3]{- 27} \times 2\]
- \[5 \times (2 + 3)^{2} + ( - 1)^{0}\]
- \[3^{2} \times 2^{3} + 5\ \times \ \sqrt{100}\]
- \[\frac{\sqrt[3]{1\ 000}}{\sqrt{100}} + (4 - 1)^{2}\]
- \[\sqrt{16}\ \times \ \sqrt{16} + \sqrt[3]{216} + 3^{2} \times 10\]
- \[4^{3} \div 2^{3} + \sqrt{144}\]
Remember to follow the order of operations.
- \[\begin{align*} & 3^{3} + \sqrt[3]{- 27} \times 2 \\ &= 3^{3} + ( - 3) \times 2 \\ &= 27 - 6 \\ &= 21 \end{align*}\]
- \[\begin{align*} & 5 \times (2 + 3)^{2} + ( - 1)^{0} \\ &= 5 \times 5^{2} + 1 \\ &= 5^{3} + 1 \\ &= 125 + 1 \\ &= 126 \end{align*}\]
- \[\begin{align*} & 3^{2} \times 2^{3} + 5 \times \sqrt{100} \\ &= 9 \times 8 + 5 \times 10 \\ &= 72 + 50 \\ &= 122 \end{align*}\]
- \[\begin{align*} & \frac{\sqrt[3]{1\ 000}}{\sqrt{100}} + (4 - 1)^{2} \\ &= \frac{10}{10} + 3^{2} \\ &= 1 + 9 \\ &= 10 \end{align*}\]
- \[\begin{align*} & \sqrt{16} \times \sqrt{16} + \sqrt[3]{216} + 3^{2} \times 10 \\ &= 4 \times 4 + 6 + 90 \\ &= 16 + 6 + 90 \\ &= 112 \end{align*}\]
- \[\begin{align*} & 4^{3} \div 2^{3} + \sqrt{144} \\ &= \frac{\left( 2^{2} \right)^{3}}{2^{3}} + 12 \\ &= \frac{2^{6}}{2^{3}} + 12 \\ &= 2^{3} + 12 \\ &= 8 + 12 \\ &= 20 \end{align*}\]
